Уравнение первого закона термодинамики для потока
Рисунок 2-6
Рассмотрим уравнение первого закона термодинамики (2-15а):
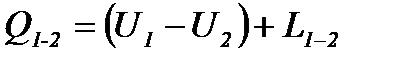
Здесь индексы 1 и 2 относим к двум сечениям потока (рис.2-6). Проанализируем, из чего складывается для потока фигурирующая в этом уравнении величина 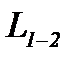 ; для этого выясним, какие виды работы производит движущийся поток газа (жидкости).
; для этого выясним, какие виды работы производит движущийся поток газа (жидкости).
Итак, рассмотрим поток в канале произвольной формы (см. рис. 2-6). Между сечениями 1 и 2 может быть подведено некоторое количество тепла 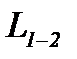 .
.
Площадь сечения 1 канала обозначим через 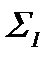 , а сечения 2 – через
, а сечения 2 – через 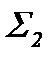 . Давления, которые имеет движущееся вещество в сечениях 1 и 2, обозначим соответственно через
. Давления, которые имеет движущееся вещество в сечениях 1 и 2, обозначим соответственно через 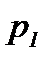 и
и 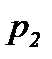 . Количество вещества, проходящего через поперечное сечение потока в единицу времени (массовый расход), обозначим через
. Количество вещества, проходящего через поперечное сечение потока в единицу времени (массовый расход), обозначим через 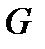 . Безразлично, какое сечение выбрать для измерения расхода
. Безразлично, какое сечение выбрать для измерения расхода 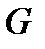 : в соответствии с известным из гидравлики принципом неразрывности потока массовый расход стационарного потока одинаков для любого сечения канала (
: в соответствии с известным из гидравлики принципом неразрывности потока массовый расход стационарного потока одинаков для любого сечения канала ( 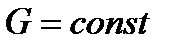 ).
).
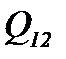 - тепло, сообщенное телу при нагревании от состояния 1 до 2
- тепло, сообщенное телу при нагревании от состояния 1 до 2
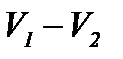 - изменение внутренней энергии тела от 1 до 2
- изменение внутренней энергии тела от 1 до 2
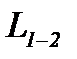 - работа, совершаемая телом в процессе 1-2.
- работа, совершаемая телом в процессе 1-2.
Определим работу, совершаемую потоком.
Для того чтобы ввести в рассматриваемый участок канала через сечение 1 в единицу времени порцию газа (жидкости) массой 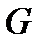 , нужно затратить некоторую работу, расходуемую на то, чтобы вытолкнуть из рассматриваемого участка канала такую же порцию газа и освободить тем самым место для поступающей новой порции газа. Обозначим через
, нужно затратить некоторую работу, расходуемую на то, чтобы вытолкнуть из рассматриваемого участка канала такую же порцию газа и освободить тем самым место для поступающей новой порции газа. Обозначим через  длину пути, проходимого рассматриваемой порцией газа за единицу времени через сечение
длину пути, проходимого рассматриваемой порцией газа за единицу времени через сечение 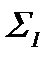 . Сечение этой порции газа можно для наглядности представить себе перемещающимися без трения поршнем (поскольку сечение канала в общем случае переменно, то условный поршень должен иметь изменяющееся сечение; эта условность никак не влияет на получаемые результаты). Для того чтобы переместить этот поршень на расстояние
. Сечение этой порции газа можно для наглядности представить себе перемещающимися без трения поршнем (поскольку сечение канала в общем случае переменно, то условный поршень должен иметь изменяющееся сечение; эта условность никак не влияет на получаемые результаты). Для того чтобы переместить этот поршень на расстояние  , нужно совершить работу, равную произведению силы, действующей на поршень (эта сила равна произведению давления газа
, нужно совершить работу, равную произведению силы, действующей на поршень (эта сила равна произведению давления газа 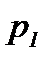 на площадь сечения поршня
на площадь сечения поршня 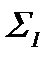 ), на длину пути, пройденного поршнем за единицу времени:
), на длину пути, пройденного поршнем за единицу времени:
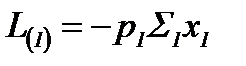
Обозначим:
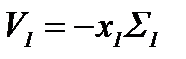 ,
,
где 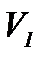 - объем газа, поступившего в рассматриваемый участок канала за единицу времени. Очевидно, что
- объем газа, поступившего в рассматриваемый участок канала за единицу времени. Очевидно, что
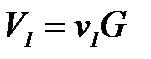 ,
,
где 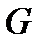 - массовый расход газа в канале,
- массовый расход газа в канале, 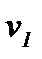 - удельный объем газа в сечении 1.
- удельный объем газа в сечении 1.
Таким образом,
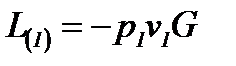 (2-57)
(2-57)
Заметим, что 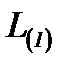 - работа, производимая над потоком, и поэтому величина
- работа, производимая над потоком, и поэтому величина 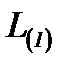 считается отрицательной [знак минус в (2-57)].
считается отрицательной [знак минус в (2-57)].
Работа, которую производит, перемещаясь, поршень, помещенный в сечение 2, подсчитывается аналогичным образом:
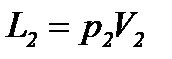 .
.
В соответствии со сформулированным выше принципом неразрывности потока массовый расход газа через сечение 2 тот же, что и через сечение 1, поэтому
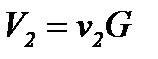
и
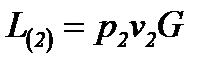 (2-58)
(2-58)
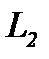 - это работа, которую производит поток (поршень 2), выходящий из сечения 2. Следовательно, эта работа считается положительной.
- это работа, которую производит поток (поршень 2), выходящий из сечения 2. Следовательно, эта работа считается положительной.
Из (2-57) и (2-58) следует, что при протекании газа с расходом 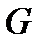 через участок канала между произвольно выбранными сечениями 1 и 2 за единицу времени совершается работа, равная алгебраической сумме работы
через участок канала между произвольно выбранными сечениями 1 и 2 за единицу времени совершается работа, равная алгебраической сумме работы 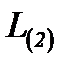 , которую производит поршень 2, и работы
, которую производит поршень 2, и работы 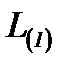 , которая производится над поршнем 1 (эта работа носит название работы проталкивания),
, которая производится над поршнем 1 (эта работа носит название работы проталкивания),
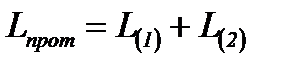 ,
,
откуда в соответствии с (2-57) и (2-58) имеем:
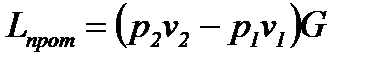 . (2-59)
. (2-59)
Работа проталкивания – это первая часть работы, которую совершает поток.
Далее, если скорость потока в сечении 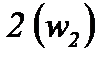 отличается от скорости в сечении
отличается от скорости в сечении  , то для изменения кинетической энергии потока, определяемого соотношением (2-56), также должна быть сообщена (или отобрана) энергия
, то для изменения кинетической энергии потока, определяемого соотношением (2-56), также должна быть сообщена (или отобрана) энергия
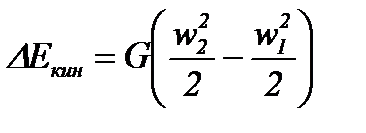 .
.
Это - вторая составная часть работы, совершаемой потоком. Если сечения 1 и 2 расположены на разной высоте (соответственно 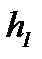 и
и 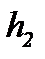 ), то должна быть затрачена работа для того, чтобы поднять рассматриваемую порцию газа с высоты
), то должна быть затрачена работа для того, чтобы поднять рассматриваемую порцию газа с высоты 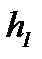 на высоту
на высоту  . Эта работа равна изменению потенциальной энергии порции газа массой
. Эта работа равна изменению потенциальной энергии порции газа массой 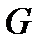 ; в соответствии с (2-12)
; в соответствии с (2-12)
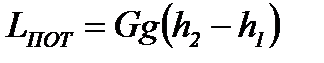 .
.
Это третья составная часть работы, совершаемой потоком.
Следовательно, работа, которую совершает движущийся поток газа (жидкости) в общем случае записывается следующим образом:
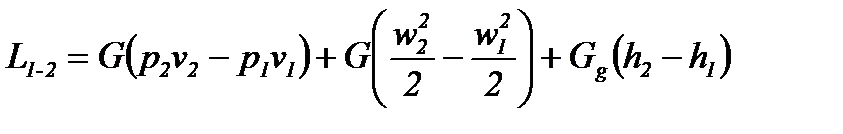 (2-60)
(2-60)
Подставляя соотношение, полученное для величины 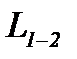 , в уравнение первого закона термодинамики (2-15а), получаем:
, в уравнение первого закона термодинамики (2-15а), получаем:
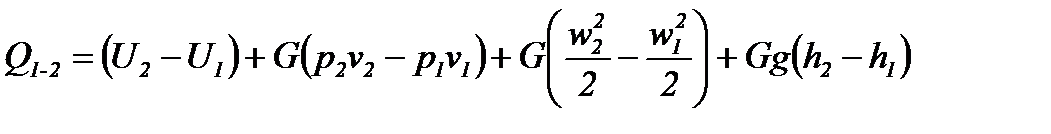 (2-61)
(2-61)
Деля обе части этого уравнения на G, получаем это же соотношение для единицы массы потока (т.е. в удельных массовых величинах):
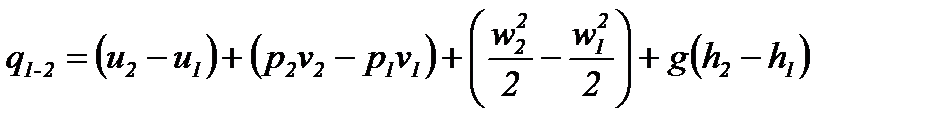 (2-62)
(2-62)
В дифференциальной форме это уравнение запишется в виде
 (2-63)
(2-63)
С учетом того что
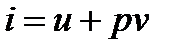 ,
,
получаем
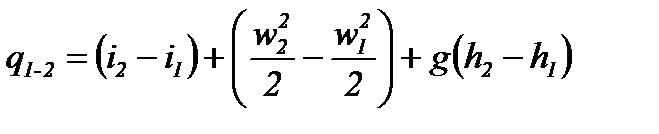 (2-64)
(2-64)
и
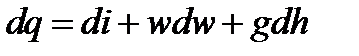 (2-65)
(2-65)
Уравнения (2-64) и (2-65) представляют собой запись первого закона термодинамики для потока.
Сравним теперь дифференциальное уравнение первого закона термодинамики, записанное в самом общем виде для произвольной системы, с частным случаем этого уравнения для потока. Первое из этих уравнений – уравнение (2-23):
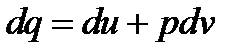 ,
,
второе – уравнение (2-63)
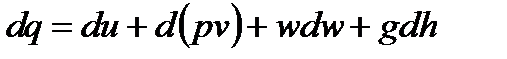
По своему существу уравнения (2-23) и (2-63) идентичны – они выражают первый закон термодинамики. На этом основании можно приравнять правые части этих уравнений. Тогда
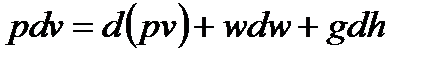 (2-69)
(2-69)
Это соотношение показывает, что работа, расходуемая на проталкивание потока 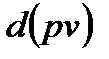 , на изменение кинетической энергии потока,
, на изменение кинетической энергии потока, 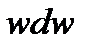 , на изменение потенциальной энергии потока
, на изменение потенциальной энергии потока 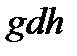 , на преодоление сил трения
, на преодоление сил трения 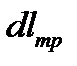 , и техническая работа
, и техническая работа 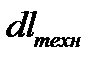 совершается за счет работы расширения газа (или жидкости), движущегося в потоке,
совершается за счет работы расширения газа (или жидкости), движущегося в потоке, 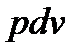 . Это и понятно: если газ в потоке расширяется (т.е. возрастает его удельный объем
. Это и понятно: если газ в потоке расширяется (т.е. возрастает его удельный объем 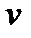 ), то обязательно совершается работа, связанная с увеличением
), то обязательно совершается работа, связанная с увеличением 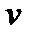 ; дифференциал этой работы всегда равен
; дифференциал этой работы всегда равен 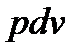 .
.
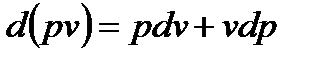
Для любого потока
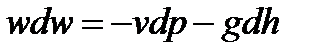
Если 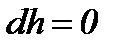 , то
, то
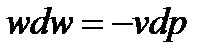
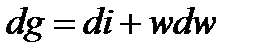
Для адиабатного потока 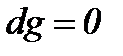

Интегрируя уравнение (8-3) между двумя точками потока, получаем:
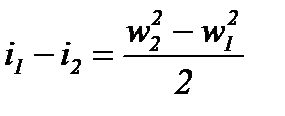 (8-8)
(8-8)
откуда
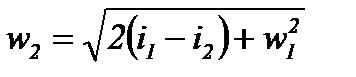 (8-9)
(8-9)
К решению задачи об определении скорости потока в точке 2 по известным значениям термических параметров состояния и скорости в точке 1 и давления в точке 2 можно подойти и другим путем.
Напомним, что, как показано в гл. 2, для течения без трения при 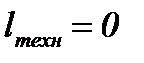 и
и 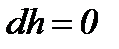 справедливо уравнение (2-73)
справедливо уравнение (2-73)
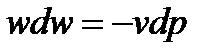 .
.
Интегрируя это соотношение, имеем:
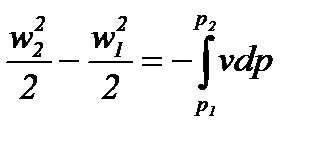 (8-10)
(8-10)
или, что то же самое,
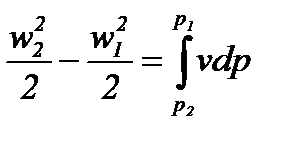 (8-10а)
(8-10а)
Отсюда
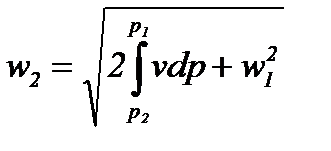 (8-11)
(8-11)
Скорость звука
Как известно, скоростью звука называется скорость распространения в среде малых возмущений (малыми называются такие возмущения среды, в которых местное изменение давления среды в точке возмущения, т.е. амплитуда давления, пренебрежимо мало по сравнению с общим давлением).
Отсюда следует, что скорость распространения малых возмущений (скорость звука в среде) определяется соотношением
 (8-21)
(8-21)
Для расчета скорости звука в газах это уравнение впервые было применено в 1687 г. Ньютоном. Для того чтобы воспользоваться уравнением (8-21), нужно знать, как происходит процесс распространения звуковых волн, т.е. для таких условий следует вычислять производную 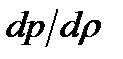 .
.
Ньютон считал, что процесс распространения звука в газе происходит в изотермических условиях. Воспользовавшись уравнением Бойля – Мариотта для изотермического процесса в идеальном газе
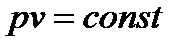 ,
,
откуда следует, что
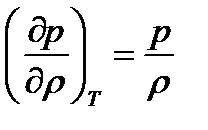 , (8-22)
, (8-22)
Ньютон вычислил скорость звука в воздухе при атмосферном давлении и комнатной температуре (при этих параметрах воздух с хорошим приближением можно рассматривать как идеальный газ). Однако в прямых измерениях скорости звука в воздухе было получено значение 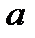 , примерно на 20% превосходящее величину, найденную Ньютоном.
, примерно на 20% превосходящее величину, найденную Ньютоном.
Причина этих расхождений была установлена Лапласом, который отметил, что поскольку звуковые колебания в среде распространяются очень быстро, то сколько-нибудь заметного теплообмена между зонами разрежения и сжатия звуковой волны и окружающей средой не успевает произойти, поэтому колебания среды при распространении звуковой волны можно считать адиабатными и изоэнтропными. Поэтому производную, стоящую в уравнении (8-21), следует брать при условии 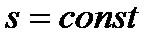 , т.е.
, т.е.
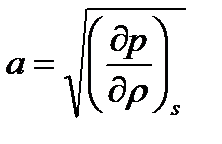 (8-21а)
(8-21а)
Уравнение (8-21а) носит название уравнения Лапласа. Уравнение Лапласа позволяет по известной величине 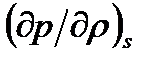 вычислить скорость распространения звука в среде.
вычислить скорость распространения звука в среде.
Запишем уравнение Лапласа (8-21а) в следующем виде:
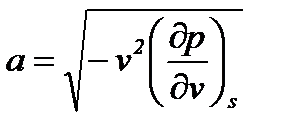 (8-23)
(8-23)
где 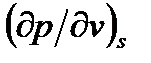 - величина, обратная адиабатной сжимаемости вещества.
- величина, обратная адиабатной сжимаемости вещества.
Поскольку величины 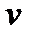 и
и 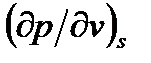 являются функциями состояния, величина скорости звука
являются функциями состояния, величина скорости звука 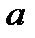 , определяемая уравнением Лапласа, также является термодинамической функцией состояния.
, определяемая уравнением Лапласа, также является термодинамической функцией состояния.
Напомним, что ранее (§ 7-4) показатель изоэнтропы был определен нами следующим образом:
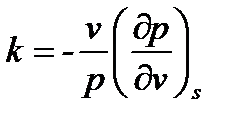
Из (8-23) и (7-44) очевидно, что
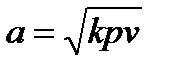 (8-24)
(8-24)
Уравнение (8-24) позволяет определить величину 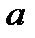 по известным значениям давления
по известным значениям давления 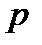 , удельного объема среды
, удельного объема среды 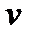 и показателя изоэнтропы (адиабаты)
и показателя изоэнтропы (адиабаты) 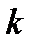 .
.
С учетом уравнения Клапейрона (1-23)
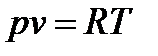
получаем для случая идеального газа:
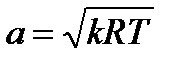 (8-25)
(8-25)
Дата добавления: 2016-06-05; просмотров: 1648;











