Основы теории манипуляционных механизмов

Исполнительным устройством робота является манипулятор, снабженный на свободном конце захватом. Звенья манипулятора соединяются друг с другом с помощью кинематических пар-вращательных и поступательных. Каждая кинематическая пара получает движение от управляемого привода. Все приводы объединены единой системой управления робота для координации движения всех звеньев манипулятора в соответствии с программой выполнения технологического процесса.

Для полного осуществления пространственного движения необходимо иметь в манипуляторе шесть степеней подвижности (рис.2.3.1).

Кинематические пары и звенья объединяются в кинематическую цепь. Кинематические цепи разделяются на замкнутые и разомкнутые.

Замкнутой называют кинематическую цепь, каждое звено которой входит по меньшей мере в две кинематические пары.

Число степеней свободы кинематической цепи будет определяться соотношением

,

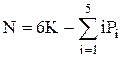где К - число звеньев кинематической цепи;

6К- число степеней свободы несоединенных звеньев в кинематические пары;

Р_i - число кинематических пар в цепи i -го класса.

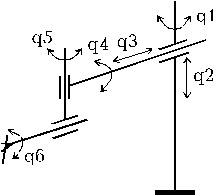
Рис.2.3.1. Обобщенные координаты положения
звеньев манипулятора

Обычно роботы снабжены манипуляторами, представляющими незамкнутую кинематическую цепь. Отсюда специфика теории манипуляторов состоит в том, что к ним предъявляются высокие требования по точности и быстродействию при самых различных условиях движения объекта:

- отработка заданных положений в пространстве координат;

- отработка заданных скоростей в этих координатах;

- отработка ускорений и усилий.

Все это требует для анализа промышленных роботов использования средств и методов механики, теории механизмов, теории автоматического регулирования, теории упругости и колебаний, теории привода.

Положение кинематической незамкнутой цепи в пространстве определяется с помощью обобщенных координат q_i (i=1,2,...n) (рис.2.3.1), которые характеризуют относительные перемещения звеньев как поступательные, так и вращательные.

Координаты q₁, q₂, q₃ характеризуют переносные перемещения, а q₄, q₅, q₆ - ориентирующие.

На рис.2.3.2. изображены расчетные кинематические модели только для переносных перемещений в цилиндрической (а), сферической (б) и угловой (в) системах координат. В первом случае имеем q₁=Z₀, q₂=j, q₃=r, во втором q₁= j, q₂= j₂, q₃=r, в третьем - q₁= j₁, q₂= j₂, q₃=j₃.

Рис.2.3.2. Кинематические схемы систем координат
манипуляторов: а - цилиндрическая; б - сферическая;
в - угловая

Координаты концевой точки манипулятора Р в рабочем пространстве определяются в случае цилиндрической системы:

X_p=rCosj; Y_p=rSinj; Z_p=Z₀. (2.3.1)

Для сферической системы точка Р будет описана

X_p=rCosj₁Cosj₂; Y_p=rSinjCosj₂; Z_p=l+rSinj₂. (2.3.2)

В угловой системе получим

X_p=l₂Cosj₁Cosj₂+l₃Cosj₁Cos(j₂+j₁);

Y_p=l₂Sinj₂Cosj₂+l₃Sinj₁Cos(j₂+j₁);

Z_p=l₁+l₂Sinj₂+l₃Sin(j₂+j₁). (2.3.3)

В теории манипуляторов решается прямая задача - определение абсолютного положения звеньев относительно неподвижной системы координат (2.3.1)...(2.3.3) - при известных обобщенных координатах q_i.

Обратная задача заключается в определении обобщенных координат q_i относительного положения звеньев друг относительно друга.

Решение прямой и обратной задач положения осуществляется различными методами: аналитическим, геометрическим, векторным, матричным и векторно-матричным.

В большинстве случаев используют векторно-матричные методы решения, обладающие рядом преимуществ:

- простотой и наглядностью записи формул;

- удобством применения для численных расчетов на ЭВМ;

- единообразием использования для анализа как разомкнутых, так и замкнутых кинематических цепей.

Преобразуем запись определения координат (2.3.1)...(2.3.3) в векторно-матричную форму:

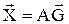, (2.3.4)

где =(X_p, Y_p, Z_p) - вектор точки Р в неподвижных координатах;

=(r, j, z) - вектор точки Р в относительных координатах (обобщенных координатах);

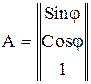- матрица преобразования координат из цилиндрической

в декартову систему (2.3.5);

- матрица преобразования координат из сферической в декартову (2.3.6).

Тогда обратная задача положения манипулятора может быть записана в очень удобном виде:

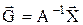, ( 2.3.7)

где A^-1 - матрица, обратная матрице А .

В аналогичной постановке решаются прямые и обратные задачи об определении скоростей и ускорений рабочего органа в точке Р и звеньев манипулятора.

На основе кинематического анализа звеньев манипулятора проводится динамический анализ с определением сил инерции и моментов сил в звеньях и в кинематических парах.