Геометрический метод.

Применяют для исследования точности только механизмов. Все соотношения между погрешностью ведомого звена и первичными погрешностями звеньев находятся на основании геометрических построений. Суть метода: механизм строится в двух наложенных друг на друга положениях при одном и том же положении ведущего звена, но один раз при отсутствии первичной погрешности, а другой раз – при её наличии. Эти построения механизма выполняются при резко увеличенных значениях первичных погрешностей.

При выводе формул, связывающих погрешность механизма с первичными погрешностями, вводят ряд упрощений, сущность которых заключается в исключении погрешностей второго порядка малости (линеаризация погрешности выходного сигнала).

Это выражается в следующем: в независимом рассмотрении каждой первичной погрешности и в использовании ряда приближений, из которых наиболее часто используются следующие:

1) Синус малого угла принимают равным малому углу: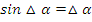

2)

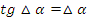
3)

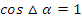
4) Тангенс, синус и косинус суммы значительного или малого угла равны соответственно тангенсу, синусу и косинусу значительного угла.

Малый угол – это угол, вызванный первичной погрешностью при значении катета и гипотенузы не менее, чем на 4, а в крайнем случае – на 3 порядка больше, чем порядок погрешности.

Достоинства метода:

1.Не требует градуировочной характеристики.

2.Нет необходимости в преобразованном механизме.

3.Для сложных механизмов достаточно трудно найти передаточное отношение между первичной погрешностью и погрешностью положения ведомого звена. Этот метод избавляет от этого.

Недостатки метода:

1.Неуниверсален.

2.Невысокая точность.