Многоканальные СМО с очередью.

Будем рассматривать системы (Р/Е/s):(d/d+s/¥) в предположении, что время обслуживания не зависит от входного потока и все линии работают независимо. Будем говорить, что в системе установилсястационарный режим работы, если среднее число поступающих требований меньше среднего числа требований, обслуженных на всех линиях системы, т.е. l<m*s(или j=y/s< 1). Анализ систем такого рода показывает, что

,

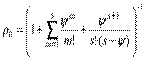а 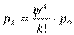, для k=1,2,…

Характеристики.

Как и одноканальные СМО с ожиданием, многоканальные СМО характеризуются некоторыми характеристиками. Нас интересуют средние значения этих величин.

j – количество занятых линий обслуживания, .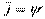

r – число свободных линий, .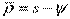

v – длина очереди, .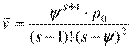

w – время ожидания начала обслуживания, .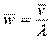

P(w>0) – вероятность ожидания начала обслуживания, .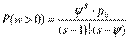

Последняя характеристика позволяет решать задачу об определении оптимального числа каналов обслуживания с таким расчетом, чтобы вероятность ожидания начала обслуживания была меньше заданного числа. Для этого достаточно просчитать вероятность ожидания последовательно при s =1, s =2, s=3 и т.д.

ПРИМЕР.

СМО – станция скорой помощи небольшого микрорайона. l=3 вызова в час, а m = 4 вызова в час для одной бригады. Сколько бригад необходимо иметь на станции, чтобы вероятность ожидания выезда была меньше 0.01?

Решение. Коэффициент загрузки системы y=0.75. Предположим, что в наличие имеется две бригады. Найдем вероятность ожидания начала обслуживания

при s=2. , .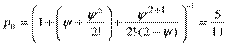

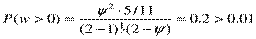Предположим наличие трех бригад, т.е. s =3. По формулам получим, что р0=8/17, Р(w>0)=0.04>0.01.

Предположим, что на станции четыре бригады, т.е. s =4. Тогда получим, что р0=416/881, Р(w>0)=0.0077<0.01. Следовательно, на станции должно быть четыре бригады.