Кручение. Построение эпюр
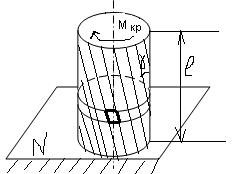
Рассмотрим брус круглого поперченного сечения, один конец которого закреплён на неподвижной плоскости N, а к другому приложен крутящей момент. Такой брус будет испытывать деформацию кручению. Ось бруса при кручении остаётся прямой и называется осью кручения. Эксперименты показывают, что все образующие поворачиваются на один и тот же угол γ, т.е. превращаются в винтовые линии с большим шагом. Поперечное сечение поворачивается одно относительно другого вокруг оси кручения на некоторый угол, называемый углом закручивания. Прямоугольники сетки, нанесённые на поверхность круглого бруса, превращаются в параллелограммы или ромбы. Угол поворота кольцевого сечения бруса относительно неподвижного конца называется полным углом закручивания
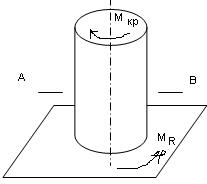
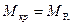
Для того чтобы определить крутящий момент, воспользуемся методом сечения. Рассечём сечение в произвольной точке. Одну часть отбросим, к оставшейся приложим внутренний крутящий момент, заменяющий момент отброшенной части.
Для определения знака крутящего момента, независимо от того, к какой из оставшейся части он приложен, принято следующее правило знаков. Внутренний момент кручения считается положительным, если мы видим его направление по ходу движения часовой стрелки со стороны направленного сечения, и отрицательным – наоборот.
Построение эпюры крутящего момента:
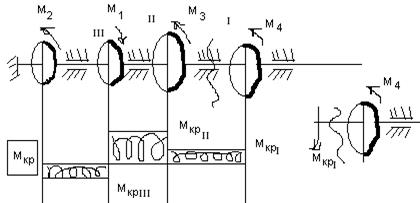
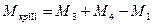
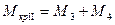
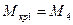
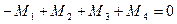
Дата добавления: 2021-12-14; просмотров: 408;











