Числовые характеристики дискретных случайных величин

Характеристикой среднего значения случайной величины слу­жит математическое ожидание.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:

Если дискретная случайная величина принимает счетное множество возможных значений, то

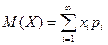
причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Математическое ожидание обладает следующими свойствами.

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:

М(С) = С.

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:

М(СХ) = СМ(Х).

Свойство 3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:

М (Х₁Х₂ ... Х_п) = М (Х_г) ∙М (Х₂) ... М (Х_п).

Свойство 4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:

M(X 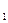+ X_t+ ...+ Х_п) = М(Х₁)+М(Х_г)+ ...+М(Х_п).

Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании:

М(Х) = пр.

Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.

Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от ее матема­тического ожидания:

D(X) = M[X~ M(X)]².

Дисперсию удобно вычислять по формуле

D(X)=M(X²) — [M(X)]².

Дисперсия обладает следующими свойствами.

Свойство 1. Дисперсия постоянной равна нулю:

D(C)=0.

Свойство 2. Постоянный множитель можно выносить за знак диcnepcuи, предварительно возведя его в квадрат:

D(CX) = C²D(X).

Свойство 3. Дисперсия суммы независимых случайных вели­чин равна сумме дисперсий слагаемых:

D(X₁ + X₂+...+X_n) = D(X_l) + D(X_t)+ …+D{X_H).

Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события! в одном испытании:

D(X) = npq.

Средним квадратическим отклонением случайной величины на­зывают квадратный корень из дисперсии:

).

63.Найти математическое ожидание дискретной слу­чайной величины X, заданной законом распределения:

а) X – 4 6 10 б) X 0,21 0,54 0,61

р 0,2 0,3 0,5 ; р 0,1 0,5 0,4 '

Решение, а) Математическое ожидание равно сумме произ­ведений всех возможных значений X на их вероятности:

М (Х) = - 4∙0,2+6∙0,3 4+10∙0,5 = 6.

64.Найти математическое ожидание случайной вели­чины Z, если известны математические ожидания X и Y:

a) Z = X + 2Y, М(Х) = 5, M{Y) = 3; б) Z = 3X+4Y, М(Х) = 2, М(Y) = 6.

Решение, а) Используя свойства математического ожидания (математическое ожидание суммы равно сумме математических ожи­даний слагаемых; постоянный множитель можно вынести за знак математического ожидания), получим

М (Z) = М (X + 2Y) = М (X) + М (2Y) = М{Х) + 2М (Y) = = 5+2∙3 = 11.

65.Используя свойства метематического ожидания, доказать, что: а) М (X – Y) = М (X) – М (К); б) матема­тическое ожидание отклонения X – М (X) равно нулю.

66.Дискретная случайная величина X принимает три возможных значения: x₁ = 4 с вероятностью р_х = 0,5; х₂ = 6 с вероятностью р₂ = 0,3 и х₃ с вероятностью p₃.Найти х₃ и р₃, зная, что М(Х) = 8.

67.Дан перечень возможных значений дискретной случайной величины Х: 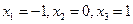, а также известны математические ожидания этой величины и е квадрата: М(Х) = 0,1, 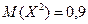. Найти вероятности 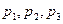, соответствующие возможным значениям .

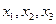Решение. Пользуясь тем, что сумма вероятностей всех воз­можных значений X равна единице, а также принимая во внима­ние, что М (X)=0,l , 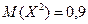, составим следующую систему трех линейных уравнений относительно неизвестных вероятностей:

,

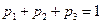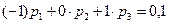
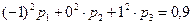
Решив эту систему, найдем искомые вероятности: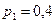

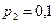
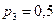
68. Случайные величины X и Y независимы. Найти дисперсию случайной величины Z = 2X + 3K, если из­вестно, что D(X) = 4, D(Y) = 5.

69. Найти дисперсию и среднее квадратическое от­клонение дискретной случайной величины X, заданной законом распределения:

X – 5 2 3 4

р 0,4 0,3 0,1 0,2

Решение. Дисперсию можно вычислить исходя из ее опреде­ления, однако мы воспользуемся формулой

,

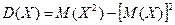которая быстрее ведет к цели.

Найдем математическое ожидание X:

М(Х) = —5.0,4 + 2-0,3 + 3.0,1-f 4.0,2 = — 0,3.

Напишем закон распределения X²:

Х² 25 4 9 16

р 0,4 0,3 0,1 0,2

Найдем математическое ожидание X²:

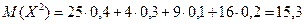
.Найдем искомую дисперсию:

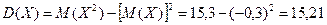
Найдем искомое среднее квадратическое отклонение:

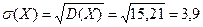
70. Найти дисперсию и среднее квадратическое от­клонение дискретной случайной величины X, заданной законом распределения:

а) X 4,3 5,1 10,6 б) X 131 140 160 180

р 0,2 0,3 0,5' р 0,05 0,10 0,25 0,60

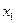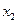71. Дискретная случайная величина X имеет только два возможных значения и , причем равновероят­ных. Доказать, что дисперсия величины X равна квад­рату пол у разности возможных значений:

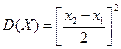
Решение. Найдем математическое ожидание X, учитывая, что вероятности возможных значени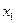й и 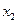, равны между собой и, следовательно, каждая из них равна ¹/₂ :

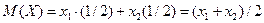
Найдем математическое ожидание X²:

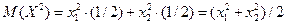
Найдем дисперсию X:

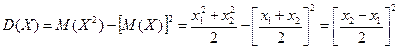
72.Найти дисперсию дискретной случайной вели­чины X – числа появлений события А в пяти независи­мых испытаниях, если вероятность появления событий А в каждом испытании равна 0,2.

Решение. Дисперсия числа появлений события в независимых испытаниях (с одинаковой вероятностью появления события в каж­дом испытании) равна произведению числа испытаний на вероятнос­ти появления и непоявления события:

D(X) = npq.

По условию, n = 5; р = 0,2; q = 1–0,2 = 0,8.

Искомая дисперсия

D (X) = npq = 5∙0,2∙0,8 = 0,8.