Множественная линейная регрессия
Задание 2.11.1.
Построить линейную модель по следующим данным, собранным о сотрудниках фирмы.
Таблица 2.11.1
| № | Образование, лет | Текущая з/п, $ | Начальная з/п, $ | Проработанное время, мес. | Предшествующий опыт, мес. |
| 57,000 | 27,000 | ||||
| 40,200 | 18,750 | ||||
| 60,625 | 22,500 | ||||
| 39,900 | 15,750 | ||||
| 26,250 | 10,950 | ||||
| 22,200 | 15,000 | ||||
| 42,300 | 26,250 | ||||
| 30,750 | 15,000 | ||||
| 26,700 | 12,900 | ||||
| 20,850 | 12,000 | ||||
| 35,250 | 15,000 | ||||
| 26,700 | 15,000 | ||||
| 26,550 | 13,050 | ||||
| 66,750 | 52,500 | ||||
| 66,875 | 31,980 | ||||
| 30,000 | 15,750 | ||||
| 83,750 | 21,750 | ||||
| 24,450 | 10,950 | ||||
| 31,950 | 15,750 | ||||
| 33,900 | 15,750 |
Выполнение.
При построении линейной модели в качестве исследуемой переменной (зависимой) рассмотрим размер текущей з/п.
Выберем в меню Analyze (Анализ) Regression (Регрессия) Linear (Линейная). Появится диалоговое окно (см. рис. 2.11.1).
Рис. 2.11.1. Диалоговое окно «Линейная регрессия»
Поместим переменную тек_з_п в поле для зависимых переменных, а остальные переменные в поле для независимых переменных.
Для множественного анализа с несколькими независимыми переменными не рекомендуется оставлять метод включения всех переменных, установленный по умолчанию.
Этот метод соответствует одновременной обработке всех независимых переменных, выбранных для анализа, и поэтому он может рекомендоваться для использования только в случае простого анализа с одной независимой переменной.
Для множественного анализа следует выбрать один из пошаговых методов. При прямом методе независимые переменные, которые имеют наибольшие коэффициенты частной корреляции с зависимой переменной, пошагово увязываются в регрессионном уравнении.
При обратном методе начинают с результата, содержащего все независимые переменные, и затем исключают независимые переменные с наименьшими частными корреляционными коэффициентами, пока соответствующий регрессионный коэффициент не оказывается незначимым (в данном случае уровень значимости равен 0,1).
Наиболее распространенным является пошаговый метод, который устроен так же, как и прямой метод, однако после каждого шага переменные, используемые в данный момент, исследуются по обратному методу.
При пошаговом методе могут задаваться блоки независимых переменных; в этом случае заданные блоки на одном шаге обрабатываются совместно.
Выберем пошаговый метод, но воздержимся от блочной формы ввода данных, не задавая больше ни каких дополнительных расчётов, и начнем вычисление нажатием ОК.
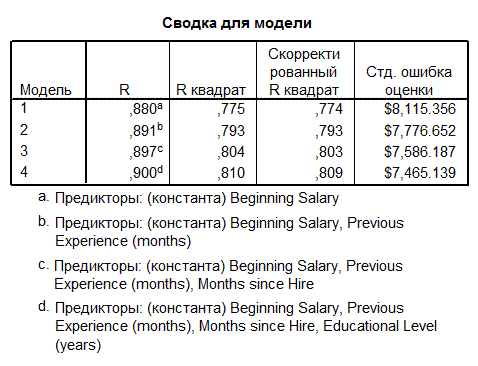
Рис. 2.11.2. Результаты анализа «Сводка для модели»
Из таблицы «Сводка для модели» следует, что вовлечение переменных в расчет производилось за четыре шага, то есть переменные образование, начальная з/п, проработанное время, предшествующий опыт работников поочерёдно внедрялись в уравнение регрессии.
Для каждого шага происходит вывод коэффициентов множественной регрессии, меры определённости, смещенной меры определённости и стандартной ошибки.
К указанным результатам пошагово присоединяются результаты расчёта дисперсии, которые здесь не приводятся.
Также, пошаговым образом, производится вывод соответствующих коэффициентов регрессии и значимость их отличия от нуля (рис. 2.11.3).
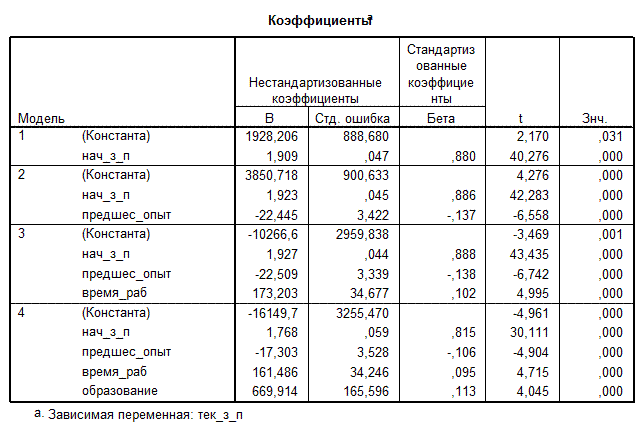
Рис. 2.11.3. Коэффициенты линейной модели
Уравнение регрессии для прогнозирования значения тек_з_п выглядит следующим образом:
тек_з_п = 669,914×образование + 161,486×время_раб – 17,303×предшес_опыт + 1,768×нач_з_п
При помощи соответствующих опций можно организовать вывод большого числа дополнительных статистических характеристик и графиков.
Можно также создать много дополнительных переменных и добавить их в исходный файл данных.
Пример 2.11.2. Имеются 12 наблюдений за тремя показателями:
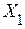
| ||||||||||||
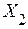
| ||||||||||||
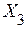
| ||||||||||||
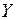
|
Используя пакет для обработки статистических данных получить уравнение множественной линейной регрессии и проанализировать качество полученной модели.
Решение.Построим уравнение регрессии в виде
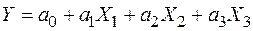 .
.
Создадим в пакете SPSS 13 файл с данными:
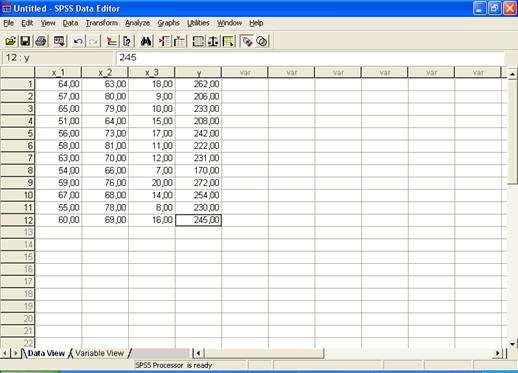
Выберем в меню пункты (опции) Analyze... (Анализ) Regression...(Регрессия) Linear... (Линейная). Появится диалоговое окно Linear Regression (Линейная регрессия) (рис.5.4).
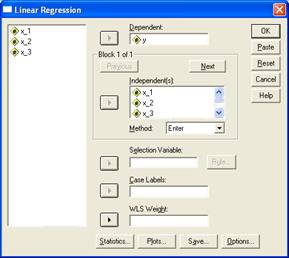
Перенесем переменную Y в поле для зависимых переменных и присвоим переменным x_1, x_2, x_3 статус независимых переменных.
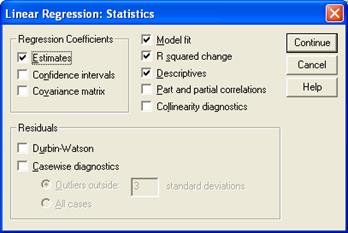
После нажатия кнопки «Statistics…» в появившемся окне установим флажки напротив опций «R squared change» и «Descriptives», далее нажимаем клавишу «Continue» (рис.5.5).
Расчет параметров модели начинается нажатием клавиши ОК.
| 
|
| Рис.2.11.4. Вид диалогового окна «Линейная регрессия» | Рис.2.11.5. Вид диалогового окна «Статистика линейной регрессии» |
Вывод основных результатов выглядит следующим образом:
Descriptive Statistics
| Mean | Std.Deviation | N | |
| y x_1 x_2 x_3 | 231.2500 59.0833 72.2500 13.0833 | 27.71322 4.87029 6.44029 4.20948 |
Variables Entered/Removedb
| Model | Variables Entered | Variables Removed | Method |
| x_3,a x_1, x_2 | Enter |
a. All requested entered
b. Dependent Variable: y
Correlations
| y | x_1 | x_2 | x_3 | |
| Pearson Correlation y x_1 x_2 x_3 | 1.000 .595 .019 .770 | .595 1.000 –.012 .204 | .019 –.012 1.000 –.353 | .770 .204 –.353 1.000 |
| Sig. (1–tailed) y x_1 x_2 x_3 | . 0.21 .476 .002 | .021 . .485 .263 | .476 .485 . .130 | .002 .263 . |
| N y x_1 x_2 x_3 |
Model Summarry
| Model | R | R Square | Adjusted R Square | Std.Error of the Estimate | Change Statistics | ||||
| R Square Change | F Change | df1 | df2 | Sig.F Change | |||||
| .934a | .873 | .825 | 11.58090 | .873 | 18.331 | .001 |
a. Predictors: (Constant), x_3, x_1, x_2
ANOVAb
| Model | Sum of Squares | df | Mean Square | F | Sig. |
| 1 Regression Residual Total | 7375.313 1072.937 8448.250 | 2458.438 134.117 | 18.331 | .001a |
a. Predictors: (Constant), x_3, x_1, x_2
b. Depended Variable: y
Coefficientsa
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | |
| B | Std.Error | Beta | |||
| 1 (Constant) x_1 x_2 x_3 | –78.166 2.496 1.303 5.183 | 60.771 .734 .581 .907 | .439 .303 .787 | –1.286 3.402 2.243 5.712 | .234 .009 .055 .000 |
Основные числовые характеристики исследуемых показателей будут следующие: 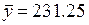 ;
; 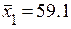 ;
; 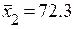 ;
; 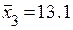 ;
;
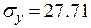 ;
; 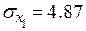 ;
; 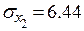 ;
; 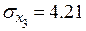 .
.
Параметры модели регрессии представлены в таблице «Coefficients».
Таким образом уравнение множественной регрессии имеет вид:
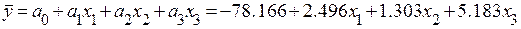 .
.
Для сравнения влияния каждой независимой переменной вычислим стандартизированные коэффициенты регрессии
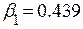 ;
; 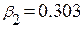 ;
; 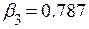 .
.
Увеличение показателя 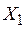 только на одно значение
только на одно значение 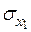 увеличивает в среднем показатель
увеличивает в среднем показатель 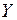 на
на 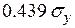 .
.
Аналогично, увеличение 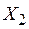 на значение
на значение 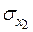 увеличивает
увеличивает 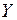 на
на 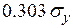 . Увеличение
. Увеличение 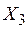 на
на 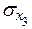 увеличивает
увеличивает 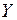 на
на 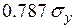 .
.
Коэффициенты эластичности будут равны
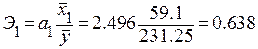 ;
;
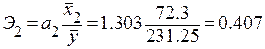 ;
;
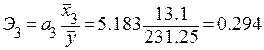 .
.
Увеличение переменных 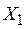 ,
, 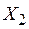 и
и 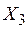 на 1% от своих средних значений приводит в среднем к увеличению
на 1% от своих средних значений приводит в среднем к увеличению 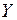 соответственно на 0.638 %, 0.407 % и 0.294 %.
соответственно на 0.638 %, 0.407 % и 0.294 %.
Проверим значимость модели множественной регрессии по 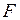 –критерию. Выдвигаем гипотезу
–критерию. Выдвигаем гипотезу 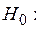 уравнение незначимо.
уравнение незначимо.
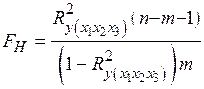 ,
,
где 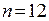 − количество наблюдений,
− количество наблюдений, 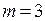 − количество показателей.
− количество показателей.
Коэффициент детерминации модели
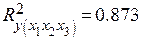 .
.
Наблюдаемое значение критерия
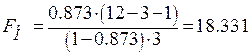 .
.
Отметим, что вычисления в пакете SPSS 13 дают то же значение
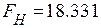 .
.
По таблице 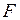 –распределения найдем критическую точку
–распределения найдем критическую точку
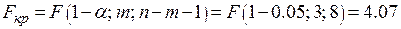 .
.
Так как 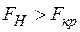 , то есть все основания отвергнуть гипотезу
, то есть все основания отвергнуть гипотезу 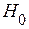 , то есть модель регрессии значима при уровне значимости
, то есть модель регрессии значима при уровне значимости 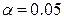 .
.
Проверим на значимость коэффициенты 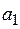 ,
, 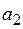 и
и 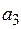 с помощью
с помощью 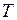 –критерия Стьюдента.
–критерия Стьюдента.
Имеем
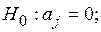
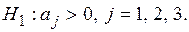
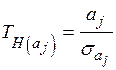 ,
,
где 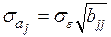 ,
, 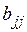 − диагональные элемента матрицы
− диагональные элемента матрицы 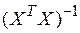 .
.
Вычислим дисперсию остатков модели по соотношению
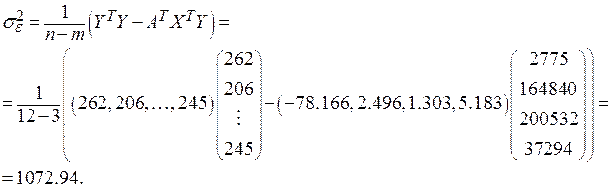
Средняя ошибка (точность) модели
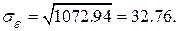
Тогда
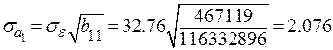 ;
; 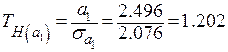 ;
;
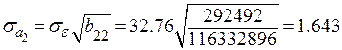 ;
; 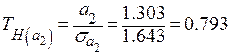 ;
;
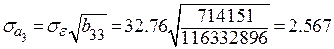 ;
; 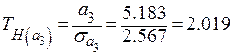 .
.
По таблице квантилей 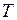 –распределения Стьюдента найдем критическую точку.
–распределения Стьюдента найдем критическую точку.
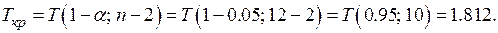
Так как 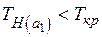 и
и 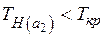 , то нет оснований отвергать гипотезу
, то нет оснований отвергать гипотезу 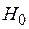 , то есть коэффициенты
, то есть коэффициенты 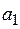 и
и 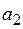 незначимы.
незначимы.
Так как 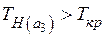 , то гипотезу
, то гипотезу 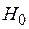 отвергаем, то есть коэффициент
отвергаем, то есть коэффициент 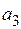 значим.
значим.
Дата добавления: 2022-05-27; просмотров: 164;











