Дисперсионный анализ
Задание 2.5.
Исследовать влияние работы трёх филиалов предприятия на получение им месячной прибыли. Данные приведены в таблице 2.5.1
Таблица 2.5.1
| Филиал предприятия | Прибыль |
| 35,8; 43,5; 30,7; 34,0; 33,2; 31,7; 31,6; 34,0; 33,2 | |
| 31,4; 44,5; 43,0; 48,7; 41,6; 43,8; 42,2; 45,0; 41,9 | |
| 32,8; 40,3; 40,5; 45,3; 41,4; 41,3; 40,8; 39,2 |
Выполнение.
В рамках однофакторного дисперсионного анализа предусмотрена процедура One–Way ANOVA, которая заключается в анализе влияния одного качественного фактора на количественную переменную.
Требуется указать список количественных переменных и фактор, от которого они зависят.
Имеем задачу однофакторного дисперсионного анализа с наблюдениями на трех уровнях.
Качественным показателем, влияющим на количественную переменную (прибыль по филиалам), является номер филиала предприятия.
Выполним следующие действия.
· Создадим и загрузим файл данных (рис. 2.5.1).
Рис. 2.5.1. Фрагмент файла данных
· Выберем в меню команды Analyze (Анализ) Compare Means (Сравнение средних) One–Way ANOVA (Однофакторный дисперсионный анализ). Появится диалоговое окно односторонний ANOVA (рис. 2.5.2).
· Перенесем переменную Прибыль в список зависимых переменных, a переменную Филиал – в поле «Фактор».
· Зададим вывод описательной статистики, для этого щелкнем на кнопке «Параметры» и в открывшемся окне (рис. 2.5.3) установим флажок «Описательный».
Рис. 2.5.2. Диалоговое окно «Однофакторный дисперсионный анализ»
Рис. 2.5.3. Диалоговое окно
«Однофакторный дисперсионный анализ: Опции»
Запустим тест, щелкнув на ОК.
Получим следующие результаты.
| N | Mean | Std. deviation | Std. Error | 95% Confidence interval for Mean | Minimum | Maximum | ||
| Lower Bound | Upper Bound | |||||||
| 1,00 | 34,1889 | 3,81426 | 1,27142 | 31,2570 | 37,1208 | 30,70 | 43,50 | |
| 2,00 | 42,4556 | 4,67817 | 1,55939 | 38,8596 | 46,0515 | 31,40 | 48,70 | |
| 3,00 | 40,2000 | 3,48220 | 1,23114 | 37,2888 | 43,1112 | 32,80 | 45,30 | |
| Total | 38,9000 | 5,30434 | 1,04027 | 36,7575 | 41,0425 | 30,70 | 48,70 |
ANOVA
Прибыль
| Sum of Squares | df | Mean Square | F | Sig | |
| Between Groups | 327,049 | 163,524 | 9,993 | ,001 | |
| Within Groups | 376,351 | 16,363 | |||
| Total | 703,400 |
Рис. 2.5.4. Результат выполнения процедуры
Таким образом, имеем следующие характеристики:
· 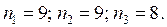
· Средние значения переменной на i–м уровне  .
.  .
.
· Среднее значение переменной по всем значениям 
· Сумму квадратов отклонений всех наблюдений от общего среднего 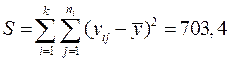 .
.
· Сумму квадратов отклонений средних групповых значений 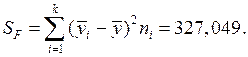
· Остаточную сумму квадратов отклонений
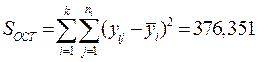 .
.
Отметим справедливость соотношения 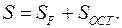
Нулевая гипотеза принимается при. 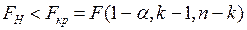
Проверим гипотезу для уровня 0,05: 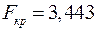 ;
; 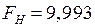 .
.
Имеем, что 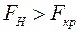 , нулевую гипотезу отвергаем и делаем вывод, что работа в каждом из филиалов влияет на месячную прибыль предприятия.
, нулевую гипотезу отвергаем и делаем вывод, что работа в каждом из филиалов влияет на месячную прибыль предприятия.
Наглядным представлением результатов являются графики средних значений и их доверительных интервалов (простая диаграмма величины ошибки) (рис.2.5.7).
Построим подобный график, для этого выполним следующие действия:
· Выберем команду «Визуализация/Колонка ошибок» и в открывшемся окне (рис. 2.5.5) выберем вариант «Простой» и нажмем на кнопку «Определ.».
· В появившемся диалоговом окне (рис. 2.5.6) заполним следующие поля. Переменная в рассматриваемом случае это переменная Прибыль. Ось категорий – поле факторной переменной (переменной, содержащей категории), для данного примера это переменная Филиал. Изобразить панели – что следует отразить на графике: доверительный интервал для математического ожидания, стандартную ошибку математического ожидания или среднеквадратичное отклонение. Нас интересует доверительный интервал для математического ожидания. Уровень – пределы доверительного интервала (по умолчанию стоит значение 95%).
Рис. 2.5.5. Диалоговое окно «Колонка Ошибок»
Рис. 2.5.6. Диалоговое окно
Запустим выполнение, щелкнув на ОК.
Получим следующий график (рис. 2.5.7).
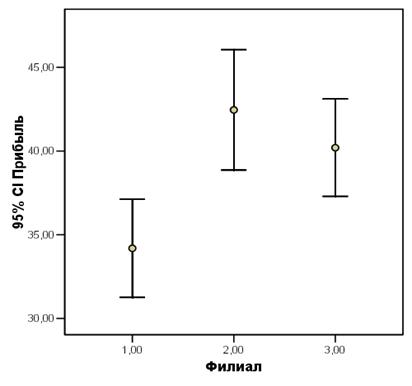
Рис. 2.5.7. Результат выполнения процедуры
«Визуализация/Колонка ошибок»
Ряды динамики
Задание 2.6.
Необходимо выявить сезонную компоненту (расход воды жителями какого–то города).
Выполнение.
Для этого необходимо ввести данные, как показано на рис. 2.6.1.
Затем выбираем:
«Анализ – Временные ряды – Сезонное разложение» (рис.2.6.2).
Далее выбираем модель мультипликативную (умножение), перетаскиваем нашу исследуемую величину (рис.2.6.3).
Как видно, здесь уже автоматически подсчитана периодичность.
Нажимаем OK.
Получаем вывод (рис.2.6.4).
Если вернуться в редактор данных, то увидим, что к исходным данным добавились еще переменные: ERR_1, SAS_1, SAF_1, STC_1 (рис. 2.6.5).
Здесь:
первая переменная – это отклонение объема потребления от средней за год,
вторая – сезонная характеристика ряда,
третья – сезонный фактор, четвертая – тренд.
Теперь сделаем все тоже, но только с аддитивной моделью.
Для этого в диалоговом окне (рис.2.6.6) отметим положительная модель.
В результате получим следующий вывод рис.2.6.7.
Если вернуться в редактор данных, то снова можно убедиться в появлении новых переменных: ERR_2, SAS_2, SAF_2, STC_2, имеющих аналогичный смысл что и ERR_1, SAS_1, SAF_1, STC_1.
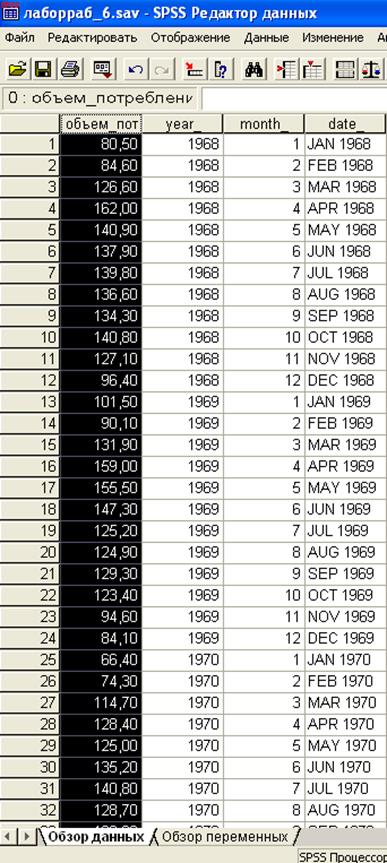
Рис. 2.6.1. Редактор данных (выделенный столбец – yt)
Рис. 2.6.2. Выбор необходимого пункта меню
Рис. 2.6.3 Диалоговое окно «Сезонное Разложение»
Seasonal Decomposition
Model Description
| Model Name | MOD_4 | |
| Model Type | Multiplicative | |
| Series Name | объем_потребления | |
| Length of Seasonal Period | ||
| Computing Method of Moving Averages | Span equal to the periodicity and all points weighted equally | |
Applying the model specifications from MOD_4
Seasonal Factors
Series Name: объем_потребления
| PPeriod | Seasonal Factor (%) |
| 65,6 | |
| 69,4 | |
| 101,1 | |
| 114,6 | |
| 120,4 | |
| 119,4 | |
| 112,5 | |
| 113,5 | |
| 106,3 | |
| 110,2 | |
| 92,2 | |
| 74,9 |
Рис.2.6.4. Результат выполнения «Сезонного Разложения»
(мультипликативная модель)
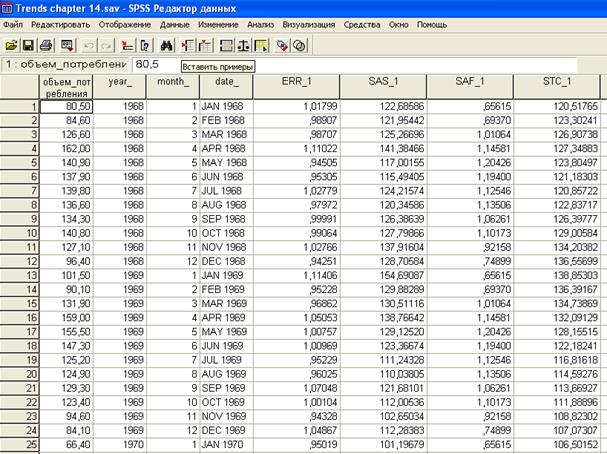
Рис. 2.6.5. В редакторе данных появились новые переменные
Рис. 2.6.6. Диалоговое окно «Сезонное Разложение»
Seasonal Decomposition
Model Description
| Model Name | MOD_5 | |
| Model Type | Additive | |
| Series Name | объем_потребления | |
| Length of Seasonal Period | ||
| Computing Method of Moving Averages | Span equal to the periodicity and all points weighted equally | |
Applying the model specifications from MOD_5
Seasonal Factors
Series Name: объем_потребления
| PPeriod | Seasonal Factor |
| –47,45827 | |
| –42,74865 | |
| 1,60455 | |
| 19,35391 | |
| 27,00391 | |
| 27,57491 | |
| 17,48019 | |
| 19,13917 | |
| 8,60519 | |
| 15,04109 | |
| –10,75506 | |
| –34,84096 |
Рис. 2.6.7. Результат выполнения «Сезонного Разложения»
(аддитивная модель)
Индексный метод
Задание 2.7.
Имеются данные о производстве продукции и численности работников фирмы по двум филиалам.
Таблица 2.7.1
| Филиалы фирмы | Базовый период | Отчетный период | ||
| Продукция, млн. руб. | Рабочие, чел. | Продукция, млн. руб. | Рабочие, чел. | |
Определить индексы производительности труда постоянного состава, переменного состава и структурных сдвигов.
Выполнение.
Путем вычислений в SPSS можно образовать новые переменные и добавить их в файл данных.
Таким образом, работу со сложными вычислениями можно переложить на компьютер, который сделает ее быстро и, главное, без ошибок.
Для этого поступим для решения рассматриваемой задачи следующим образом
Прежде всего, определим переменные, как представлено на рис. 2.7.1 и введем значения переменных (см. рис. 2.7.2).
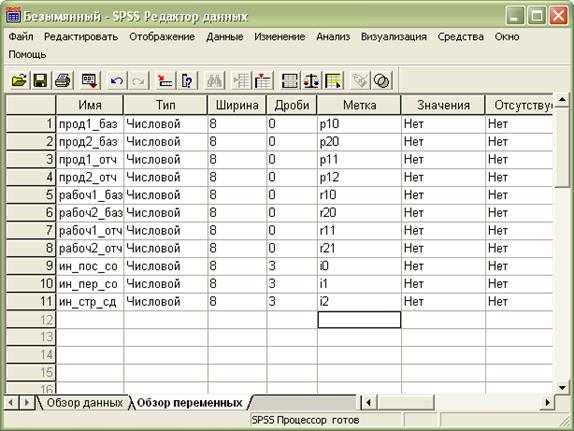
Рис. 2.7.1. Определение переменных
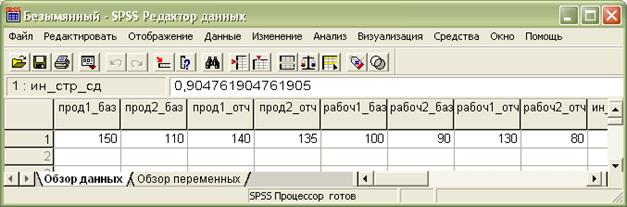
Рис. 2.7.2. Ввод значений переменных
Далее в меню выберем Transform (Изменение) Compute (Просчет).
Откроется диалоговое окно Compute Variable (Вычислить переменную) уже со списком определенных переменных (см. рис. 2.7.3).
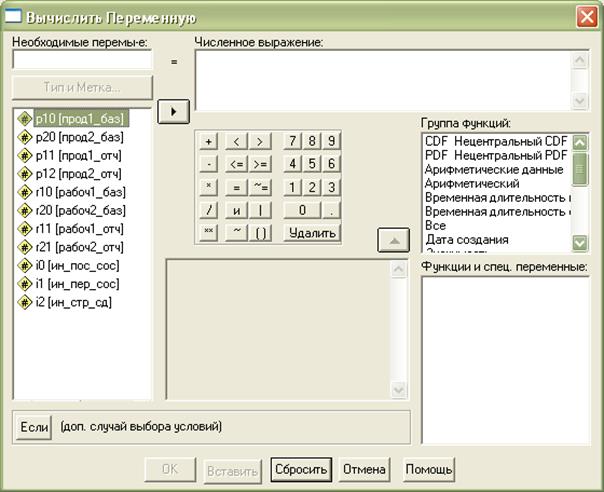
Рис. 2.7.3. Диалоговое окно «Вычислить переменную»
В поле Target Variable (Необходимая переменная) указывается имя переменной, которой присваивается вычисленное значение.
В качестве выходной переменной может служить уже существующая или новая переменная.
В поле Numeric Expression (Численное выражение) вводится выражение, применяемое для определения значения выходной переменной.
В этом выражении могут использоваться имена существующих переменных, константы, арифметические операторы и функции.
Далее в поле Numeric Expression (Численное выражение) создаем выражения для последних трех переменных (индексы производительности труда постоянного состава, переменного состава и структурных сдвигов).
При этом используем функцию SUM из списка справа.
Данные операции представлены на рис. 2.7.4 – 2.7.6.

Рис. 2.7.4. Определение индекса переменного состава
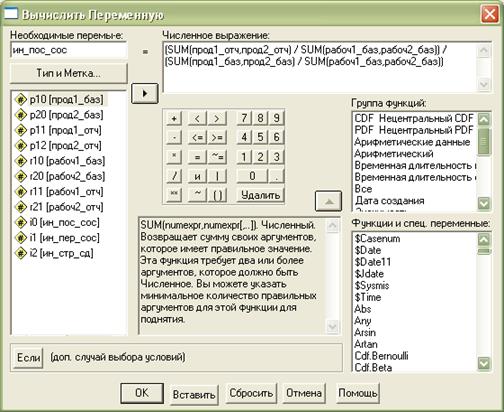
Рис. 2.7.5. Определение индекса постоянного состава
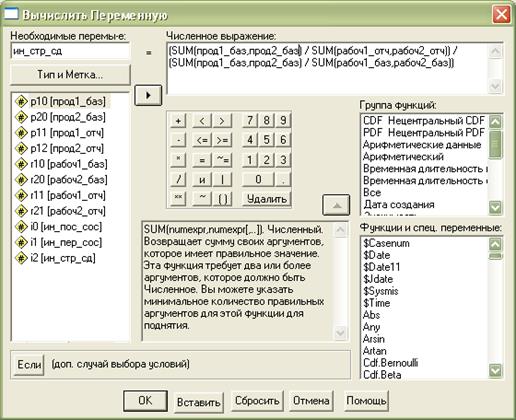
Рис. 2.7.6. Определение индекса структурных сдвигов
Таким образом, вычисляются значения неизвестных индексов (см. рис. 2.7.8).
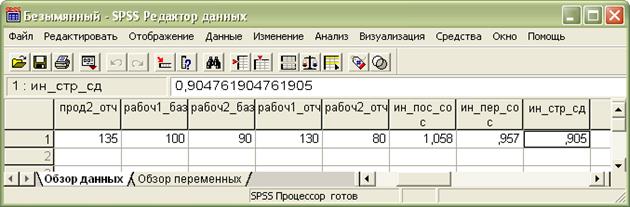
Рис. 2.7.8. Результаты вычисления переменных
Кластерный анализ
Задание 2.8.
Провести кластерный анализ 20 сортов картофеля по двум показателям: процентное содержание крахмала и процентное содержание белка урожайность в нем.
Данные для анализа приведены в таблице 2.8.1.
Таблица 2.8.1
| № п/п | ||||||||||
| Крахмал (%) | 28,6 | 29,4 | 25,3 | 19,4 | 19,6 | 18,8 | 26,9 | 25,7 | 24,6 | 24,7 |
| Белок (%) | 1,6 | 1,5 | 3,2 | 4,5 | 2,8 | 4,4 | 3,2 | 3,3 | 3,4 | |
| № п/п | ||||||||||
| Крахмал (%) | 20,1 | 26,7 | 25,9 | 27,5 | 18,5 | 20,7 | 28,3 | 26,9 | 17,8 | |
| Белок (%) | 2,8 | 1,9 | 1,6 | 4,1 | 2,7 | 1,3 | 4,1 | 4,2 |
Выполнение.
Загрузим файл данных. Проведем простейший кластерный анализ имеющихся данных. Для этого построим диаграмму рассеяния.
· Выберем в меню «Визуализация – Интерактив – Диаграмма рассеяния». Появится диалоговое окно «Диаграмма рассеяния» (рис. 2.8.1). Выбираем «Простой» – «Определ.».
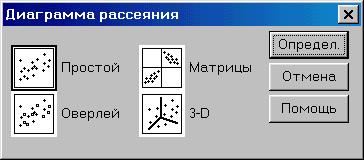
Рис. 2.8.1 Вид диалогового окна «Диаграмма рассеяния»
Появится диалоговое окно «Простой график рассеяния» (рис. 2.8.2).
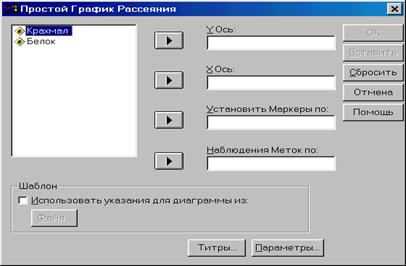
Рис. 2.8.2 Вид диалогового окна «Простой график рассеяния»
· Переменную Белок поместим в поле оси X, а переменную Крахмал в поле оси Y.
· Ничего больше не меняя, начнем расчёт нажатием ОК.
Получим диаграмму рассеяния, представленную на рис. 2.8.3.
При помощи диаграммы рассеяния для двух переменных: Крахмал и Белок, был проведен самый простой кластерный анализ.
Был выбран такой вид графического представления, с помощью которого можно отчётливо распознать группирование в кластеры.
В рассматриваемом случае по виду диаграммы можно увидеть, что наблюдения сгруппировались в четыре кластера.
Далее будем проводить иерархический кластерный анализ.
В иерархических методах каждое наблюдение образовывает сначала свой отдельный кластер.
На первом шаге два соседних кластера объединяются в один; этот процесс может продолжаться до тех пор, пока не останутся только два кластера.
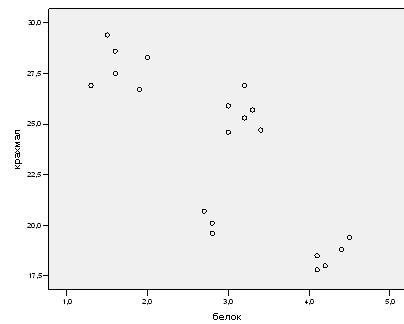
Рис. 2.8.3. Диаграмма рассеяния переменных Крахмал и Белок
Соберём имеющиеся 20 сортов картофеля в кластеры, используя имеющиеся параметры Крахмал и Белок.
Выберем в меню Анализ – Классификация – Иерархический кластерный анализ. Появится диалоговое окно «Иерархический Анализ Кластера» (см. рис. 2.8.4).
Переменные Крахмал и Белок поместите в поле «Переменные».
· Щелчком по выключателю «Статистика» откроем диалоговое окно «Иерархический кластерный анализ: Статистика» (рис. 2.8.5). Оставим флажок напротив опции «Режим накопления». Активируем опцию «Диапазон решений» и введем числа 3 и 5 в качестве границ области. (Хотя на основании графического представления на диаграмме рассеяния (рис. 2.8.3) и ожидается результат в виде четырёх кластеров, но не можем быть полностью уверены в достижении этого результата).
· Вернувшись в главное диалоговое окно, щёлкните по выключателю «Графики». В появившемся диалоговом окне (рис. 2.8.6) активируем опцию вывода «Древовидной диаграммы» и посредством опции «Нет» отмените вывод ориентации графика.
· С помощью кнопки «Метод» возможно выбрать метод образования кластеров, а также метод расчета дистанционной меры и меры подобия соответственно. Здесь (рис. 2.8.7) в поле «Преобразование значений» установите «Множества–z (стандартизацию) значений».
· Вернемся назад в главное диалоговое окно и начните расчёт нажатием ОК.
Рис. 2.8.4. Вид диалогового окна «Иерархический кластерный анализ»
Рис. 2.8.5. Вид диалогового окна
«Иерархический кластерный анализ: Статистики»
Рис. 2.8.6. Вид диалогового окна
«Иерархический кластерный анализ: Диаграммы»
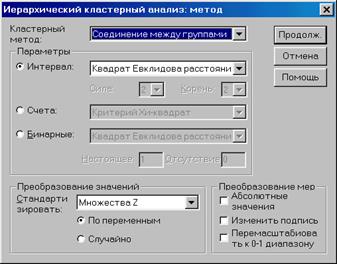
Рис. 2.8.7. Вид диалогового окна
«Иерархический кластерный анализ: Метод»
Вывод основных результатов расчета выглядит следующим образом (рис. 2.8.8).
В таблице Agglomeration Schedule (Порядок агломерации) можно выяснить очерёдность построения кластеров, а также их оптимальное количество.
По двум колонкам, расположенным под общей шапкой Cluster Combined (Объединение в кластеры), можно увидеть, что на первом шаге были объединены наблюдения 19 и 20.
Эти два сорта картофеля максимально похожи друг на друга и отдалены друг от друга очень малое расстояние.
Эти два наблюдения образовывают кластер с номером 1, в то время как кластер 20 в обзорной таблице больше не появляется.
На следующем шаге происходит объединение наблюдений 5 и 11, затем 3 и 8 и т.д.
Под этим коэффициентом подразумевается расстояние между двумя кластерами, определенное на основании выбранной дистанционной меры с учётом предусмотренного преобразования значений.
В нашем случае это квадрат евклидового расстояния, определенный с использованием стандартизованных значений (в примере использовалось Множество–z).
На этом этапе, где эта мера расстояния между двумя кластерами увеличивается скачкообразно, процесс объединения в новые кластеры необходимо остановить, так как в противном случае были бы объединены уже кластеры, находящиеся на относительно большом расстоянии друг от друга.

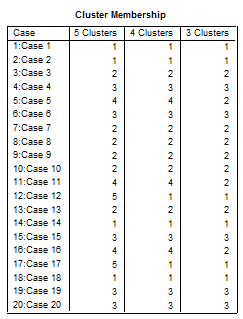

Рис. 2.8.8. Результат выполнения процедуры
Для определения, какое количество кластеров следовало бы считать оптимальным, решающее значение имеет показатель, выводимый под заголовком Coefficients (Коэффициент).
В приведенном примере – это скачок с 0,33 до 2,013. Это означает, что после образования четырех кластеров мы больше не должны производить никаких последующих объединений, а результат с четырьмя кластерами является оптимальным.
Оптимальным считается число кластеров равное разности количества наблюдений (здесь: 20) и количества шагов, после которого коэффициент увеличивается скачкообразно (здесь: 16).
В таблице Cluster Membership (Принадлежность к кластеру) приведена информация о принадлежности каждого наблюдения кластеру, для результатов расчёта содержащих 5, 4 и 3 кластеров.
В заключение приводится затребованная нами древовидная диаграмма, которая визуализирует процесс слияния, приведенный в обзорной таблице порядка агломерации.
Она идентифицирует объединённые кластеры и значения коэффициентов на каждом шаге.
При этом отображаются не исходные значения коэффициентов, а значения, приведенные к шкале от 0 до 25.
Дата добавления: 2022-05-27; просмотров: 216;











