Подсчет критерия Т Вилкоксона

1.Составить список испытуемых в любом порядке, например, алфавит-

ном.

2.Вычислить разность между индивидуальными значениями во втором и первом замерах ("после" - "до"). Определить, что будет считать­ся "типичным" сдвигом и сформулировать соответствующие гипоте­зы.

3.Перевести разности в абсолютные величины и записать их отдель­ным столбцом (иначе трудно отвлечься от знака разности).

4.Проранжировать абсолютные величины разностей, начисляя мень­шему значению меньший ранг. Проверить совпадение полученной суммы рангов с расчетной.

5.Отметить кружками или другими знаками ранги, соответствующие сдвигам в "нетипичном" направлении.

6.Подсчитать сумму этих рангов по формуле:

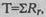
где R_r - ранговые значения сдвигов с более редким знаком.

7. Определить критические значения Т для данного п по Табл. VI Приложения1.ЕслиТ_эмпменьшеилиравенТ_кр,сдвигв "типичную" сторону по интенсивности достоверно преобладает.

3.4. Критерий χ²_r Фридмана

Назначение критерия

Критерий χ²_r применяется для сопоставления показателей, изме­ренных в трех или более условиях на одной и той же выборке испы­туемых.

Критерий позволяет установить, что величины показателей от усло­вия кусловию изменяются, но при этом не указывает на направление изменений.

Описание критерия

Данный критерий является распространением критерия Т Вил­коксона на большее, чем 2, количество условий измерения. Однако здесь мы ранжируем не абсолютные величины сдвигов, а сами индиви­дуальные значения, полученные данным испытуемым в 1, 2, 3 и т. д. замерах.

Например, если у испытуемого в первом замере определена ско­рость прохождения графического лабиринта 54 сек, во втором замере -42 сек, а в третьем замере - 63 сек, то эти показатели получат ранги, соответственно, 2, 1, 3, поскольку меньшему значению, полученному во втором замере, мы начислим ранг 1, среднему значению, полученному в первом замере - ранг 2, а наибольшему значению, полученному в третьем замере - ранг 3.

После того, как все значения будут проранжированы, подсчитыва-ются суммы рангов по столбцам для каждого из произведенных замеров.

Если различия между значениями признака, полученными в раз­ных условиях, случайны, то суммы рангов по разным условиям будут приблизительно равны. Но если значения признака изменяются в раз­ных условиях каким-то закономерным образом, то в одних условиях будут преобладать высокие ранги, а в других - низкие. Суммы рангов будут достоверно различаться между собой. Эмпирическое значение критерия χ²_r и указывает на то, насколько различаются суммы рангов. Чем больше эмпирическое значение χ²_r, тем более существенные рас­хождения сумм рангов оно отражает.

Если χ²_rравняется критическому значению или превышает его, различия статистически Достоверны.

Гипотезы

Н₀: Между показателями, полученными (измеренными) в разных усло­виях, существуют лишь случайные различия.

H₁: Между показателями, полученными в разных условиях, существуют неслучайные различия.