Методы разрешения коллизий

Подобрать совершенную хеш-функцию для заранее неизвестной последовательности крайне трудно, поэтому приходиться мириться с возможными конфликтами. Для разрешения конфликтов используют различные методы, которые разделяют на группу методов с закрытой адресацией и с открытой адресацией. К первой группе относят методы разрешения конфликтов посредством связывания, ко второй – методы с линейным, квадратичным, псевдослучайным зондированием и двойное хеширование.

Разрешение коллизий посредством открытой адресации.В методах данной группы применяются алгоритмы, обеспечивающие перебор элементов таблицы в поисках свободного места для новой записи.

Линейное зондирование. Метод состоит в последовательном переборе элементов таблицы с некоторым фиксированным шагом (рис. 8.4):

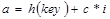
где i – номер попытки разрешить коллизию. Константа 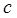задает длину шага. При единичном шаге происходит последовательный перебор всех элементов после текущего.

Рис. 8.4. Линейное зондирование.

С линейным зондированием связана проблема кластеризации. Элементы имеют тенденцию к образованию непрерывных групп, или кластеров, – занятых ячеек. Добавление новых элементов приводит к увеличению размера кластеров. Кластеры влияют на среднее число зондирований, требуемых для обнаружения существующего элемента (попадания) и выяснения отсутствия элемента (промаха). Д.Кнут показал, что среднее число зондирования для обнаружения попадания равно:

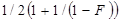
где 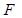– коэффициент загрузки, т.е. количество элементов в таблице, деленное на размер таблицы.

Среднее число зондирований для обнаружения промаха:

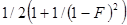
Например, если таблица заполнена примерно наполовину, то для обнаружения попадания потребуется приблизительно 1.5 зондирования, а для обнаружения промаха – 2.5 зондирования. При загрузке 90% эти значения будут уже 5.5 и 55.5 зондирований соответственно. Следовательно, чтобы эффективность оставалась приемлемой для линейного зондирования, загрузка таблицы должна быть на уровне 60%.

Рассмотрим алгоритмы вставки, поиска и удаления элемента при линейном зондировании.

Вставка элемента:

1.

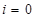
2.

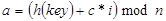
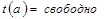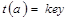3. Если , то , записать элемент, элемент добавлен иначе 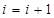, перейти к шагу 2.

Поиск элемента:

1.

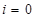
2.

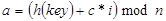
3. Если 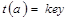, то элемент найден. Если 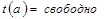, то элемент не найден 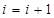, перейти к шагу 2.

Процедура удаления несколько сложнее. Каждый элемент таблицы может находиться в двух состояниях: свободно и занято. Если удалить элемент, переведя его в состояние свободно, то после такого удаления алгоритм поиска будет работать некорректно. Предположим, ключ удаляемого элемента имеет в таблице ключи синонимы. В том случае, если за удаляемым элементом в результате разрешения коллизий были размещены элементы с другими ключами, то поиск этих элементов после удаления всегда будет давать отрицательный результат, так как алгоритм поиска останавливается на первом элементе, находящемся в состоянии свободно.

Скорректировать ситуацию можно различными способами. Самый простой из них заключается в том, чтобы производить поиск элемента не до первого свободного места, а до конца таблицы. Однако такая модификация алгоритма сведет на нет весь выигрыш в ускорении доступа к данным, который достигается в результате хеширования.

Другой способ сводится к тому, чтобы проследить адреса всех ключей-синонимов для ключа удаляемого элемента и при необходимости переразместить соответствующие записи в таблице. Скорость поиска после такой операции не уменьшится, но затраты времени на само переразмещение элементов могут оказаться значительными.

Существует подход, который свободен от перечисленных недостатков. Он состоит в том, что для элементов хеш-таблицы добавляется состояние удалено. Данное состояние в процессе поиска интерпретируется, как занято, а в процессе записи как свободно. Опишем алгоритмы вставки и удаления элемента для таблицы, имеющей три состояния элементов.

Вставка элемента:

1.

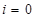
2.

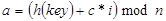
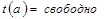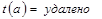3. Если или , то 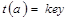, записать элемент, элемент добавлен, иначе 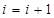, перейти к шагу 2.

Удаление элемента:

1.

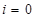
2.

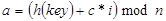
3. Если 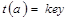, то 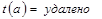, элемент удален. Если 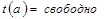, то элемент не найден 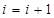, перейти к шагу 2.

Как видно, алгоритм поиска для таблицы, имеющей три состояния, почти не отличается от алгоритма поиска без учета удалений. Разница состоит в том, что при организации самой таблицы необходимо отмечать свободные и удаленные элементы, например, зарезервировав два значения для ключевого поля. Другой вариант реализации может предусматривать введение дополнительного поля, в котором фиксируется состояние элемента. Длина такого поля может составлять всего два бита, что вполне достаточно для фиксации одного из трех состояний.

Слишком частое удаление элементов приведет к появлению большого числа ячеек, отмеченных как удаленные. В свою очередь, это увеличит число зондирований, требуемое для обнаружения попадания или промаха. Если число удаленных ячеек станет слишком большим, желательно выделить новую таблицу и скопировать в нее все элементы.

Однако возможен еще один алгоритм удаления. Удалим элемент и отметим ячейку как свободную. Затем перераспределим все элементы, расположенные в кластере удаленного элемента. Для этого поэлементно будем удалять и вновь вставлять элементы.

Удаление элемента:

1.

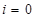
2.

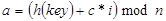
3. Если 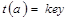, то 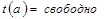, элемент удален. Если 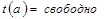, то элемент не найден 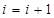, перейти к шагу 2.

4.

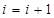
5. Если 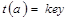, то 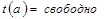, вставить элемент 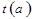, перейти к шагу 5.

Квадратичное зондирование. Метод отличается от линейного тем, что шаг перебора элементов нелинейно зависит от номера попытки найти свободный элемент (рис. 8.5):

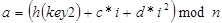
Рис. 8.5. Квадратичное зондирование.

Благодаря нелинейности такой адресации уменьшается число проб при большом числе ключей-синонимов. Однако даже относительно небольшое число проб может быстро привести к выходу за адресное пространство небольшой таблицы вследствие квадратичной зависимости адреса от номера попытки. Кроме того, в отличие от локализованных кластеров при линейном зондировании, здесь возможно появление кластеров, распределенных по всей таблице. Другой серьезный недостаток состоит в том, что квадратичное зондирование не гарантирует посещение всех ячеек.

Двойное хеширование. Метод основан на нелинейной адресации, достигаемой за счет суммирования значений основной и дополнительной хеш-функций (рис. 8.6):

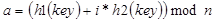
Если первая функция для двух ключей генерирует одинаковый индекс, маловероятно, что вторая функция сгенерирует тот же индекс. Таким образом, два ключа, которые первоначально хешируются в одну ячейку, затем не будут соответствовать одной и той же последовательности зондирования и будет ликвидирована неизбежная кластеризация, сопряженная с линейным зондированием.

Рис. 8.6. Двойное хеширование.

Если размер таблицы равен простому числу, последовательность зондирования обеспечит посещение всех ячеек, прежде чем начнется сначала, что позволит избежать проблем, связанных с квадратичным и псевдослучайным зондированием. При использовании метода вторая функция не должна возвращать 0. Для этого в самой функции хеширования следует выполнить деление по модулю на aTableSize-1 (получить значение в диапазоне 0..aTableSize-2), а затем добавить 1.

Псевдослучайное зондирование. Метод требует использования генератора случайных чисел и заключается в следующем:

1. выполнить хеширование ключа для получения индекса, но не выполнять деление по модулю на размер таблицы;

2. установить начальное значение генератора, равным полученному значению;

3. сгенерировать первое случайное число с плавающей точкой (0..1) и умножить его на aTableSize для получения целочисленного значения в диапазоне (0..aTableSize-1).

В результате будет первая точка зондирования. Если ячейка занята, сгенерировать следующее случайное число, умножить на размер таблицы и вновь выполнить зондирование, пока не обнаружится свободная ячейка.

Метод предотвращает появления кластеров, характерных для линейного метода, однако не гарантирует посещение каждой ячейки таблицы. Вероятность пропуска пустой ячейки достаточно не велика, но вполне возможна, когда таблица заполнена в значительной степени.

Разрешение коллизий посредством закрытой адресации. В методе связывания используются дополнительные ячейки, помимо тех, что требуются хеш-таблице. Сначала с помощью хеш-функции выполняется вычисление индекса, а затем элемент сохраняется в односвязном списке, расположенном в данной ячейке. В случае возникновения коллизии при заполнении таблицы в список для требуемого адреса хеш-таблицы добавляется новый элемент (рис. 8.7).

Для поиска в хеш-таблице вычисляется адрес по значению ключа. Затем выполняется поиск в списке, связанном с вычисленным адресом. Процедура удаления из таблицы сводится к поиску элемента и его удалению из списка.

Существует несколько вариантов вставки элемента в список: поместить элемент в начало списка, в конец списка или упорядочить элементы списка и поместить в соответствующей позиции сортировки. Каждый способ имеют свои преимущества.

Рис. 8.7. Разрешение коллизий методом связных списков.

В первом случае имеет место эффект стека, т.к. последние помещенные элементы будут найдены первыми в случае их поиска. Такой вариант подходит, когда поиск новых элементов будет выполняться чаще поиска старых. Второй способ реализует эффект очереди, когда чаще должны быть востребованы более старые элементы. В последнем случае нет предпочтений, но любой элемент важно найти максимально быстро. Такой способ имеет преимущество только при большом числе элементов. Однако в этом случае желательно расширить таблицу, чем допускать появление большого числа элементов.

При использовании связывания никогда не возникнет ситуации нехватки места. Возможно добавление любого числа элементов в хеш-таблицу и при этом будет происходить только увеличение связных списков. Однако это преимущество имеет и обратную сторону. Проблема заключается в том, длина списков будет расти все больше и больше, и время поиска будет также увеличиваться. Поскольку любая имеющая смысл операция, которую можно выполнить с хеш-таблицами, предполагает поиск, большая часть времени будет тратиться на поиск в связных списках, который реализуется оператором сравнения.

Напомним, для минимизации числа зондирований таблицу следует расширять каждый раз, когда коэффициент загрузки превышает 60%. Каждое сравнение в списке можно рассматривать с позиций зондирования. Идея хеширования и заключается в сведении до минимума числа сравнений.

Для алгоритма связывания коэффициент загрузки по-прежнему может быть вычислен как число элементов, деленное на число ячеек, и может иметь значение большее 1.0 (можно представить средней длиной связных списков, присоединенных к ячейкам таблицы). Для несортированного списка среднее число зондирований для успешного поиска равно F/2, для безрезультатного F. Для отсортированного списка оба значения следует разделить на log₂(F).

Следовательно, несмотря на первую привлекательность применения связных списков, выгода от их использования может быть сведена на нет. В любом случае следует использовать расширение таблицы и эффект стека или очереди при помещении элементов.