Машинное представление графов
Существуют два основных метода представления графов в памяти: матричный (массивами), и связными нелинейными списками. Выбор метода зависит от природы данных и операций, выполняемых над ними. Если задача требует большого числа включений и исключений узлов, то целесообразно представлять граф связными списками. В противном случае можно применить и матричное представление.
При представлении в виде списочной структуры, используется два типа списков – список вершин и список ребер. Элемент списка вершин содержит поле данных и два указателя. Один указатель связывает данный элемент с элементом другой вершины. Второй указатель связывает элемент списка вершин со списком ребер, связанных с данной вершиной.
Для ориентированного графа используют список дуг, исходящих из вершины (рис. 7.3). Элемент списка дуг состоит только из двух указателей. Первый указатель используется для того, чтобы показать в какую вершину дуга входит, а второй – для связи элементов в списке дуг вершины.

а).

б).
Рис. 7.3. Представление графа (а) в виде списочной структуры (б).
Распространенным способом представления графов является матричный способ (рис. 7.4). Для ненаправленных графов обычно используют матрицы смежности, а для ориентированных графов – матрицы инцидентности. Обе матрицы имеют размерность n2, где n – число вершин в графе.
При использовании матриц смежности их элементы представляются в памяти элементами массива. Элемент матрицы имеет ноль в позиции m(i,j), если не существует ребра, связывающего вершину i с вершиной j, или единичное значение в позиции m(i,j), если такое ребро существует:
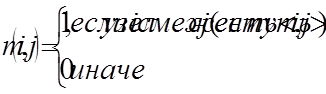
Матрицы смежности применяются, когда в графе много связей и матрица хорошо заполнена. Для простого графа матрица состоит из нулей и единиц, для мультиграфа – из нулей и целых чисел, указывающих кратность соответствующих ребер, для взвешенного графа – из нулей и вещественных чисел, задающих вес каждого ребра.
Матрица смежности симметрична относительно главной диагонали, поэтому можно хранить и обрабатывать только часть матрицы. Для хранения одного элемента матрицы достаточно выделить один бит.
Правила построения матрицы инцидентности аналогичны правилам построения матрицы смежности. Разница состоит в том, что единица в позиции m(i,j) означает выход дуги из вершины i и вход дуги в вершину j.
В некоторых матричных алгоритмах обработки графов используются матрицы путей. Под путем длиной k из вершины i в вершину j будем понимать возможность попасть из вершины i в вершину j за k переходов, каждому из которых соответствует одна дуга. Одна матрица путей mk содержит сведения о наличии всех путей одной длины k в графе. Единичное значение в позиции (i,j) означает наличие пути длины k из вершины i в вершину j:
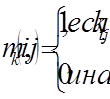
Например, при k=2 имеем (<A,B>,<B,C>).
Примеры построения матриц смежности и инцидентности показаны на рис. 7.14. В первой матрице не отражены направления, поэтому a(i,j) = a(j,i), т.е. матрица симметрична относительно главной диагонали.

Рис. 7.4. Граф и его матричное представление.
Матрица смежности.
| a | b | c | d | e | |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Матрица инцидентности.
| a | b | c | d | e | |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Матрица m1 полностью совпадает с матрицей инцидентности. По матрице m1 можно построить m2 , а по матрице m2 можно построить m3 и т.д. Если граф является ациклическим, то число матриц путей ограничено. В противном случае матрицы будут повторяться до бесконечности с некоторым периодом, связанным с длиной циклов. Матрицы путей не имеет смысла вычислять до бесконечности. Достаточно остановиться в случае повторения матриц.
Матрица путей m1.
| a | b | c | d | e | |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Матрица путей m2.
| a | b | c | d | e | |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Матрица путей m3.
| a | b | c | d | e | |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Если выполнить логическое сложение всех матриц путей, то получим транзитивное замыкание графа (рис. 7.5). В результате матрица будет содержать все возможные пути в графе.
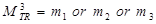

Рис. 7.5. Транзитивное замыкание в графе.
Матрица путей MTR.
| a | b | c | d | e | |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Наличие циклов в графе можно определить с помощью алгоритма, который может быть реализован для матричного и для спискового способа представления графа (рис. 7.6). Принцип выделения циклов следующий. Если вершина имеет только входные или только выходные дуги, то она явно не входит ни в один цикл (обнуляемые строки на первой итерации отмечены курсивом). Можно удалить все такие вершины из графа вместе со связанными с ними дугами.

Рис. 7.6. Определение циклов в графе.
В результате появятся новые вершины, имеющие только входные или выходные дуги. Они также удаляются. Итерации повторяются до тех пор, пока граф не перестанет изменяться. Отсутствие изменений свидетельствует об отсутствии циклов, если все вершины были удалены. Все оставшиеся вершины будут обязательно принадлежать циклам.
Сформулируем алгоритм в матричном виде. Для i от 1 до n выполнить шаги 1-2:
1. если строка M(i ,*) = 0, обнулить столбец i;
2. если столбец M(*, i) = 0, обнулить строку i;
3. если матрица изменилась, выполнить шаг 1;
4. если матрица нулевая завершить процесс, граф ациклический, иначе матрица содержит вершины, входящие в циклы.
Поиск циклов в графе.
| начало | a b c d e f |
| итерация 1 | b c d e f |
| итерация 2 | c d e f |
| итерация 3 | c d e |
| итерация 4 | d e |
| итерация 5 | d e |
Матрица итераций.
| a | b | c | d | e | f | |
| a | ||||||
| b | 1®0 i=1 | 1®0 i=2 | 1®0 i=2 | |||
| c | 1®0 i=3 | 1®0 i=3 | ||||
| d | ||||||
| e | ||||||
| f |
Достоинством алгоритма является то, что одновременно с определением цикличности или ацикличности графа формируется список вершин, входящих в циклы. В матричной реализации после завершения алгоритма остается матрица инцидентности, соответствующая подграфу, содержащему все циклы исходного графа.
Бинарные деревья
С точки зрения представления в памяти различают два типа деревьев: бинарные и сильноветвящиеся. В бинарном дереве из каждой вершины выходит не более двух дуг (рис. 7.7). В сильноветвящемся дереве количество дуг может быть произвольным. Вершины в дереве, имеющие степень ноль, называются листьями.

Рис. 7.7. Бинарное дерево.
Другим признаком структурной классификации бинарных деревьев является полнота и строгость бинарного дерева. Полное бинарное дерево на всех уровнях, меньше n имеют степень узла 2, а на уровне n степень равно 0 (рис. 7.8). Неполное бинарное дерево на уровнях, меньше n может иметь степень узла меньше 2. Строго бинарное дерево состоит только из узлов, имеющих степень два или ноль (рис. 7.9). Не строго бинарное дерево содержит узлы со степенью равной одному.
 |  |
а). б).
Рис. 7.8. Неполное (а) и полное (б) бинарные деревья.
 |  |
а). б).
Рис. 7.9. Строго (а) и не строго (б) бинарные деревья.
Дата добавления: 2021-12-14; просмотров: 451;











