Статические структуры данных
Статические структуры представляют структурированное множество базовых структур. Например, вектор может быть представлен упорядоченным множеством чисел. Статические структуры отличаются отсутствием изменчивости, и память для них выделяется автоматически на этапе компиляции или при выполнении – в момент активизации того программного блока, в котором они определены.
Ряд языков (PL/1, ALGOL-60) допускают размещение статических структур в памяти на этапе выполнения по явному требованию, но и в этом случае объем выделенной памяти остается неизменным до уничтожения структуры. Выделение памяти на этапе компиляции является столь удобным свойством статических структур, что в ряде задач их используют даже для представления объектов, обладающих изменчивостью. Например, когда размер массива неизвестен заранее, для него резервируется максимально возможный размер.
При физическом представлении статической структуре нередко ставится в соответствие дескриптор, или заголовок, который содержит общие сведения о структуре. Дескриптор хранится, как и сама физическая структура, состоит из полей, характер, число и размеры которых зависят от той структуры, которую он описывает и от принятых способов ее обработки.
В ряде случаев дескриптор необходим, т.к. выполнение операции доступа к структуре требует обязательного знания каких-либо ее параметров, которые хранятся в дескрипторе. Другие хранимые в дескрипторе параметры не являются необходимыми, но их использование позволяет сократить время доступа или обеспечить контроль правильности доступа к структуре.
Статические структуры в языках программирования связаны со структурированными типами. Структурированы типы теми средствами интеграции, которые позволяют строить структуры данных произвольной сложности. К таким типам относятся: массивы, записи (в некоторых языках – структуры) и множества (реализованы не во всех языках).
Векторы
Вектор (одномерный массив) – структура данных с фиксированным числом однотипных элементов. Каждый элемент вектора имеет уникальный в рамках заданного вектора номер. Обращение к элементу вектора выполняется по имени вектора и номеру требуемого элемента.
Элементы вектора размещаются в памяти в расположенных подряд (смежных) ячейках. Под элемент вектора выделяется количество байт памяти, определяемое базовым типом элемента вектора. Необходимое число байтов памяти для хранения одного элемента вектора называется слотом. Размер памяти для хранения вектора определяется произведением длины слота на число элементов. В языках программирования вектор представляется одномерным массивом:
< имя >: array [n..k] of < тип >;
где n-номер первого элемента, k-номер последнего элемента.
Представление в памяти вектора показано табл. 4.1. Здесь и далее смещение указано в байтах относительно начального адреса расположения вектора.
Табл. 4.1. Представление вектора в памяти.
| Смещение | +0 | +SizeOf(тип) | … | +(k-n)*SizeOf(тип) |
| Идентификатор | Имя [n] | Имя [n+1] | … | Имя [k] |
В таблице приняты следующие обозначения:
@Имя - адрес вектора (адрес первого элемента вектора);
SizeOf(тип) - размер слота (количество байтов памяти для записи одного элемента вектора);
(k-n)×SizeOf(тип) - относительный адрес элемента с номером k (смещение элемента с номером k).
Пусть объявлен следующий вектор:
var v: array[-2..2] of real;
Представление вектора в памяти показано в табл. 4.2.
Табл. 4.2. Представление вектора v в памяти.
| Смещение | +0 | +6 | +12 | +18 | +24 |
| Идентификатор | v[-2] | v[-1] | v[0] | v[1] | v[2] |
В языках, где память под массив выделяется на этапе компиляции (C, PASCAL, FORTRAN), при описании типа вектора граничные значения индексов должны быть определены. В языках, где память может распределяться динамически (ALGOL, PL/1), значения индексов могут быть заданы во время выполнения программы.
Количество байт непрерывной области памяти, одновременно занятых вектором равно:
ByteSize = (k-n+1)·SizeOf(тип)
Обращение к i-тому элементу вектора выполняется по адресу вектора плюс смещение к данному элементу. Смещение i-ого элемента вектора равно:
ByteNumer = (i-n)·SizeOf(тип)
а его адрес:
@ByteNumber = @имя + ByteNumber
где @имя - адрес первого элемента вектора.
Например:
var v: array[5..10] of Word
Базовый тип элемента вектора Word, поэтому на каждый элемент выделяется по два байта. Смещения элементов относительно @v показано в табл. 4.3.
Табл. 4.3. Представление вектора v.
| Смещение | +0 | +2 | +4 | +6 | +8 | +10 |
| Идентификатор | v[5] | v[6] | v[7] | v[8] | v[9] | v[10] |
Данный вектор будет занимать в памяти: (10-5+1)·2 = 12 байт.
Смещение к элементу вектора с номером 8: (8-5) ·2 = 6.
Адрес элемента с номером 8: @v + 6.
При доступе к вектору задается имя вектора и номер элемента вектора. Адрес i-го элемента может быть вычислен:
@Имя[i] = @Имя+i·SizeOf(тип)-n·SizeOf(тип) (4.1)
Такое вычисление не может быть выполнено на этапе компиляции, т.к. значение переменной i в это время еще неизвестно. Следовательно, вычисление адреса элемента должно производиться на этапе выполнения при каждом обращении к элементу вектора. Для этого, во-первых, должны быть известны параметры формулы (4.1), во-вторых, при каждом обращении должны выполняться две операции умножения и две операции сложения. Преобразовав формулу (4.1), получим:
@Имя[i] = A0+i·SizeOf(тип) (4.2)
где A0 = @Имя-n·SizeOf(тип)
Число хранимых параметров может быть сокращено до двух, а число операций – до одного умножения и одного сложения, т.к. значение A0 может быть вычислено на этапе компиляции и сохранено вместе с SizeOf(тип) в дескрипторе вектора.
Обычно в дескрипторе вектора сохраняются и граничные значения индексов. При каждом обращении к элементу вектора заданное значение сравнивается с граничными и программа аварийно завершается, если заданный индекс выходит за допустимые пределы.
Таким образом, информация, содержащаяся в дескрипторе вектора, позволяет сократить время доступа и обеспечить проверку правильности обращения. Но за эти преимущества приходиться платить быстродействием (обращения к дескриптору) и памятью (размещение самого дескриптора).
В языке C, например, дескриптор вектора отсутствует, точнее, не сохраняется на этапе выполнения. Индексация массивов в C обязательно начинается с нуля. Компилятор каждое обращение к элементу массива заменяет на последовательность команд, реализуя частный случай формулы (4.1) при n = 0.
Массивы
Массив – структура данных, характеризуемая:
- фиксированным набором однотипных элементов;
- каждый элемент имеет уникальный набор значений индексов.
Количество индексов определяют мерность массива, например, два индекса – двумерный массив, три индекса – трехмерный массив, один индекс – одномерный массив или вектор. Обращение к элементу массива выполняется по имени массива и значениям индексов для данного элемента.
Другое определение: массив – вектор, каждый элемент которого – вектор. Синтаксис описания массива представляется в виде:
< Имя >: array[n1..k1] [n2..k2]..[nn..kn] of < Тип >.
Для двумерного массива:
m: array [n1..k1] [n2..k2] of < Тип > или
m: array [n1..k1, n2..k2] of < Тип >
Двумерный массив можно представить в виде таблицы из (k1-n1+1) строк и (k2-n2+1) столбцов. Для двумерного массива, состоящего из (k1-n1+1) строк и (k2-n2+1) столбцов физическая структура представлена в табл. 4.4.
Табл. 4.4. Представление массива m.
| Смещение | +0 | +SizeOf(тип) | … | +(k2-n2)*SizeOf(тип) | ||
| Идентификатор | m[n1,n2] | m[n1,n2+1] | … | m[n1,k2] | ||
| … | ||||||
| m[k1,n2] | m[k1,n2+1] | … | m[n1,k2] | |||
| +(k1-n1)*(k2-n2+1)* SizeOf(тип) | +((k1-n1)*(k2-n2)+1)* SizeOf(тип) | … | +((k1-n1)*(k2-n2+1)+ (k2-n2))*SizeOf(тип) | |||
Многомерные массивы хранятся в непрерывной области памяти. Размер слота определяется базовым типом элемента массива. Количество элементов массива и размер слота определяют размер памяти для хранения массива. Принцип распределения элементов массива в памяти определен языком программирования. Так в языке FORTRAN элементы распределяются по столбцам (быстрее меняется левые индексы), в PASCAL – по строкам (изменение индексов выполняется в направлении справа налево).
Количество байтов памяти, занятых двумерным массивом, определяется по формуле:
ByteSize = (k1-n1+1)·(k2-n2+1)·SizeOf(Тип) (4.3)
Адресом массива является адрес первого байта начального элемента массива.
Смещение элемента массива m[i1,i2] равно:
ByteNumber = [(i1-n1)·(k2-n2+1)+(i2-n2)]·SizeOf(Тип) (4.4)
а его адрес:
@ByteNumber = @m + ByteNumber
Например:
var m: array[3..5][7..8] of Word;
Базовый тип элемента Word требует два байта памяти, тогда таблица смещений элементов массива относительно @m будет следующей как показано в табл. 4.5. Массив будет занимать в памяти: (5-3+1) · (8-7+1) · 2 = 12 байт
адрес элемента m[4,8] равен:
@m+((4-3) · (8-7+1)+(8-7)) · 2 = @m+6
Табл. 4.5. Представление массива m.
| Смещение | Идентификатор |
| +0 | m[3,7] |
| +2 | m[3,8] |
| +4 | m[4,7] |
| +6 | m[4,8] |
| +8 | m[5,7] |
| +10 | m[5,8] |
Таким образом, преимущество использования массивов заключается в быстром вычислении адресов элементов. Независимо от значения элемента, алгоритм вычисления будет одним и тем же. Другими словами, получение доступа к элементу с индексом n принадлежит к классу операций O(1) и не зависит от величины n.
Недостаток массивов связан с ресурсоемкими операциями вставки и удаления элементов. При вставке элемента с индексом i в общем случае следует все элементы с индексами с i по n переместить на одну позицию, чтобы освободить место под новый элемент. Фактически, следует выполнить следующий код:
{ сначала освободить место под новый элемент }
for j:=n downto i do
m[j+1]:=m[j];
{ вставить новый элемент в позицию с индексом i }
m[j]:=a;
{ увеличить значение длины массива на единицу }
Inc(n);
Чем больше количество элементов, тем больше времени потребуется на выполнение операции. Следовательно, операция вставки элемента в массив принадлежит к классу O(i). Та же ситуация и для удаления элемента из массива. Но в этом случае удаление элемента с индексом i означает перемещение всех элементов, начиная с индекса i+1 и до конца массива, на одну позицию к началу массива, чтобы «закрыть» образовавшуюся «дыру». Удаление так же принадлежит к классу O(i).
{ удалить элемент, переместив следующие
за ним элементы на одну позицию вперед }
for j:=i+1 to n do
m[j-1]:=m[j];
{ уменьшить значение длины массива на единицу }
Dec(n);
Открытые массивы. В языке Паскаль доступны для работы массивы открытого типа. Приведем пример объявления открытого массива, элементами которого являются вещественные числа:
var m: array of Real;
В отличие от приведенных выше способов такое объявление не резервирует память под массив, т.к. размеры его заранее не известны. Память будет выделена в процессе выполнения с помощью процедуры SetLength. В следующем примере выделяется память для хранения ста вещественных чисел, индексируемых от 0 до 99:
SetLength(m, 100);
Для массивов открытого типа не следует использовать процедуры управления динамической памятью и символ разыменования «^». Для освобождения памяти, отводимой под открытый массив, переменной следует присвоить значение nil или передать ее в качестве аргумента процедуре Finalize:
Finalize(m);
Процедура линеаризации. Основная операция физического уровня над массивом – доступ к заданному элементу. Как только реализован доступ к элементу, над ним может быть выполнена любая операция, имеющая смысл для типа данных, которому соответствует элемент. Преобразование логической структуры массива в физическую называется процессом линеаризации, в ходе которого многомерная логическая структура преобразуется в одномерную физическую.
В соответствии с формулами (4.3), (4.4) и по аналогии с вектором (4.1), (4.2) для двумерного массива с границами изменения индексов 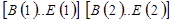 , размещенного в памяти по строкам, адрес элемента с индексами
, размещенного в памяти по строкам, адрес элемента с индексами 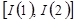 может быть вычислен как:
может быть вычислен как:
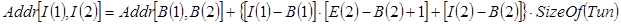 (3.5)
(3.5)
Обобщая (3.5) для массива произвольной размерности 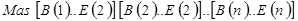 :
:
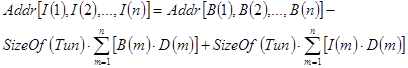 (4.6)
(4.6)
где 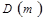 зависит от способа размещения массива.
зависит от способа размещения массива.
При размещении по строкам:
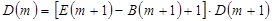 ,
,
где 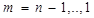 и
и 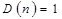
при размещении по столбцам:
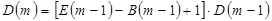 ,
,
где 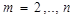 и
и 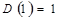 .
.
При вычислении адреса элемента наиболее сложным является вычисление третьей составляющей формулы (4.6), т.к. первые две не зависят от индексов и могут быть вычислены заранее. Для ускорения вычислений множители 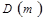 могут быть вычислены заранее и сохраняться в дескрипторе массива.
могут быть вычислены заранее и сохраняться в дескрипторе массива.
Дескриптор массива содержит:
- начальный адрес массива 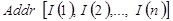 ;
;
- число измерений в массиве n;
- постоянную составляющую формулы линеаризации (первые две составляющие 4.6);
- для каждого из n измерений массива: значения граничных индексов 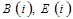 и множитель формулы линеаризации
и множитель формулы линеаризации 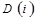 .
.
Специальные массивы. На практике встречаются массивы, которые в силу определенных причин должны записываться в память не полностью, а частично. Это особенно актуально для массивов настолько больших размеров, что для их хранения в полном объеме памяти может быть недостаточно. К таким массивам относятся симметричные и разреженные массивы.
Двумерный массив, в котором количество строк равно количеству столбцов называется квадратной матрицей. Симметричный массив – квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, попарно равны друг другу.
Для симметричной матрицы порядка n в физической структуре достаточно отобразить не n2, а лишь n·(n+1)/2 элементов. В памяти необходимо представить только верхний (включая диагональ) треугольник квадратной логической структуры. Доступ к треугольному массиву организуется таким образом, чтобы можно было обращаться к любому элементу исходной логической структуры, в том числе и к элементам, значения которых хотя и не представлены в памяти, но могут быть определены на основе значений симметричных им элементов.
Для работы с симметричной матрицей должны быть определены процедуры:
- преобразования индексов матрицы в индекс вектора;
- формирования вектора и записи в него элементов верхнего треугольника элементов исходной матрицы;
- получения значения элемента матрицы из ее упакованного представления. Обращение к элементам исходной матрицы выполняется опосредованно, через указанные функции.
Разреженный массив – массив, большинство элементов которого равны между собой, так что хранить в памяти достаточно лишь небольшое число значений отличных от основного (фонового) значения остальных элементов. Различают два типа разреженных массивов:
- массивы, в которых местоположения элементов со значениями, отличными от фоновых, могут быть математически описаны;
- массивы со случайным расположением элементов.
В случае работы с разреженными массивами вопросы размещения их в памяти реализуются на логическом уровне с учетом их типа. К первому типу массивов относятся массивы, у которых местоположения элементов со значениями отличными от фонового, могут быть математически описаны, т.е. в их расположении есть какая-либо закономерность. Элементы, значения которых являются фоновыми, называют нулевыми; элементы, значения которых отличны от фонового, – ненулевыми. Нужно помнить, что фоновое значение не всегда равно нулю.
Ненулевые значения хранятся, как правило, в одномерном массиве, а связь между местоположением в исходном, разреженном, массиве и в новом, одномерном, описывается математически с помощью формулы, преобразующей индексы массива в индексы вектора.
Для работы с разреженным массивом должны быть определены функции:
- преобразования индексов массива в индекс вектора;
- получения значения элемента массива из ее упакованного представления по двум индексам (строка, столбец);
- записи значения элемента массива в ее упакованное представление по двум индексам.
Ко второму типу массивов относятся массивы, у которых местоположения элементов со значениями, отличными от фоновых, не могут быть математически описаны, т.е. в их расположении нет закономерности.
Множества
Множествомназывается неупорядоченная совокупность элементов порядкового типа, элементами которого могут быть величины типов ShortInt, Byte, Char, а также интервального и перечисляемого. Элементы множества могут принимать все значения базового типа, их количество не должно превышать 256. В табл. 4.6 перечислены операции, которые определены над множествами S, S1, S2.
Табл. 4.6. Операции над множествами.
| Обозначение | Название | Результат |
| e in S | Принадлежность элемента e множеству S. | Логический. |
| S1 = S2 | Равенство S1 и S2. | - « - |
| S1 <> S2 | Неравенство S1 и S2. | - « - |
| S1 <= S2 | Включение S1 в S2. | - « - |
| S1 => S2 | Включение S2 в S1. | - « - |
| S1 + S2 | Объединение S1 и S2. | Множество элементов, принадлежащих S1 или S2. |
| S1 - S2 | Разность S1 и S2. | Множество элементов S1, не принадлежащих S2. |
| S1 * S2 | Пересечение S1 и S2. | Множество элементов, принадлежащих S1 и S2. |
В языке Паскаль для задания типа-множества есть зарезервированные слова set и of с помощью которых следует указать элементы множества в виде перечисления или диапазона:
Type
< имя > = set of < тип >;
где
< имя > – идентификатор типа множества;
< тип > – идентификатор или определение типа элементов.
Примеры определения множеств:
Type
TNumber = set of 0..9;
TOperation = set of (Plus, Minus, Mult, Divide);
TSymbols = set of Char;
Тип множества может быть определен и при объявлении переменных:
Var
Symbols: TSymbols;
Operation: TOperation;
Digits: set of 0..9;
Значением переменной-множества может быть любое сочетание элементов, заданных ее типом. Чаще всего значение переменной-множества задается конструктором множества, т.е. перечислением его элементов в квадратных скобках:
Digits:=[1, 3, 5, 7, 9]; { нечетные цифры }
Symbols:=[‘A’..’Z’, ‘a’..’z’]; { латинский алфавит }
Символьные множества хранятся в памяти также как и числовые. Разница лишь в том, что хранятся не числа, а коды ASCII символов. Множество может быть пустым, т.е. не иметь ни одного элемента: Symbols:= [ ].
Множество в памяти хранится как массив битов, в котором каждый бит указывает, является ли элемент принадлежащим объявленному множеству или нет. Число байтов, выделяемых для данных типа множество, вычисляется по формуле:
ByteSize = (max div 8)-(min div 8)+1
где max и min – верхняя и нижняя границы базового типа данного множества.
Номер байта для элемента Е вычисляется по формуле:
ByteNumber = (E div 8)-(min div 8)
а номер бита внутри байта по формуле:
BitNumber = E mod 8
Например, переменная следующего типа:
Type
TVideo = (MDA,CGA,HGC,EGA,EGAm,VGA,VGAm,SVGA,PGA,XGA);
в памяти будет занимать:
ByteSize = (9 div 8)-(0 div 8)+1 = 2 байта
Записи
Запись– конечное упорядоченное множество полей, характеризующихся различным типом данных. Записи являются удобным средством представления программных моделей реальных объектов предметной области, и, как правило, каждый такой объект обладает набором свойств (полей данных), характеризуемых данными различных типов.
Поля записи могут иметь простой или структурный тип. Приведем примеры записей:
Type
{ комплексное число }
Complex = record
Re, Im: Real;
end;
{ календарная дата }
TDate = record
Day: 1..31;
Month: (Jan, Feb, Mar, Apr,May, Jun, Jul, Aug, Sep, Oct, Nov, Dec);
Year: Word;
end;
и затем объявим переменные соответствующего типа:
Var
Z: Complex;
Date: TDate;
Основная операция над записями – доступ к выбранному полю (операция квалификации). Практически во всех языках обозначение этой операции имеет вид:
< имя переменной-записи >.< имя поля >
Например, полям записи Z можно присвоить значения:
Z.Re:=5.2;
Z.Im:=-8.4;
При неоднократном обращении к одному и тому же полю записи или к различным полям одной записи удобно использовать оператор доступа:
with < имя переменной типа запись > do < оператор >
В этом случае можно не указывать имя записи, а только имена полей. С использованием оператора with можно записать:
with Date do
Begin
Day:=18;
Month:=Jan;
Year:=2000;
end;
Большинство языков поддерживает операции, работающие с записью, как с единым целым, а не с отдельными ее полями: операция присваивания одной записи значения другой однотипной записи и сравнения двух однотипных записей на равенство/неравенство. Это позволяет обрабатывать в одной структуре данные разных типов. Например, если переменные A и B представляют собой записи одного типа, то можно использовать присваивание A:=B. При этом поля записи A получат значения соответствующих полей записи B.
В случаях, когда такие операции не поддерживаются языком явно (язык C), они могут выполняться над отдельными полями или записи могут копироваться и сравниваться как неструктурированные области памяти.
Поля записи в свою очередь могут быть записями, т.е. записи могут быть вложенными на несколько уровней. Для доступа к внутренним полям необходимо удлинять составное имя через точку (каждая точка раскрывает один уровень), либо использовать последовательно несколько операторов доступа with.
Пусть определена запись, описывающая некоторый объект:
Type
{ сведения об объекте }
TItem = record
Name: string[20];
Tested: Boolean;
Date: TDate;
end;
Определим переменную типа TItem:
var Item: TItem;
Тогда дата проверки объекта задается составным именем:
Item.Date.Day:=18;
Item.Date.Month:=Jan;
Item.Date.Year:=2000;
или с использованием двух операторов with:
with Item do
with Date do
Begin
Day:=18;
Month:=Jan;
Year:=2000;
end;
Упакованные записи. Доступ к отдельному полю записи эффективен, т.к. величина смещения каждого поля от начала записи постоянна и известна во время компиляции. Так как для поля иногда нужен объем памяти, не кратный размеру слова (или двойного слова), компилятор может «увеличить» запись так, чтобы каждое поле было выровнено по границе слова (или двойного слова), поскольку доступ к невыровненному полю по границе слова (или двойного слова) менее эффективен.
Например, объявление следующего типа:
TSomeStruct = record
c1: Char; { 1 байт, пропустить 1 байт }
w1: Word; { 2 байта }
c2: Char; { 1 байт, пропустить 1 байт }
w2: Word; { 2 байта }
end;
приведет к выделению четырех слов для каждой записи таким образом, чтобы поля были выровнены по границе слова, в то время как следующее объявление экономит память:
TSomeStruct = record
w1: Word; { 2 байта }
w2: Word; { 2 байта }
c1: Char; { 1 байт, пропустить 1 байт }
c2: Char; { 1 байт, пропустить 1 байт }
end;
По умолчанию для быстрого доступа элементы массива и поля записей выравниваются по границе слова или двойного слова. Для устранения такого выравнивания можно использовать зарезервированное слово packed перед словом record или array. Это приведет к снижению скорости доступа, но одновременно уменьшит объем занимаемой структурой места в памяти.
Полем записи может быть другая запись, но не такая же, что связано, прежде всего, с тем, что компилятор должен выделить для размещения записи память.
Пусть, определена запись вида:
Rec = record
f1: Word;
f2: Char;
f3: Rec;
end;
Для поля f1 будет выделено 2 байта, для поля f2 – 1 байт, а поле f3 – запись, которая в свою очередь состоит из f1 (2 байта), f2 (1 байт) и f3 и т.д. Компилятор, встретив подобное описание, выдает сообщение о нехватке памяти. Однако полем записи вполне может быть указатель на другую такую же запись: размер памяти, занимаемый указателем известен, и проблем с выделением памяти не возникает. Подобный прием широко используется для установления связей между однотипными записями.
PRec = ^Rec
Rec = record
f1: Word;
f2: Char;
f3: PRec;
end;
Записи с вариантами. В ряде прикладных задач можно столкнуться с группами объектов, чьи наборы свойств перекрываются лишь частично. Обработка таких объектов производится по одним и тем же алгоритмам, если обрабатываются общие свойства объектов, или по разным – если обрабатываются специфические свойства.
Можно описать все группы единообразно, включив в описание все наборы свойств для всех групп, но такое описание будет неэкономичным с точки зрения расходуемой памяти и неудобным с логической точки зрения. Если же описать каждую группу собственной структурой, теряется возможность обрабатывать общие свойства по единым алгоритмам.
Для задач подобного рода некоторые языки программирования (C, PASCAL) предоставляют записи с вариантами. Запись с вариантами состоит из двух частей. В первой части описываются поля, общие для всех групп объектов, моделируемых записью. Среди полей обычно бывает поле, значение которого позволяет идентифицировать группу, к которой данный объект принадлежит и, следовательно, какой из вариантов второй части записи должен быть использован при обработке.
Вторая часть записи содержит описания непересекающихся свойств – для каждого подмножества таких свойств – отдельное описание. Язык программирования может требовать, чтобы имена полей-свойств не повторялись в разных вариантах (PASCAL), или же требовать именования каждого варианта (C). В первом случае идентификация поля, находящегося в вариантной части записи при обращении к нему ничем не отличается от случая простой записи:
< имя переменной-записи >.< имя поля >
Во втором случае идентификация немного усложняется:
< имя переменной-записи >.< имя варианта >.< имя поля >
Рассмотрим использование записей с вариантами. Пусть требуется размещать на экране простые геометрические фигуры – круги, прямоугольники, треугольники. Для «базы данных», которая будет описывать состояние экрана, удобно представлять все фигуры однотипными записями.
Для любой фигуры описание должно включать координаты некоторой опорной точки (центра, правого верхнего угла, одной из вершин) и код цвета. Другие параметры построения будут разными для разных фигур: для круга – радиус; для прямоугольника – длины непараллельных сторон; для треугольника – координаты двух других вершин. Запись с вариантами для такой задачи в языке PASCAL выглядит так:
figure = record
ftype : Char; { тип фигуры }
x0, y0 : Word; { координаты опорной точки }
color : Byte; { цвет }
case fig_t: Char of
'C': (radius: Word); { радиус окружности }
'R': (len1, len2: Word); { длины сторон прямоугольника }
'T': (x1,y1,x2,y2: Word); { координаты двух вершин }
end;
Если определена переменная fig1 типа figure, в которой хранится описание окружности, то обращение к радиусу этой окружности будет иметь вид: fig1.radius. Поле с именем fig_type введено для представления идентификатора вида фигуры, который, например, может кодироваться символами: «C» – окружность или «R» – прямоугольник, или «T» – треугольник.
Выделение памяти для записи с вариантами показано на рис. 4.1. Под запись с вариантами выделяется объем памяти, достаточный для размещения самого большого варианта. Если выделенная память используется для меньшего варианта, часть ее остается неиспользуемой. Общая для всех вариантов часть записи размещается так, чтобы смещения всех полей относительно начала записи были одинаковыми для всех вариантов.
Наиболее просто это достигается размещением общих полей в начале записи, но это не строго обязательно. Вариантная часть может и «вклиниваться» между полями общей части. Поскольку в любом случае вариантная часть имеет фиксированный (максимальный) размер, смещения полей общей части также останутся фиксированными.

Рис. 4.1. Выделение памяти для записи с вариантами.
Таблицы
В предыдущем разделе было отмечено, что полями записи могут быть интегрированные структуры – векторы, массивы, другие записи. Аналогично элементами векторов и массивов могут быть также интегрированные структуры. Одна из таких структур – таблица. С логической точки зрения таблица представляет вектор, элементами которого являются записи. Таблицы не имеют стандартного типа данных в языке Паскаль.
В таблицах доступ к элементам производится не по номеру (индексу), а по ключу – значению одного из свойств объекта, описываемого записью-элементом таблицы. Ключ идентифицирует данную запись во множестве однотипных. К ключу предъявляется требование уникальности в данной таблице. Ключ может включаться в состав записи и быть одним из ее полей, но может и не включаться, а вычисляться по положению записи. Таблица может иметь один или несколько ключей. Например, при интеграции в таблицу записей о студентах выборка может производиться как по личному номеру студента, так и по фамилии.
Основной операцией при работе с таблицами является операция доступа к записи по ключу. Она реализуется процедурой поиска. Поскольку поиск может быть значительно более эффективным в таблицах, упорядоченных по значениям ключей, довольно часто над таблицами необходимо выполнять операции сортировки. Такие операции рассматриваются в разделе 4.6.
Различают таблицы с фиксированной и переменной длиной записи. Очевидно, что таблицы, объединяющие записи идентичных типов, будут иметь фиксированные длины записей. Необходимость в переменной длине может возникнуть в задачах, подобных тем, которые рассматривались для записей с вариантами. Как правило, таблицы для таких задач и составляются из записей с вариантами, т.е. сводятся к фиксированной (максимальной) длине записи.
Значительно реже встречаются таблицы с действительно переменной длиной записи. Хотя в таких таблицах и экономится память, но возможности работы с такими таблицами ограничены, т.к. по номеру записи невозможно определить ее адрес. Таблицы с записями переменной длины обрабатываются только последовательно – в порядке возрастания номеров записей.
Доступ к элементу такой таблицы обычно осуществляется в два шага. На первом шаге выбирается постоянная часть записи, в которой содержится (в явном или неявном виде) длина записи. На втором шаге выбирается переменная часть записи в соответствии с ее длиной. Прибавив к адресу текущей записи ее длину, получают адрес следующей записи.
Дата добавления: 2021-12-14; просмотров: 530;











