Полевые способы определения сжимаемости пород
В полевыхусловиях для определения сжимаемости пород на испытуемую породу в шурфе и скважине посредством штампа передают статическую нагрузку, постепенно возрастающую во времени. Под действием этой нагрузки порода испытывает три фазы деформации.
1. Фаза уплотнения, в процессе которой происходит деформации сжатия породы непосредственно под штампом в виде колонки. Окружающая колонку порода не подвергается деформации. Эта фаза характеризуется линейной зависимостью между нагрузкой и деформацией (отрезок ОА на графике стадий деформации породы под нагрузкой, рис. 8.2).
2. Фаза сдвига, в процессе которой нарушается линейная зависимость между нагрузкой и деформацией. Приращение деформации опережает увеличение нагрузок, отдельные участки породы начинают сдвигаться относительно друг друга, наступает состояние предельного равновесия массива породы, окружающей сжимаемую колонку (отрезок АБ на графике рис. 8.2).
3. Стадия разрушения, в процессе которой происходит резкое увеличение деформаций, разрушение породы в массиве, непосредственно окружающем сжимаемую колонку, и выпирание породы вверх. Нагрузка, соответствующая началу этого процесса, называется пределом несущей способности.
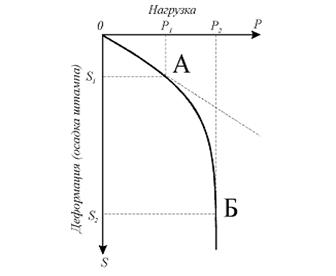
Рис. 8.2 Стадии деформации породы под нагрузкой штампом
Для обеспечения устойчивости породы под сооружением его давление не должно превышать давления, отвечающего конечному периоду первой стадии деформаций, т. е. давления Р1 на графике (рис. 8.2). Это давление называется предельным, или критической нагрузкой, а внутреннее сопротивление породы сжатию, соответствующее этой нагрузке, — несущей способностью. Кроме критической нагрузки и несущей способности по результатам опытов определяют модуль общей деформации, который для прямолинейного участка графика S = f(P) рассчитывается по формуле
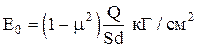
где Q — полная нагрузка на штамп, кГ;
S — конечная осадка штампа, отвечающая нагрузке Q, см,
d — диаметр штампа или круга, равновеликого площади штампа квадратного или прямоугольного сечения; m—коэффициент поперечного расширения (коэффициент Пуассона), принимаемый для песков и супесей равным 0,30, для суглинков — 0,35 и для глин — 0,40.
Существует много конструкций установок для испытания пород пробными нагрузками в шурфах или скважинах. Основной деталью этих установок является штамп, с помощью которого на породу передается давление. В России принят стандартный штамп квадратной формы площадью 5000 см2 для испытаний в шурфах. Для испытаний в скважинах применяется штамп площадью 600 см2. Штамп обычно представляет собой толстую стальную плиту, усиленную ребрами жесткости. Остальные детали установок служат для передачи давления на плиту.
Для измерения осадок применяются специальные приборы: прогибомеры и нивелиры.
На штамп, установленный на необходимой глубине в шурфе или скважине, передается давление ступенями 0,25—0,5 кГ/см2, и производятся наблюдения за осадкой штампа. Давление увеличивается по мере затухания деформаций от предыдущей ступени. Общее давление доводится в слабых породах до разрушающего (третья фаза деформаций), а в плотных породах — до предельного (вторая фаза деформаций).
По наблюдениям за осадкой штампа строят график зависимости осадки штампа от времени. По результатам опытной нагрузки составляют график зависимости осадки от давления, при этом осадки штампа откладывают на период начала приложения данного давления и на период условной стабилизации при этом давлении. В силу этого график получается ступенчатым (рис. 8.3). Точка А на графике считается критической точкой перегиба, отделяющей начально-прямолинейный участок графика от участка, где зависимость между осадками и давлением выражается кривой.
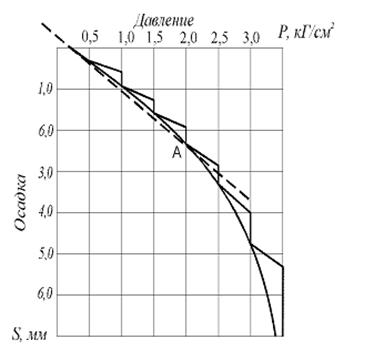
Рис.8.3 График зависимости осадки штампа от давления
Следует отметить, что величины модуля общей деформации, определенные для одной и той же породы лабораторным способом и полевым, отличаются друг от друга. Модуль деформации, получаемый по данным лабораторных исследований, обычно значительно меньше значения модуля деформации, определяемого для той же породы по полевым опытным нагрузкам..
В последнее время для определения модуля деформации пород в скважинах стала применяться прессиометрия. Сущность этого способа заключается в том, что в буровую скважину на необходимую глубину опускают эластичную камеру, заполненную водой. После этого при помощи сжатого воздуха создают в этой камере давление и замеряют деформации ее. Изменив несколько раз давление, получают ряд наблюдений за деформациями. По данным этих наблюдений рассчитывается модуль деформации.
Весьма перспективным для определения физических свойств прочности и деформационных свойств пород является также пенетрационно-каротажные методы, разрабатываемые Всесоюзным научно-исследовательским институтом гидрогеологии и инженерной геологии. Суть их заключается в изучении сопротивления проникновению в толщу породы зондов-датчиков, вдавливаемых специальными гидравлическими установками на глубину до 25 м. Одновременно с определением этого сопротивления производится комплекс модификаций радиоактивного каротажа. В результате получают непрерывную информацию о составе, свойствах и состоянии пород в виде диаграмм. Комплексная интерпретация этих данных позволяет получить необходимые расчетные данные для проектирования оснований сооружений без бурения скважин и лабораторных исследований образцов пород.
9.ПРОЧНОСТЬ ГОРНЫХ ПОРОД И ГРУНТОВ
(сопротивление пород сдвигу)
Явление нарушения прочности грунтов нагляднее всего демонстрирует процесс одноосного сжатия.
В отличие от компрессии процесс одноосного сжатия заключается в том, что образец изучаемой породы помещается под пресс и подвергается действию внешней вертикальной нагрузки в условиях свободного расширения в стороны до момента разрушения.
Эксперименты по разрушению цилиндра образца из различных грунтов дают следующую картину:
1. Плотные пески разрушаются в результате сдвига одной части образца относительно другой. Сдвиг происходит по четко выраженной плоскости, наклоненной к оси действующего вертикального напряжения под углом, не превышающим 450.
2. Рыхлые пески не имеют явно выраженной плоскости среды. Разрушение происходит в результате взаимных перемещений (сдвигов зерен) внутри образца, которые принимает характерную форму бочки. Интенсивность деформации нарастает непрерывно, нет явно выраженной критической точки разрушения.
3. Разрушение твердых и тугопластичных глинистых грунтов внешне напоминает сдвиг в образцах грунта из плотных песков. Однако, существует ярко выраженная критическая точка в процессе нарастания интенсивности деформации, когда происходит скол образца по одной или нескольким плоскостям, расположенным под углом действующего внешнего напряжения, причем этот угол для глин больше, чем для песков.
4. В мягкопластичных глинах можно проследить четкие плоскости сдвига, но в этом случае происходит перемещение одной части образца относительно другой без нарушения сплошности.
Несмотря на различие в характере процесса разрушения для различных типов грунтов, наблюдается общая закономерность.
Потеря прочности наступает в результате сдвига одной части грунта по плоскости скольжения относительно другой. Сдвиг возникает тогда, когда возникают касательные напряжения, превышающие некоторое предельное значение, т.е. когда касательные напряжения, возникающие на плоскости сдвига, превышают силы сопротивления грунта этому напряжению - сдвигу. Характерным примером такой плоскости сдвига при нарушении прочности грунта является плоскость скольжения оползня.
Экспериментально установлено, что в момент перехода от равновесия к разрушению, т.е. существует следующая зависимость между сопротивлением грунта сдвигу t (касательным напряжением) и напряжениями, нормальными к поверхности сдвига dn.
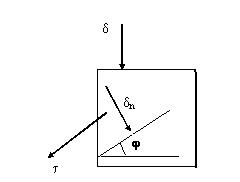
t = dntgj + c
dn - нормальное внешнее давление;
t - сдвигающее усилие, увеличиваемое до предельного, при котором происходит разрушение образца.
Эта зависимость была экспериментально установлена в XVIII веке Кулоном и выражает условие прочности грунтов.
Экспериментальное изучение явления прочности пород и характеристик с и j происходит в сдвиговых приборах. Схема опыта на сдвиг представлена на рисунке:
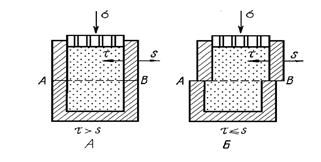
Рис. 9.1 Схема опыта на сдвиг.
Опыт проводится на нескольких образцах:
dn1 ® t1 dn2 ® t2 dn3 ® t3
Срезающее (сдвигающее) усилие t в глинистых породах зависит от нормальной нагрузки и увеличивается при ее росте за счет сближения частиц между собой в результате деформаций и в то же время сопротивление пород сдвигу тем больше, чем больше связность частиц между собой.
По результатам испытаний строится график сопротивления породы сдвигу.
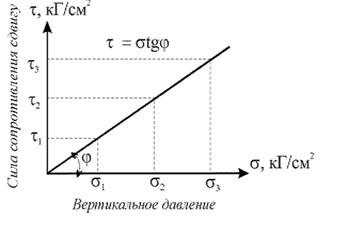
Рис. 9.2 График сопротивления сдвигу песчаной породы
t
 j
j
c { σ
t = dntgj + c
Рис. 9.3 График сопротивления пород сдвигу глинистой породы j - угол внутреннего трения; с - сцепление.
Эта закономерность является вторым основным законом механики грунтов, который формулируется следующим образом:
Сопротивление пород сдвигу (t) находится в прямой зависимости от нормальных напряжений, возникающих за счет приложения внешней нагрузки. Силы сопротивления пород сдвигу возникают за счет сил трения, возникающих между частицами, с, tgj - характеристики этого явления.
Величина с рассматривается, как сцепление, вызванное силами связи внутри грунта (водно-коллоидные, кристаллизационные, цементация).
Если соединить каждую отдельную экспериментальную точку с началом координат, получим прямые линии, угол наклона которых к оси абсцисс называется углом сдвига y,
tg y - коэффициент сдвига. Fp = 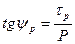 ,
,
sс - всесторонее внутреннее давление связности sс = с/ tgj = c · ctg j.
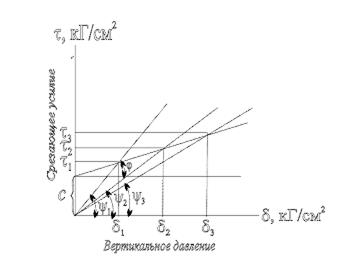
Рис. 9.4 Углы сдвига на графике сопротивления сдвигу связной породы
9.1 Определение сопротивляемости грунтов сдвигу по данным лабораторных испытаний
Задача 8.
Для установления допустимой нагрузки на глинистый грунт в основании подпорной стенки необходимо определить значения угла внутреннего трения φ и общего сцепления с, отвечающие его природной влажности w =21%.
Испытания образцов с ненарушенной структурой на сдвиговом приборе (без предварительного обжатия образцов под нагрузкой в целях сохранения грунтом природной влажности) дали следующие результаты сопротивляемости сдвигу (удельное сопротивление сдвигу) τ.
1. при вертикальной нагрузке р1 = 1 кГ/см2 τ = 0.81 кГ/см2
2. при вертикальной нагрузке р1 = 2 кГ/см2 τ = 1.17 кГ/см2
3. при вертикальной нагрузке р1 = 3 кГ/см2 τ = 1.48 кГ/см2.
Решение.
Выражение для определения сопротивляемости грунта сдвигу глинистого грунта имеет вид: τ = p tgφ + c . Строим график зависимости τ =f (p):
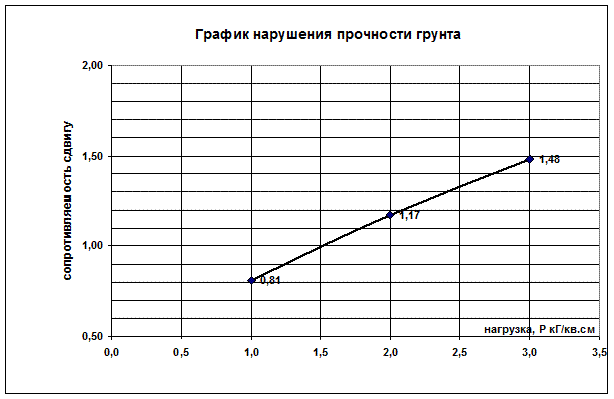
Рис. 9.5 График сопротивляемости породы сдвигу по данным испытаний
на сдвиговом приборе.
Определяем угол внутреннего трения φ .
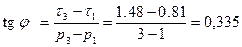 , φ= 18°.
, φ= 18°.
Находим величину общего сцепления c = τ - p tgφ
с = 0.81-0.335 ∙ 1.0 = 0.475 кГ/см2 ≈ 0.48 кГ/см2.
Таким образом, для данного подвергнутого испытанию глинистого грунта при его природной влажности w =21%
угол внутреннего трения φ= 18°, общее сцепление с = 0.48 кГ/см2.
Задача 9.
Для определения заложения откосов насыпи необходимо определить расчетные характеристики сопротивляемости сдвигу φи с суглинистого пылеватого грунта с нарушенной структурой при разных условиях его увлажнения, определяемых следующими значениями влажности грунта:
W1 =15%, W 2 =20%, W3 =25%, W4 =30%, W 5=35%, W 5=40%.
С этой целью были произведены испытания образцов с нарушенной структурой на сдвиговом приборе под разными нагрузками р с различной длительностью эксперимента и одновременным определением влажности грунта из зоны сдвига.
В результате проведенных опытов были получены следующие значения влажности грунта w и отвечающие им величины сопротивления грунта сдвигу τпри разных нагрузках р.
Таблица 9.1
Результаты испытаний образцов суглинистого пылеватого грунта с нарушенной структурой на сдвиговом приборе.
| р1= 1кГ/см2 | w % | ||||||||||
| τpw кГ/с2 | 1,51 | 1,10 | 0,88 | 0,82 | 0,65 | 0,51 | 0,46 | 0,43 | 0,35 | 0,32 | |
| Р2= 2кГ/см2 | w % | ||||||||||
| τpw кГ/с2 | 2,10 | 1,5 | 1,27 | 1,02 | 0,92 | 0,88 | 0,79 | 0,71 | 0,58 | ||
| Р3= 3кГ/см2 | w % | ||||||||||
| τpw кГ/с2 | 2,45 | 1,94 | 1,50 | 1,25 | 1,13 | 1,07 | 1,01 | 0,88 |
Решение.
Сопротивляемость грунта сдвигу определяется выражением: τpw = p tgφ + cw.
Необходимо построить графики
1. τpw = f1(w) для каждого из значений p
2. τpw = f2 (p) для каждого из значений w.
Сопротивляемость сдвигу τpw глинистого грунта имеет следующий вид:
· В зависимости от влажности - для различных значений нагрузки:
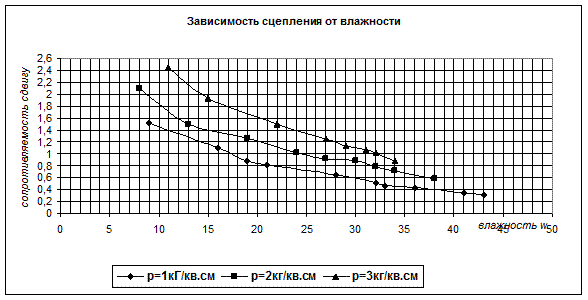
Рис. 9.6 График зависимости сцепления с от влажности
В зависимости от нагрузки - для различных значений влажности:
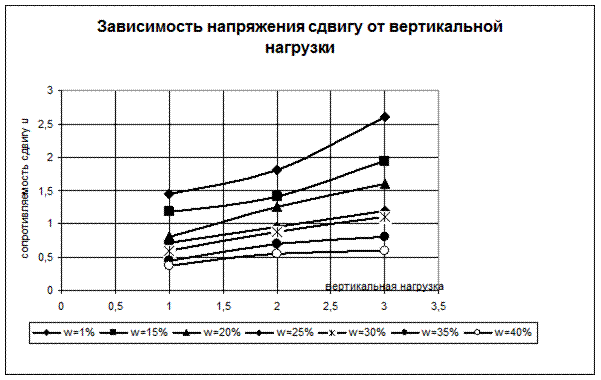
Рис. 9.7 График зависимости сопротивляемости сдвигу τpw от вертикальной нагрузки
Снимая с графиков соответствующие величины p и τpw для требуемых значений влажности, получаем таблицу и строим соответствующие графики:
Таблица 9.2
Таблица для построения диаграмм сдвига τpw =f(p) для заданных значений влажности
| w=10% | p | τ | w=15% | p | τ | w=20% | p | τ | w=25% | p | τ |
| 1,45 | 1,18 | 0,8 | 0,72 | ||||||||
| 1,8 | 1,4 | 1,25 | 0,95 | ||||||||
| 2,6 | 1,94 | 1,6 | 1,2 | ||||||||
| w=30% | p | τ | w=35% | p | τ | w=40% | p | τ | |||
| 0,6 | 0,45 | 0,38 | |||||||||
| 0,88 | 0,7 | 0,55 | |||||||||
| 1,1 | 0,8 | 0,6 |
Самостоятельно:
· Определить угол внутреннего трения и сцепление в зависимости от влажности.
· Построить графики зависимости угла внутреннего трения и сцепления в зависимости от влажности.
10. ОПРЕДЕЛЕНИЕ НОРМАТИВНЫХ И РАСЧЕТНЫХ ХАРАКТЕРИСТИК ГРУНТОВ.
Нормативные значения всех параметров грунта, кроме значений угла внутреннего трения и удельного сцепления, по ГОСТ 20522-75 определяются как среднее арифметическое результатов частных (отдельных) определений данного параметра физико-механических свойств грунта. За нормативное значение удельного сцепления и угла внутреннего трения принимают параметры прямолинейной зависимости сдвиговых усилий от вертикального давления, рассчитанные по методу наименьших квадратов.
Расчетные значенияхарактеристик грунтаХопределяются по формуле
X=Xn/gg,
где Xn - нормативное значение характеристики,
gg – коэффициент надежности (безопасности) по грунту.
Коэффициент безопасности по грунту вычисляют по формуле:
gg= 1/(1±r),
где r - показатель точности оценки среднего значения характеристики, определяемый по зависимостям:
для C и tg j : r = ta V,
для остальных характеристик : 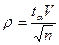 ,
,
где n – количество частных значений отдельной характеристики,
V – коэффициент вариации,
Для расчета коэффициента вариации V определяют нормативное значение характеристики Хn и ее среднеквадратичное отклонение s :
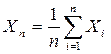 ;
; 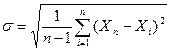 ;
; 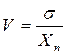 ,
,
Xi – частные значения характеристики, n – количество определений.
Нормативные значения tgj n и c n рассчитывают по формулам:
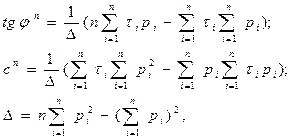
где ti и pi -частные определения сопротивления срезу и нормального давления,
n – число определений величины t.
Среднеквадратичное отклонение для с и j рассчитываются по формулам:
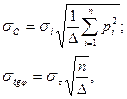
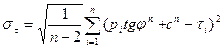 .
.
ta - принимается по таблице (ГОСТ 20522-75 ) в зависимости от заданной доверительной вероятности a для числа степеней свободы К:
для C и tg j : К =n-2
для остальных характеристик : К = n-1
Доверительная вероятность a при определении расчетных характеристик грунтов принимается
· при расчете оснований по несущей способности a=0.95,
· при расчете оснований по деформациям a=0.85
Для каждого выделенного на разрезе инженерно-геологического элемента количество одноименных частных определений должно быть не меньше шести.Для модуля общей деформации грунтов, определяемого в полевых условиях штампом, можно ограничиться тремя или двумя испытаниями,если они отклоняются от среднегоне более чем на 25%.
Таблица 10.1
Значения коэффициента ta
| Число степеней свободы К | Значения коэффициента ta при односторонней доверительной вероятности a, равной | |||||
| 0,85 | 0,90 | 0,95 | 0,975 | 0,98 | 0,99 | |
| 1,25 | 1,64 | 2,35 | 3,18 | 3,45 | 4,54 | |
| 1,19 | 1,53 | 2,13 | 2,78 | 3,02 | 3,75 | |
| 1,16 | 1,48 | 2,01 | 2,57 | 2,74 | 3,36 | |
| 1,13 | 1,44 | 1,94 | 2,45 | 2,63 | 3,14 | |
| 1,12 | 1,41 | 1,90 | 2,37 | 2,54 | 3,00 | |
| 1,11 | 1,40 | 1,86 | 2,31 | 2,49 | 2,90 | |
| 1,10 | 1,38 | 1,83 | 2,26 | 2,44 | 2,82 | |
| 1,10 | 1,37 | 1,81 | 2,23 | 2,40 | 2,76 | |
| 1,09 | 1,36 | 1,80 | 2,20 | 2,36 | 2,72 | |
| 1,08 | 1,36 | 1,78 | 2,18 | 2,33 | 2,68 | |
| 1,08 | 1,35 | 1,77 | 2,16 | 2,30 | 2,65 | |
| 1,08 | 1,34 | 1,76 | 2,15 | 2,28 | 2,62 | |
| 1,07 | 1,34 | 1,75 | 2,13 | 2,27 | 2,60 | |
| 1,07 | 1,34 | 1,75 | 2,12 | 2,26 | 2,58 | |
| 1,07 | 1,33 | 1,74 | 2,11 | 2,25 | 2,57 | |
| 1,07 | 1,33 | 1,73 | 2,10 | 2,24 | 2,55 | |
| 1,07 | 1,33 | 1,73 | 2,09 | 2,23 | 2,54 | |
| 1,06 | 1,32 | 1,72 | 2,09 | 2,22 | 2,53 | |
| 1,06 | 1,32 | 1,71 | 2,03 | 2,19 | 2,49 | |
| 1,05 | 1,31 | 1,70 | 2,04 | 2,17 | 2,46 | |
| 1,05 | 1,30 | 1,68 | 2,02 | 2,14 | 2,42 | |
| 1,05 | 1,30 | 1,67 | 2,00 | 2,12 | 2,39 | |
| Число степеней | Значения коэффициента ta при двухсторонней доверительной вероятности a, равной | |||||
| свободы К | 0,70 | 0,80 | 0,90 | 0,95 | 0,96 | 0,98 |
Задача 10.
Определить расчетную характеристику удельного веса грунта gn для оценки несущей способности при следующих частных значениях gi: 18,7, 20,4, 19,2, 19,8, 18,2, 17,8 кН/м3.
1. Вычисляемнормативное значение gn для n=6:
 ,
,
2. Величина среднего квадратичного отклонения s: 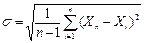 =
= 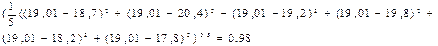
3. Коэффициент вариации V = 0.98/19,01 = 0,05.
4. Показатель точности оценки среднего значения характеристики r 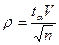 :
:
tga=2,13 при a=0,95 и К=4 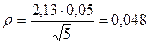 ;
;
5. Коэффициент безопасности по грунту gg= 1/(1±r) = 1 / (1-0,048) = 1,05
6. Расчетная характеристика удельного веса грунта X(g)=Xn/gg =19,01/1,05=
=18,1 кН/м3
Задача 11.
Определить расчетные характеристики сопротивления грунта сдвигу для расчета по деформациям при следующих экспериментальных данных:
| i | Pi МПа | ti МПа | Pi МПа | ti МПа |
| 0,1 | 0,14 | 0,1 | 0,16 | |
| 0,2 | 0,18 | 0,2 | 0,19 | |
| 0,3 | 0,24 | 0,3 | 0,26 |
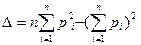
Δ=6 [2(0,1)2 +2(0,2)2 +2(0,3)2 ] – (0,6+0,6)2 = 6 • 0,28 – 1,44=0,24
tgφн = (1/0,24) • 6 ( 0,014 + 0,036 + 0,072 + 0,016 + 0,038 + 0,078 )- 1,2 • 1,17 =0,5
cн = (1/0,24) • (1,17 • 0,28 – 1,2 • 0,254 = 0,024/0.24 = 0,10 МПа
Среднеквадратичные отклонения:
στ = 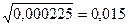 ; σс = 0,015 •
; σс = 0,015 • 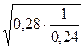 = 0,016;
= 0,016;
σtgφ = 0,015 • 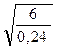 = 0,075;
= 0,075;
Коэффициент вариации:
Vc = 0,016 / 0,1 = 0,16 Vtgφ = 0,075 / 0,5 = 0,14
Показатель точности оценки среднего значения характеристики:
ρc = 1,19 • 0,16 = 0,19 ρtgφ = 1,19 • 0,14 = 0,167
Коэффициенты надежности по грунту:
γgc = 1/ ( 1-0,19) = 1,24 γgφ = 1/ ( 1-0,167) = 1,20
Тогда расчетные характеристики будут:
С = 0,10 / 1,24 = 0,08 МПа; tgφ = 0,500 / 1,20 = 0,42
В настоящее время составлены таблицы:
· нормативных значений удельного сцепления С , угла внутреннего трения φ, модуля общей деформации Е песчаных грунтов четвертичных отложений (таблица 10.2);
· нормативных значений удельного сцепления С , угла внутреннего трения φ пылевато-глинистых грунтов четвертичных отложений (таблица 10.3);
· нормативных значений модуля общей деформации Е пылевато-глинистых нелессовых грунтов (таблица 10.4).
Табличные нормативные значения прочностных и деформационных характеристик применяют для предварительных расчетов оснований, а также для окончательных расчетов оснований зданий и сооружений 2 и 3 классов и опор воздушных линий электропередач.
Расчетные значения характеристик в этом случае определяют при следующих значениях коэффициента надежности по грунту:
· в расчетах оснований по деформациям γg =1,
· по несущей способности
для удельного сцепления γgc= 1,5,
угла внутреннего трения песчаных грунтов γgφ = 1,1,
угла внутреннего трения пылевато-глинистых грунтов γgφ = 1,15.
Таблица 10.2.
Нормативные значения удельного сцепления сн, угла внутреннего трения jн и модуля общей деформации Е песчаных грунтов четвертичных отложений
| Песчаные грунты | Обозначение характеристик грунтов | Характеристики грунтов при коэффициенте пористости e, равном | |||
| 0,45 | 0,55 | 0,65 | 0,75 | ||
| Гравелистые и крупные | с, МПа | 0,002 | 0,001 | ||
| jн , град | — | ||||
| Е,МПа | — | ||||
| Средней крупности | с, МПа | 0,003 | 0,002 | 0,001 | — |
| jн , град | — | ||||
| Е, МПа | |||||
| Мелкие | с, МПа | 0,006 | 0,004 | 0,002 | — |
| jн , град | |||||
| Е ,МПа | |||||
| Пылеватые | с, МПа | 0,008 | 0,006 | 0,004 | 0,002 ,' |
| jн , град | |||||
| Е , МПа |
Таблица 10.3.
Нормативные значения удельного сцепления сн,
угла внутреннего трения jн четвертичных пылевато-глинистых грунтов
| Наименование грунтов и пределы нормативных значений их показателя текучести | Обозначение характеристик грунтов | Характеристики грунтов при коэффициенте e, равном | |||||||
| 0.45 | 0,55 | 0,65 | 0,75 | 0.85 | 0,95 | 1,05 | |||
| Супеси | 0 £ IL £ 0,25 | сн , Мпа ", град | 0,021 | 0,017 | 0,015 | 0,013 | — | — | — |
| jн , град | — | — | — | ||||||
| 0,25 £ IL £ 0,75 | сн , Мпа | 0.019 | 0,015 | 0,013 | 0,011 | 0,09 | — | — | |
| jн , град | — | — | |||||||
| Суглинки | 0£ IL £ 0,25 | сн , Мпа | 0,047 | 0,037 | 0,031 | 0,025 | 0,022 | 0,019 | — |
| jн , град | — | ||||||||
| 0,25 £ IL £ 0,5 | сн , Мпа | 0,039 | 0,034 | 0,028 | 0,023 | 0.018 | 0,015 | — | |
| jн , град | — | ||||||||
| 0,5 £ IL £ 0,75 | сн , Мпа | — | — | 0,025 | 0,020 | 0,016 | 0,014 | 0,012 | |
| jн , град | — | — | |||||||
| Глины | 0 £ IL £ 0,25 | сн , Мпа | — | 0,081 | 0,068 | 0,054 | 0,047 | 0,041 | 0,036 |
| jн , град | — | ||||||||
| 0,25 £ IL £ 0,5 | сн , Мпа | — | — | 0,057 | 0,050 | 0,043 | 0,037 | 0,032 | |
| jн , град | — | — | |||||||
| 0,50 £ IL £ 0,75 | сн , Мпа | — | — | 0,045 | 0,041 | 0,036 | 0,033 | 0,029 | |
| jн , град | — | — |
| Происхождение и возраст грунтов | Наименование грунтов и пределы нормативных значении их показателя текучести | Модуль деформации Е (МПа) при коэффициенте пористости e, равном | |||||||||||
| 0.35 | 0,45 | 0,55 | 0,65 | 0,75 | 0,85 | 0,95 | 1,05 | 1,2 | 1,4 | 1,6 | |||
| Аллювиальные | Супеси | 0£ IL £ 0,75 | — | — | — | — | — | — | |||||
| Делювиальные | Суглинки | 0£ IL £ 0,25 | — | — | — | — | — | ||||||
| Озерные | 0,25£ IL £ 0.5 | — | — | — | — | — | |||||||
| Озерно-аллювиальные | 0,5 £ IL £ 0,75 | — | — | — | — | — | — | ||||||
| 0 £ IL £ 0,25 | — | — | — | — | — | ||||||||
| Глины | 0,25£ IL £ 0,5 | — | — | — | — | — | — | ||||||
| 0,5 £ IL £ 0,75 | — | — | — | — | — | — | — | ||||||
| Флювиогляциаль- ные | Супеси | 0£ IL £ 0,75 | — | — | — | — | — | — | |||||
| 0£ IL £ 0,25 | — | — | — | — | — | — | — | ||||||
| Суглинки | 0,25 £ IL £ 0,5 | — | — | — | — | — | — | ||||||
| 0,5 £ IL £ 0,75 | — | — | — | — | — | — | — | ||||||
| Моренные | Супеси | IL £ 0,5 | — | — | — | — | — | — | — | — | |||
| Юрские отложения | Глины | 0,25£ IL £ 0 | — | — | — | — | — | — | — | — | |||
| яруса | 0 £ IL £ 0.25 | — | — | — | — | — | — | — | |||||
| 0,25 £ IL £ 0,5 | — | — | — | — | — | — | — | — | |||||
Таблица 10.4
Нормативные значения модуля общей деформации пылевато-глинистых нелессовых грунтов
11. ОПРЕДЕЛЕНИЕ НАПРЯЖЕННОГО СОСТОЯНИЯ В ГРУНТОВОМ МАССИВЕ НА ОСНОВЕ ТЕОРИИ ЛИНЕЙНО ДЕФОРМИРУЕМЫХ ТЕЛ
Расчет напряжений необходимдля установления условий прочности и устойчивости грунтов и определения их деформаций под действием внешних сил и собственного веса грунта. Задача решается на основе теории линейно деформируемых тел (линейная зависимость между деформациями и напряжениями), что справедливо для массива грунта при отсутствии в нем областей предельного напряженного состояния, предшествующего разрушению, и для грунта в конечном (стабилизированном) состоянии.
11.1. Распределение напряжений в случае пространственной задачи.
11.1.1. Действие сосредоточенной силы (основная задача Буссинеска).
Рассмотрим действие сосредоточенной силы Р,приложенной к плоскости, ограничивающей полупространство.
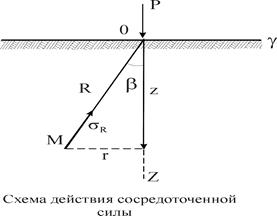
Принимается, как постулат, что величина нормального напряжения sRв точке Мс полярными координатами (R,b),направленного по радиусу-вектору,
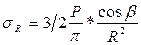 .
.
Для плоскости, параллельной плоскости приложения нагрузки, напряжение
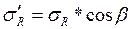 , причем,
, причем, 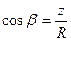 .
.
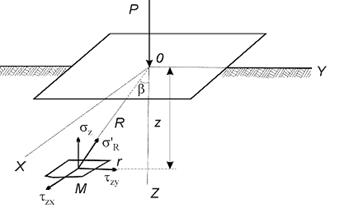
Рис. 11.1 Составляющие напряжений для площадки, параллельной плоскости приложения нагрузки.
тогда 
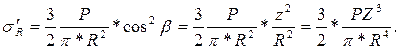

Определим нормальное напряжение sz :
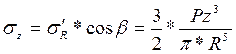 ,
,
но 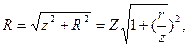 следовательно,
следовательно,
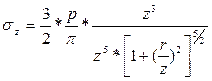 ;
;
обозначим 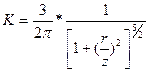 =
= 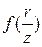 ,
,
тогда вертикальное сжимающее напряжение в массиве грунта для плоскостей, параллельных плоскости приложения нагрузки
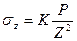 .
.
Эта формула лежитв основе всех расчетов по деформациям, коэффициент К определяется по таблицам в зависимости от параметров z и r,
где r - расстояние по горизонтали, z – глубина по вертикали от точки приложения нагрузки до точки М в массиве грунта.
Для нескольких сосредоточенных сил, приложенных к поверхности в разных точках, вертикальное сжимающее напряжение в любой точке массива для горизонтальных площадок, параллельных ограничивающей плоскости, определяется простым суммированием. Таким образом, напряжение в точке М, расположенной на глубине z на расстояниях ri от точек приложения нагрузки определяется по формуле:
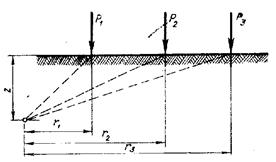
Рис. 11. 2 Схема расчета внутренних напряжений для нескольких точек приложения внешней нагрузки
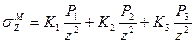
где коэффициенты Ki определятся по таблице в зависимости от соотношений ri.
Таблица 11.1
Значение коэффициента К для вычисления сжимающих напряжений от действия сосредоточенной силы в зависимости от соотношения r / z.
| r / z | К | r / z | К | r / z | К | r / z | К |
| 0,00 | 0,4775 | 0,50 | 0,2733 | 1,00 | 0,0844 | 1,50 | 0,0251 |
| 0,01 | 0,4773 | 0,51 | 0,2679 | 1,01 | 0,0823 | 1,51 | 0,0245 |
| 0,02 | 0,4770 | 0,52 | 0,2625 | 1,02 | 0,0803 | 1,52 | 0,0240 |
| 0,03 | 0,4764 | 0,53 | 0,2571 | 1,03 | 0,0783 | 1,53 | 0,0234 |
| 0,04 | 0,4756 | 0,54 | 0,2518 | 1,04 | 0,0764 | 1,54 | 0,0229 |
| 0,05 | 0,4745 | 0,55 | 0,2466 | 1,05 | 0,0744 | 1,55 | 0,0224 |
| 0,06 | 0,4732 | 0,56 | 0,2414 | 1,06 | 0,0727 | 1,56 | 0,0219 |
| 0,07 | 0,4717 | 0,57 | 0,2363 | 1,07 | 0,0709 | 1,57 | 0,0214 |
| 0,08 | 0,4699 | 0,58 | 0,2313 | 1,08 | 0,0691 | 1,58 | 0,0209 |
| 0,09 | 0,4679 | 0,59 | 0,2263 | 1,09 | 0,0674 | 1,59 | 0,0204 |
| 0,10 | 0,4657 | 0,60 | 0,2214 | 1,10 | 0,0658 | 1,60 | 0,0200 |
| 0,11 | 0,4663 | 0,61 | 0,2165 | 1,11 | 0,0641 | 1,61 | 0,0195 |
| 0,12 | 0,4607 | 0,62 | 0,2117 | 1,12 | 0,0626 | 1,62 | 0,0191 |
| 0,13 | 0,4579 | 0,63 | 0,2070 | 1,13 | 0,0610 | 1,63 | 0,0187 |
| 0,14 | 0,4548 | 0,64 | 0,2024 | 1,14 | 0,0595 | 1,64 | 0,0183 |
| 0,15 | 0,4516 | 0,65 | 0,1978 | 1,15 | 0,0581 | 1,65 | 0,0179 |
| 0,16 < |
Дата добавления: 2021-12-14; просмотров: 531;











