Физический маятник. Математический маятник
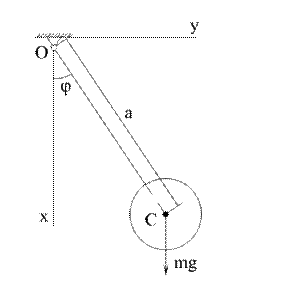 Рис. 4.3
Рис. 4.3
|
Физическим маятником называется твердое тело, которое может совершать колебания вокруг неподвижной горизонтальной оси в поле сил тяжести (рис. 4.3). Проведем через центр масс тела С плоскость, перпендикулярную оси вращения. Точка пересечения О этой плоскости с осью вращения называется точкой подвеса. Примем эту точку за начало координат. Оси х и у расположим в плоскости, проходящей через центр масс и точку подвеса, ось z направим по оси вращения (перпендикулярно плоскости xoy).
Дифференциальный закон вращения тела вокруг оси z, согласно (4.4), запишется
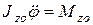 . (4.5)
. (4.5)
Здесь 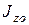 - момент инерции тела, относительно оси, проходящей через точку подвеса;
- момент инерции тела, относительно оси, проходящей через точку подвеса; 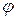 - угол между неподвижной осью х и линией ОС (рис.4.3).
- угол между неподвижной осью х и линией ОС (рис.4.3).
Так как в этом случае
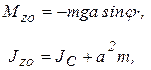 (
( 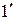 )
)
здеь m – масса тела; а – расстояние от точки О до центра масс (а 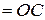 );
); 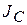 - момент инерции тела относительно оси
- момент инерции тела относительно оси 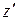 , проходящей через центр масс С.
, проходящей через центр масс С.
Дифференциальное уравнение вращательного движения тела (4.5) c учетом ( 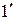 ) примет вид
) примет вид
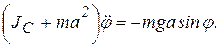 (4.5а)
(4.5а)
Знак минус в уравнении означает, что момент силы тяжести направлен против увеличения угла 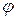 . Если угол отклонения мал, то с большой точностью можно считать
. Если угол отклонения мал, то с большой точностью можно считать 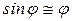 , тогда уравнение (4.5а) перепишется в виде
, тогда уравнение (4.5а) перепишется в виде
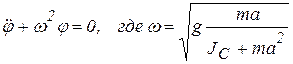 . (4.6)
. (4.6)
Полученное уравнение совпадает по форме с дифференциальным уравнением свободных колебаний точки и его общим решением будет
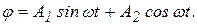
Полагая, что в начальный момент t=0 маятник отклонен на малый угол 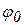 и отпущен без начальной скорости (
и отпущен без начальной скорости ( 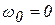 ), найдем для постоянных интегрирования значения А1=0,А2=
), найдем для постоянных интегрирования значения А1=0,А2= 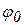 , тогда
, тогда
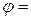
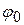
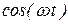 .
.
Маятник совершает колебания с малой амплитудой 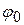 , частота и период которых определяются формулами
, частота и период которых определяются формулами
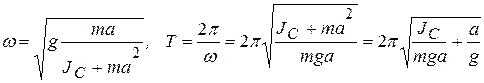 . (4.7)
. (4.7)
Такие колебания называются гармоническими, а уравнение (4.6) называется уравнением гармонических колебаний.
Пусть физический маятник состоит из материальной точки массой m, подвешенной на невесомой нити длиной а и колеблющейся около точки подвеса О. Такой маятник называется математическим. Поскольку момент инерции материальной точки относительно оси z, проходящей через центр С равен нулю, т.е. 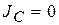 , из (4.7) находим частоту и период колебаний математического маятника:
, из (4.7) находим частоту и период колебаний математического маятника:
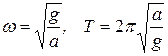 . (4.8)
. (4.8)
Сравнение формул (4.7) и (4.8) показывает, что период колебаний математического маятника меньше периода колебаний физического маятника той же длины.
Дата добавления: 2019-12-09; просмотров: 331;










