Вокруг неподвижной оси
Твердое тело, вращающееся вокруг неподвижной оси, является примером несвободного твердого тела. Следовательно, при изучении его движения необходимо (применив аксиому связей) отбросить связи и, заменив их реакциями связей, рассматривать твердое тело как свободное.
Рассмотрим вращение тела относительно неподвижной оси z, проходящей через центр масс (рис. 4.2). Тогда положение тела будет определяться углом 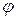 между плоскостями zСх и
между плоскостями zСх и 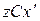 (оси x,y – неподвижны; оси
(оси x,y – неподвижны; оси 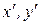 - связаны с телом и вращаются вместе с ним). Для нахождения закона, описывающего вращение тела вокруг неподвижной оси, воспользуемся законом движения свободного тела в плоскости (4.1). Поскольку
- связаны с телом и вращаются вместе с ним). Для нахождения закона, описывающего вращение тела вокруг неподвижной оси, воспользуемся законом движения свободного тела в плоскости (4.1). Поскольку 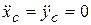 , имеем
, имеем
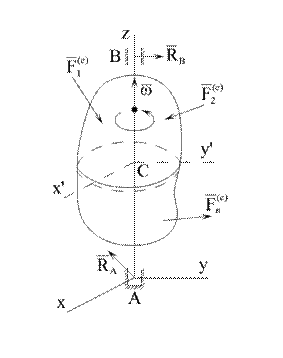 Рис. 4.2
Рис. 4.2
|
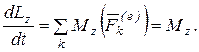 (4.3)
(4.3)
Здесь 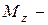 главный момент внешних сил.
главный момент внешних сил.
При вращении твердого тела вокруг неподвижной оси, согласно (3.16), кинетический момент
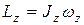 ,
,
где 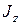 - постоянный для твердого тела момент инерции относительно оси вращения;
- постоянный для твердого тела момент инерции относительно оси вращения; 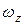 - угловая скорость вращения. Учитывая это, получаем из (4.3)
- угловая скорость вращения. Учитывая это, получаем из (4.3)
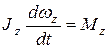 . (4.3а).
. (4.3а).
Известно, что 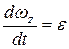 , тогда
, тогда
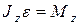 . (4.4)
. (4.4)
Это и есть дифференциальный закон вращения твердого тела вокруг неподвижной оси z. Реакции подшипников 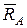 и
и 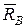 считаем внешними силами (отметим, что они не создают моменты относительно оси вращения, т.к. линии их действия пересекают эту ось).
считаем внешними силами (отметим, что они не создают моменты относительно оси вращения, т.к. линии их действия пересекают эту ось).
В частном случае, когда
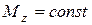 , то
, то 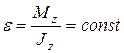 ,
,
т.е. вращение тела происходит с постоянным угловым ускорением. Такое вращение называется равнопеременным вращением.
Если
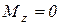 , то
, то 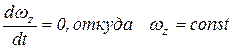 .
.
Это случай равномерного вращения тела, т.е. вращения тела по инерции.
Дифференциальное уравнение (4.4) в общем случае позволяет решить две основные задачи динамики:
· первая задача связана с дифференцированием: по заданному уравнению вращения тела 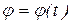 определяют
определяют 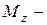 главный момент внешних сил.
главный момент внешних сил.
· вторая задача связана с интегрированием уравнения (4.4): по заданному главному моменту внешних сил 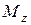 и начальным условиям задачи, находят уравнение вращения тела
и начальным условиям задачи, находят уравнение вращения тела 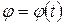 .
.
Дата добавления: 2019-12-09; просмотров: 749;











