Сила. Второй и третий законы Ньютона

При взаимодействии материальной точки с внешними телами ее импульс со временем изменяется. За меру изменения импульса принимается величина 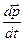, называемая силой. Сила есть мера механического воздействия на материальную точку (или материальное тело) со стороны других тел или полей, в результате чего точка (тело) получает ускорение или изменяет свою форму и размеры.

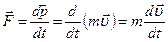, (2.6)

следовательно

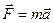(2.7)

Сила, действующая на материальную точку, равна произведению массы этой точки на ускорение, которое вызвано действием этой силы. Это утверждение носит название II закона Ньютона.

Сила вызывает изменение скорости или деформацию. В окружающем нас мире действуют силы различной природы. Изучая механику, мы будем рассматривать три вида сил: силы трения, силы упругости и силы тяготения. Более подробно речь об этих силах пойдет чуть позже. Пространство, где действуют силы, называется силовым полем.

Большое значение в механике имеет принцип независимости действия сил: если на материальную точку воздействует одновременно несколько сил 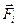, то каждая из них сообщает этой материальной точке ускорение 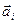согласно II закону Ньютона, как будто другие силы не действуют. Результирующее ускорение определяется как векторная сумма ускорений, полученных в результате действия каждой отдельно взятой из приложенных к точке сил 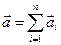. Другими словами, результирующее ускорение вызывается действием результирующей силы, определяемой как векторная сумма отдельных сил, действующих на эту точку .

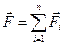II закон Ньютона иначе называют основным законом динамики поступательного движения. Он объединяет I и III законы.

Из уравнения 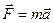видно, что если 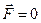, то 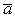= 0. Это и есть I закон Ньютона.

Рассмотрим, как получается III закон Ньютона.

По закону сохранения импульса (см. 2.2)

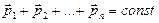
Продифференцировав это уравнение по времени t, получим

,

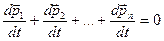следовательно

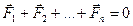(2.8)

Для двух тел

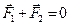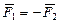или (2.9)

Выражение (2.9) и представляет собой III закон Ньютона: всякое действие тел друг на друга носит характер взаимодействия – силы, с которыми взаимодействуют материальные точки, равны по величине, противоположны по направлению и действуют вдоль прямой, соединяющей эти точки.

Сила трения

При движении тела по горизонтальной поверхности на него действует сила, препятствующая движению – сила трения, то есть сила сопротивления, направленная в сторону противоположную перемещению.

Различают трение внутреннее (жидкое или вязкое) и внешнее.

Внутренним трением называется трение, возникающее между частями одного и того же тела, например, между слоями жидкости или газа, скорости которых меняются от слоя к слою. Пусть между плоскостями I и II вязкая среда. Если плоскость I движется относительно плоскости II со скоростью u (рис. 2.1), то

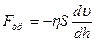(2.10)

где F_тр – тангенциальная (касательная) сила, вызывающая сдвиг слоев вязкой среды друг относительно друга,

S – площадь плоскости I,

h – коэффициент динамической вязкости или вязкость,

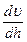– градиент скорости – быстрота изменения скорости от слоя к слою, т.е. в направлении, перпендикулярном движению, иначе – скорость сдвига.

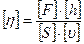= Па·с (2.11)

Внешнее трение возникает в плоскости соприкосновения двух тел (рис. 2.2).

Если соприкасающиеся тела неподвижны, то в момент начала движения возникающее между телами трение называется трением покоя. Сила трения покоя – это максимальная сила, необходимая, чтобы привести в движение одно тело относительно другого.

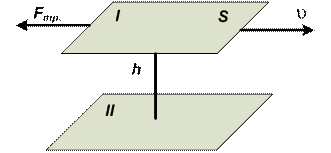
Рис. 2.1

F_тр = μ₀ N (2.12)

где μ₀ – коэффициент трения покоя, N – сила нормального давления.

При движении одного тела по поверхности другого возникает трение скольжения.

F_тр = μ N (2.13)

μ – коэффициент трения скольжения

μ < μ₀, то есть сила трения покоя больше силы трения скольжения.

Для определения коэффициента трения используется наклонная плоскость (рис. 2.3). Угол наклонной плоскости увеличивают до тех пор, пока тело не начнет скатываться по плоскости. В этом случае сила трения 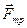будет равна сказывающей силе :

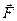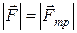, т.е. ,

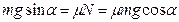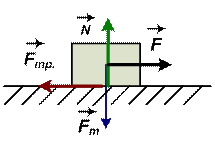
Рис. 2.2.

откуда

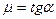(2.14)

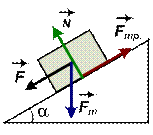
Рис. 2.3

Одним из видов внешнего трения является трение качения, которое проявляется, когда тело катится по опоре (рис.2.4). Оно значительно меньше трения скольжения m_k << m.

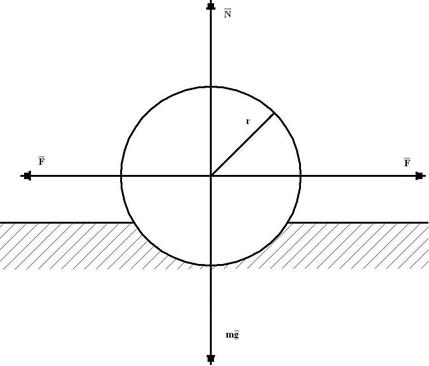
Рис. 2.4

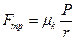(2.15)

где P – вес катка, r – радиус, μ_k – коэффициент трения качения.

Из (2.15) видно, что сила трения качения обратно пропорциональна радиусу катящегося тела.

Трение играет большую роль в природе и технике. В некоторых случаях трение играет положительную роль и его стремятся увеличить (например, изготовление автомобильных шин со специальным рисунком протектора, увеличивающим трение между колесами и поверхностью дорожного покрытия, посыпание песком дорог во время гололеда). Но иногда приходится бороться с негативными проявлениями, вызываемыми трением с помощью смазок. В данном случае используется тот факт, что внутреннее трение, возникающее между слоями жидкости значительно меньше внешнего трения, возникающего между частями твердых тел. Другой способ уменьшить внешнее трение – заменить трение скольжения трением качения, применяя шариковые и роликовые подшипники и т.д.

Сила упругости

Как уже было отмечено выше, сила вызывает либо ускорение, либо деформацию тела. Деформация – это всякое изменение размеров или формы тела под действием внешних сил. Если после прекращения действия сил деформация исчезает, она называется упругой. Если же после прекращения действия сил деформация сохраняется, она называется пластической.

Различают следующие виды деформации: всесторонние растяжение или сжатие, сдвиг, кручение.

Рассмотрим однородный стержень длиной 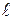, диаметром d и площадью поперечного сечения S, к концу которого приложена сила F (рис.2.5). Под действием силы F длина стержня увеличивается на величину 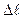, а диаметр уменьшается на ∆d. Сила, действующая на единицу площади поперечного сечения, называется напряжением и обозначается s.

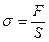(2.17)

Количественной мерой деформации является относительная деформация. При продольном растяжении (сжатии) относительная продольная деформация

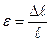(2.18)

где 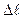– абсолютная деформация (изменение длины);

При продольном растяжении (сжатии) происходит поперечное сжатие (растяжение)

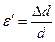(2.19)

где 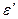– относительная поперечная деформация;

∆d – абсолютная деформация (изменение диаметра);

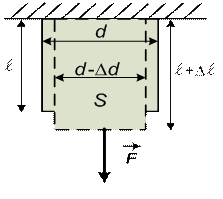
Рис. 2.5

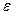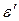, – имеют разные знаки, так как при растяжении длина стержня увеличивается ( 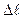>0), а диаметр уменьшается (∆d<0) и наоборот при сжатии.

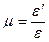(2.20)

где 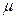– коэффициент Пуассона[1].

Английский ученый Р.Гук[2] экспериментально установил, что для малых деформаций напряжение 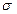прямо пропорционально относительному удлинению .

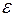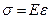(2.21)

где Е – модуль Юнга[3].

Если 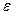=1 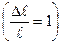, то Е = .

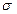Другими словами, модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице (т.е. ).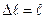

Модуль Юнга – теоретическая величина, так как нет материала (кроме резины) который мог бы удлиняться в 2 раза без разрыва.

Подставляя в формулу (2.21) 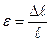и 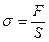получим

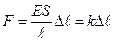(2.22)

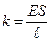– коэффициент упругости.

Закон Гука приобретает вид

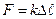(2.23)

Деформация подчиняется закону Гука до известного предела.

Из рис.2.6 видно, что линейная зависимость 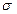( 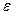) соответствует участку оa (деформация на этом участке – упругая); участок ab соответствует пластической деформации, а od – остаточной деформации. Значение 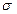при котором тело разрушается – называется пределом прочности. Если предел упругости совпадает с пределом прочности тело называется хрупким.

Сила тяготения

Ньютон, изучая движения планет на основании законов Кеплера[4] и законов динамики, установил закон всемирного тяготения. Этот закон сначала был сформулирован для планет, которые рассматривались как материальные точки по сравнению с расстоянием между ними и в дальнейшем обобщен на любые тела. Закон всемирного тяготения формулируется следующим образом: две материальные точки притягиваются друг к другу с силой прямо пропорциональной произведению масс этих точек и обратно пропорциональной квадрату расстояния между ними.

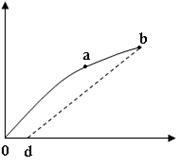
Рис. 2.6

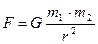(2.24)

где F – сила всемирного тяготения (или гравитационная сила); m₁ и m₂ массы материальных точек; r – расстояние между ними.

Коэффициент пропорциональности G – гравитационная постоянная, которая определяется опытным путем и равна 6,6745·10^‑11 м³/кг·с². Так, два точечных тела массой 1 кг, находящиеся на расстоянии 1 м, притягиваются друг к другу с силой 6,6745 · 10^-11 Н.

В векторном виде закон всемирного тяготения выглядит следующим образом

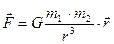(2.25)

Согласно этому закону, на любое тело массой m, находящееся вблизи Земли действует сила тяготения, которая по II закону Ньютона придает ему ускорение свободного падения g:

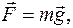(2.26)

где 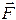- называется силой тяжести.

Если пренебречь вращением Земли, для тела находящегося на земной поверхности

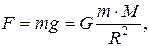(2.27)

а в векторной форме

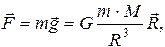(2.28)

где M - масса Земли, R - радиус Земли

Из формулы (2.27) видно, что

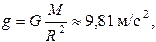(2.29)

Если тело находится на высоте h (r=R+h) то

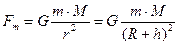(2.30)

В результате действия силы тяготения (а также действия других сил) тело действует на опору или подвес с силой, которая называется вес тела и обозначается 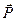. Следует различать вес тела и силу тяжести. Вес тела проявляется в случае, когда тело движется с ускорением, имеющим вертикальную составляющую. В общем случае вес тела может быть вычислен по формуле

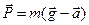(2.31)

Если вертикальная составляющая ускорения направлена вниз (сонаправлена вектору ускорения свободного падения), вес тела уменьшается и в предельном случае, когда a=g вес тела становится равным нулю и наступает состояние невесомости.

Если вертикальная составляющая ускорения направлена вверх (противоположно вектору ускорения свободного падения), вес тела увеличивается и тело испытывает перегрузки.

Гравитационное взаимодействие осуществляется через поле тяготения (или гравитационное поле). Силовой характеристикой поля является напряженность Е.

Напряженность поля Е число равна отношению силы тяготения F к массе тела m.

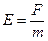(2.32)

Согласно II закону Ньютона 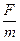равно ускорению a. Тогда для поля тяготения

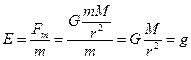(2.33)

Напряженность гравитационного поля 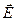– векторная величина и направлена в ту же сторону, что и сила тяготения .

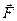Ускорение g как и напряженность Е не зависят от массы тела, поэтому, все тела падают в поле силы тяжести с одинаковым ускорением g.

[1] Симеон Дени Пуассон (Simeon-Denis Poisson) (1781–1840), французский математик, механик и физик.

[2] РобертГук (Robert Hooke) (1635–1703), английский естествоиспытатель.

[3] ТомасЮнг (Thomas Young) (1773–1829), английский физик.

[4] ИоганнКеплер (Johann Kepler) (1571–1630), немецкий астроном.