Теорема Гюйгенса-Штейнера
Существует простая связь между моментами инерции тела относительно параллельных осей (теорема Гюйгенса-Штейнера), одна из которых проходит через центр масс.
Теорема. Момент инерции тела 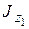 относительно некоторой оси
относительно некоторой оси 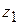 равен сумме момента инерции
равен сумме момента инерции 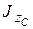 тела относительно оси
тела относительно оси 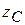 , проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояний между осями:
, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояний между осями:
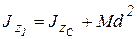 , (2.13)
, (2.13)
где М – масса тела, d – расстояние между двумя параллельными осями.
 Пусть оси
Пусть оси 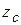 и
и 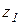 параллельны, причем ось
параллельны, причем ось 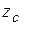 проходит через точку С – центр масс тела.
проходит через точку С – центр масс тела.
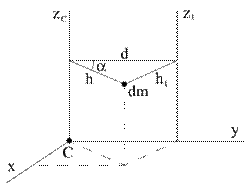
Возьмем начало координат в точке С, совместим ось zс осью 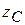 , а ось у направим так, чтобы она пересекала оси
, а ось у направим так, чтобы она пересекала оси 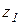 и
и 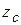 (рис. 2.5).
(рис. 2.5).
Рис.2.5 Выделим в теле произвольный элемент массой dm и опустим из него перпендикуляры на оси z и 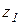 , обозначив их соответственно h и
, обозначив их соответственно h и 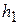 . Согласно определению осевых моментов инерции моментов (2.7), будем иметь
. Согласно определению осевых моментов инерции моментов (2.7), будем иметь
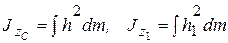 .
.
По теореме косинусов (рис.2.5) найдем 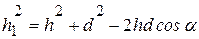 , однако
, однако 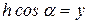 , где у – координата элемента, тогда
, где у – координата элемента, тогда
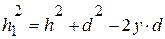 .
.
Подставим полученное выражение 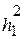 в формулу (2.13), определяющую момент инерции
в формулу (2.13), определяющую момент инерции 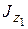 :
:
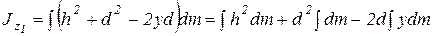 .
.
Первый интеграл равен 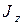 по определению, второй – массе тела М, а третий – нулю:
по определению, второй – массе тела М, а третий – нулю: 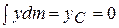 , поскольку начало координат совпадает с центром масс. Следовательно,
, поскольку начало координат совпадает с центром масс. Следовательно,
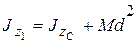 .
.
Эта формула широко используется в практических расчетах при определении моментов инерции тел относительно осей, не проходящих через центр масс. Применяя метод разбиения, с помощью этой формулы можно определять осевые моменты инерции тел сложной формы.
Установим формулы для центробежных моментов инерции, аналогичные (2.13). Рассмотрим две системы координат с взаимно параллельными осями 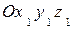 и Сxyz, где С-центр масс тела (рис. 2.6). Обозначим через a,b,c координаты точки С в системе
и Сxyz, где С-центр масс тела (рис. 2.6). Обозначим через a,b,c координаты точки С в системе 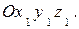 Тогда формулы перехода от одной системы координат к другой будут иметь вид
Тогда формулы перехода от одной системы координат к другой будут иметь вид
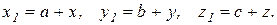
 Рис. 2.6
Рис. 2.6
По определению центробежных моментов инерции имеем
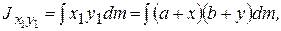
или, раскрывая скобки, группируя члены и вынося постоянные множители за знак интеграла,
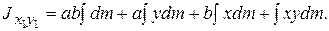
Первый интеграл равен массе тела М, второй и третий равны нулю (они соответственно определяют положение центров тяжести 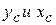 ), а последний равен
), а последний равен 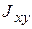 по определению. Таким образом, имеем (две другие формулы получены аналогично)
по определению. Таким образом, имеем (две другие формулы получены аналогично)
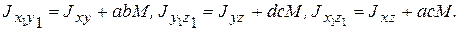 (2.14)
(2.14)
Дата добавления: 2019-12-09; просмотров: 537;










