Пересечение наклонного конуса проецирующей плоскостью и построение развертки

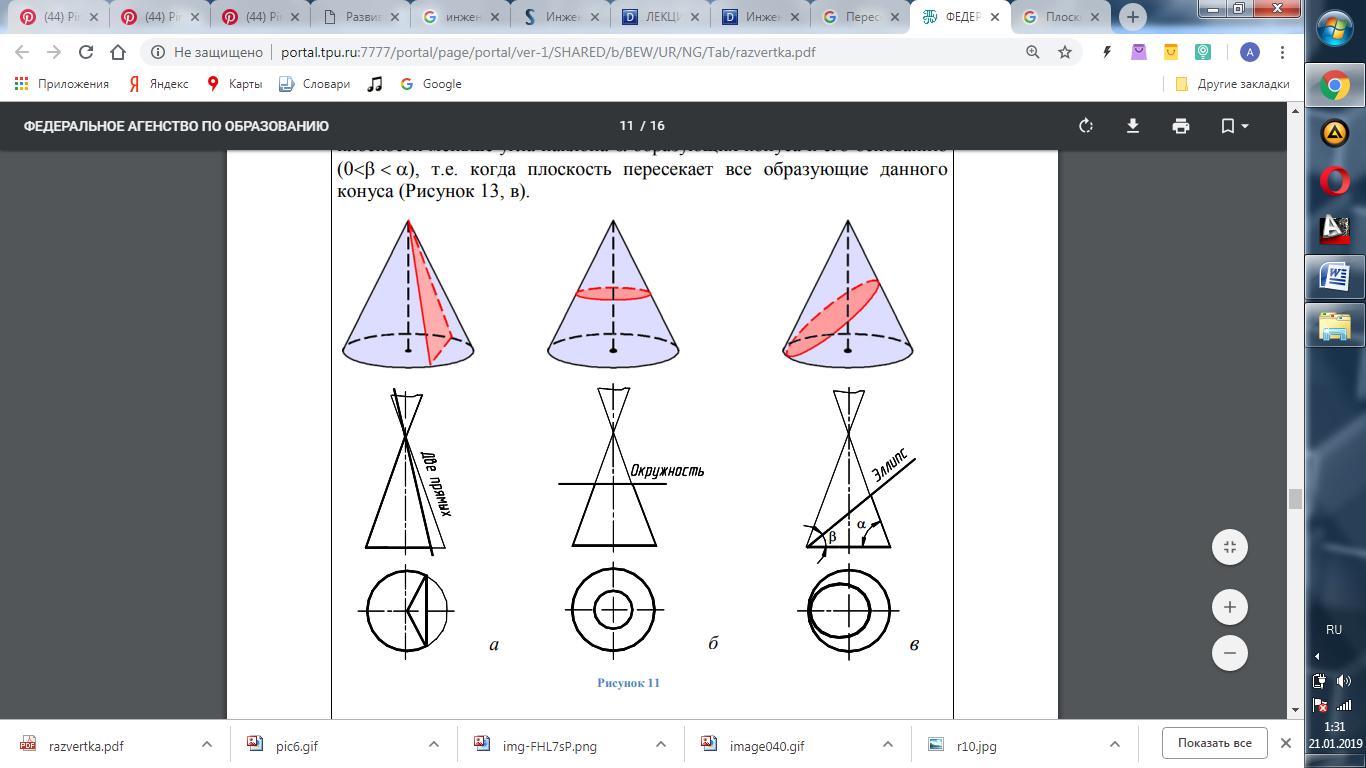В зависимости от направления секущей плоскости в сечении конуса вращения могут получиться различные типы линий.

• Если секущая плоскость проходит через вершину конуса, в его сечении получаются две прямые − образующие треугольник (Рисунок 13, а).

• В результате пересечения конуса плоскостью, перпендикулярной оси конуса, получается окружность (Рисунок 13, б).

Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении конуса может получиться эллипс (Рисунок 13, в), парабола или гипербола (Рисунок 14, а, б) – в зависимости от величины угла наклона секущей плоскости.

• Эллипс получается в том случае, когда угол β наклона секущей плоскости меньше угла наклона α образующих конуса к его основанию (0< α), т.е. когда плоскость пересекает все образующие данного конуса (Рисунок 13, в).

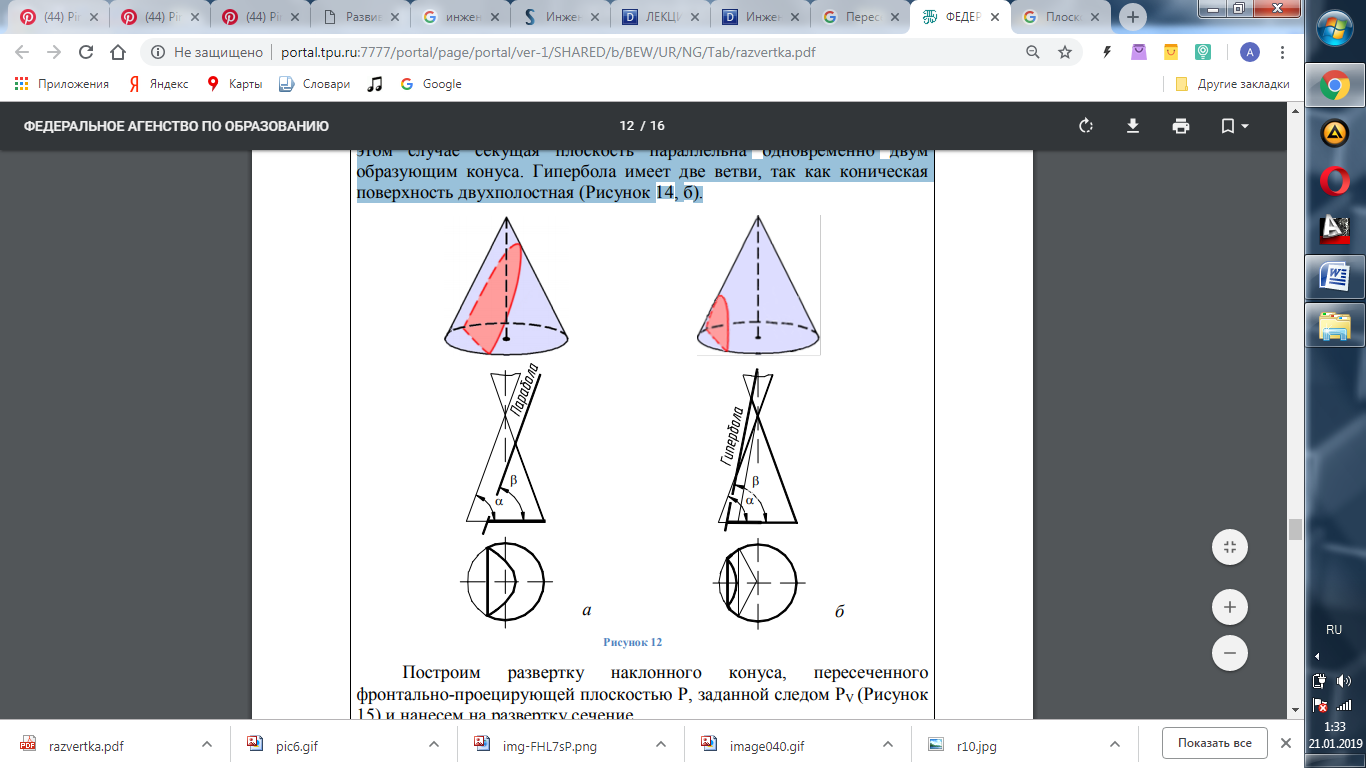· Если углы α и β равны (то есть секущая плоскость параллельна только одной из образующих конуса), в сечении получается парабола (Рисунок 14, а).

· Если секущая плоскость направлена под углом, который β/изменяется в пределах 90° > α, то в сечении получается гипербола. В этом случае секущая плоскость параллельна одновременно двум образующим конуса. Гипербола имеет две ветви, так как коническая поверхность двухполостная (Рисунок 14, б).

Тема: Комплексные чертежи 2-х пересекающихся геометрических тел

В практике часто встречаются детали машин со сложными отверстиями и вырезами, состоящие из сочетания различных геометрических тел и поверхностей.

Для выполнения комплексных чертежей таких деталей применяют метод вспомогательных секущих плоскостей (используют в том случае, если плоские поверхности отверстия располагаются параллельно основанию геометрического тела).

Для построения линии пересечения двух многогранников определяют точки пересечения ребер первого многогранника с гранями второго и ребер второго с гранями первого. Найденные точки соединяют и получают ломаную линию, отрезки которой представляют собой линии пересечения граней одного многогранника с гранями другого.

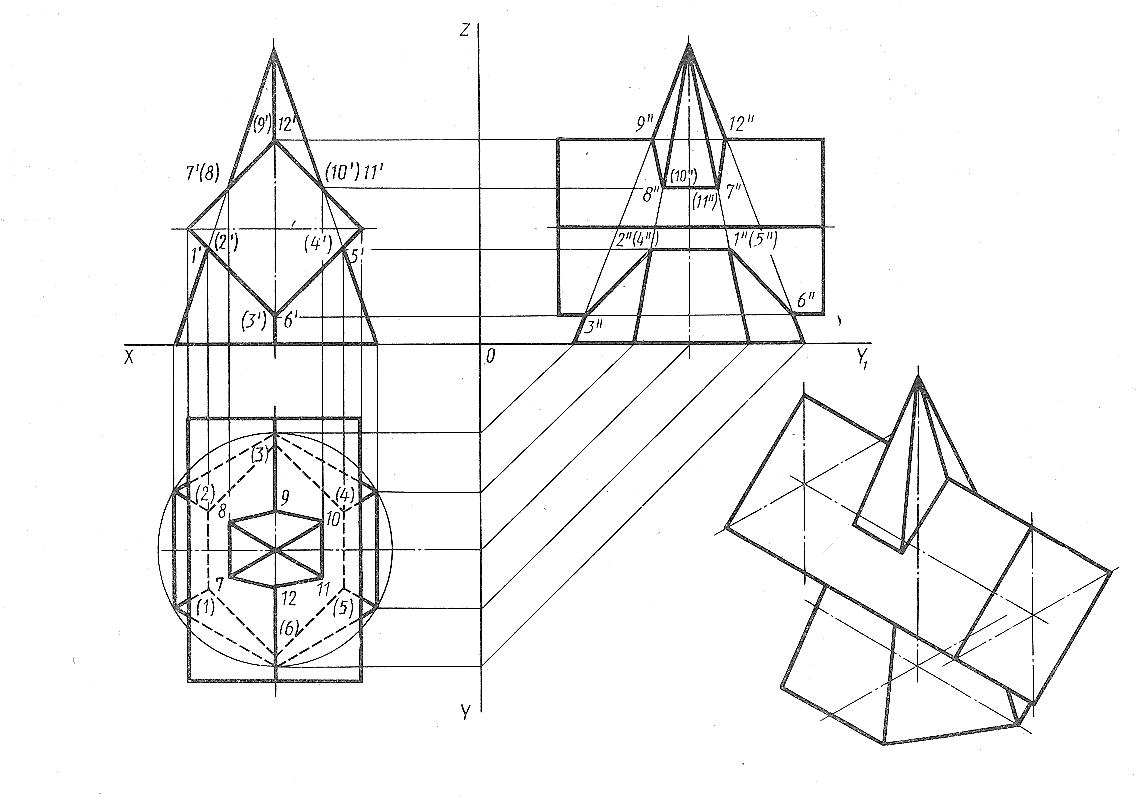
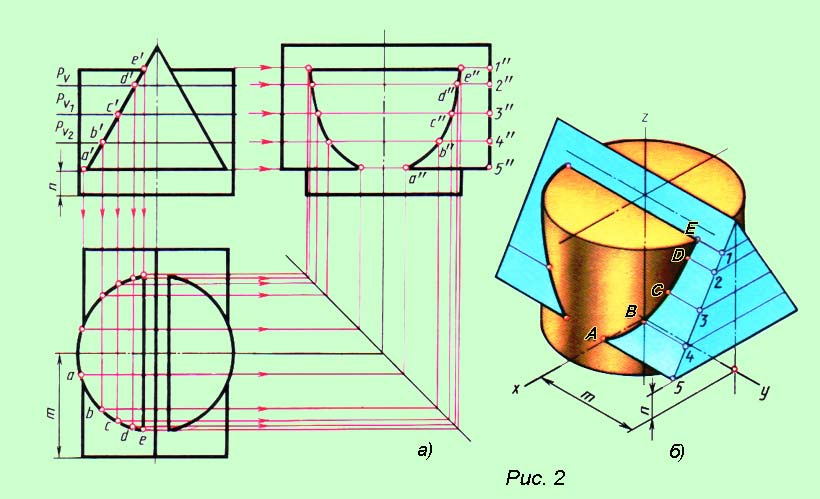
Линии пересечения поверхностей вращения обычно строят с помощью вспомогательных секущих плоскостей.

Каждая вспомогательная секущая плоскость одновременно пересекает обе заданные поверхности по соответствующим линиям (конус –по окружностям, цилиндр –по образующим). Эти линии пересекаются между собой в точках, определяющих линию пересечения заданных поверхностей.