Действия с векторами, заданными своими координатами
Рассмотрим действия с векторами, которые заданы своими координатами:
1) При сложении векторов их одноименные координаты складываются, т.е. если  , то
, то
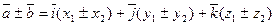 .
.
2) При умножении вектора 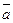 на число l необходимо умножить на это число все его координаты:
на число l необходимо умножить на это число все его координаты:
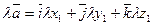
3) Рассмотрим скалярное произведение векторов, заданных своими координатами.
Пусть  , найдём их скалярное произведение
, найдём их скалярное произведение
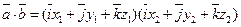 .
.
Согласно свойствам (3) и (4), имеем
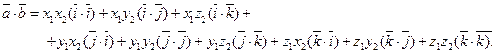
Так как 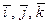 — три взаимно перпендикулярных вектора, то
— три взаимно перпендикулярных вектора, то
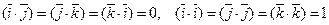
и, следовательно,
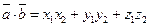 (6)
(6)
т.е. скалярное произведение равно сумме произведений одноименных координат.
Простейшие задачи аналитической геометрии (длина вектора, расстояние между двумя точками в пространстве, угол между двумя векторами, направление вектора, деление отрезка в заданном отношении)
1) Длина вектора.Применяя формулу (2.3) при 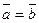 , имеем
, имеем 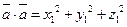 . С другой стороны
. С другой стороны 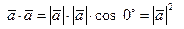 . Отсюда получаем формулу для определения длины вектора
. Отсюда получаем формулу для определения длины вектора
| 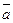 |
| 
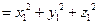 или
или 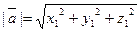 (7)
(7)
2) Расстояние между двумя точками в пространстве. Рассмотрим следующую задачу. Даны две точки M 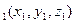 и M
и M 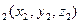 . Найти расстояние между ними.
. Найти расстояние между ними.
 Z
Z
О Y
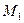
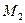
Заметим, что вектор 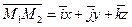 есть разность векторов
есть разность векторов
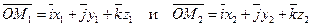 .
.
Таким образом,  . Следовательно,
. Следовательно,  . Применяя формулу (1.4), получим
. Применяя формулу (1.4), получим
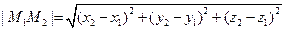 .
.
Пример 6. Определить расстояние между точками 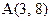 и
и 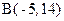 .
.
Решение. Воспользовавшись формулой (2.2), получим
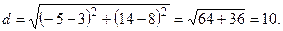
3)Угол между двумя векторами. Рассмотрим задачу об определении угла между двумя векторами. Согласно определению скалярного произведения векторов, имеем: 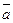 ∙
∙ 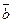 = |
= | 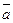 ||
|| 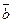 | cosj, где j — угол между векторами
| cosj, где j — угол между векторами 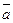 и
и 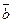 . Из этой формулы находим
. Из этой формулы находим
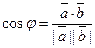 (8)
(8)
Выражая числитель и знаменатель в проекциях, получим формулу для вычисления угла между двумя данными векторами
 . (9)
. (9)
4) Направление вектора. Пусть a, b и g — углы, образованные вектором 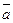 с осями координат OX, OY и OZ соответственно. Имеем
с осями координат OX, OY и OZ соответственно. Имеем 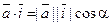 . Отсюда
. Отсюда
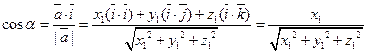 .
.
Аналогично получим
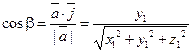 ;
; 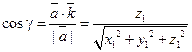 .
.
Величины cosa, cosb, cosg называются направляющими косинусами вектора 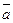 . Имеет место очевидное равенство:
. Имеет место очевидное равенство: 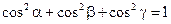 .
.
5) Деление отрезка в заданном отношении. Пусть даны точки A( 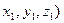 и B(
и B( 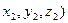 . Будем говорить, что точка M(x,y,z) делит отрезок
. Будем говорить, что точка M(x,y,z) делит отрезок 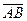 в заданном отношении l, если
в заданном отношении l, если 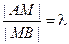 .
.
B
 M
M
 A
A

O
Требуется найти координаты точки M, делящей отрезок 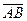 в отношении l.
в отношении l.
По условию имеем  . Обозначим через
. Обозначим через 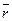 – радиус-вектор точки M,
– радиус-вектор точки M,  – радиус вектор точки A,
– радиус вектор точки A, 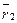 – радиус вектор точки B. Замечая, что
– радиус вектор точки B. Замечая, что 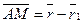 , а
, а 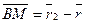 , перепишем (2.7) в виде
, перепишем (2.7) в виде 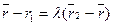 .
.
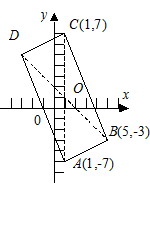 Отсюда имеем:
Отсюда имеем: 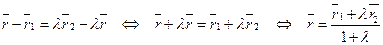
или в координатах: 
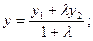
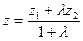 .
.
В частности координаты середины отрезка: 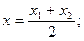
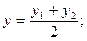
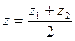 .
.
Пример 7. Даны три вершины 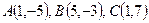 параллелограмма
параллелограмма 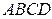 . Найти его четвертую вершину D.
. Найти его четвертую вершину D.
Решение. 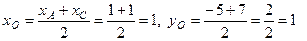
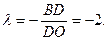

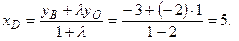
Дата добавления: 2021-11-16; просмотров: 552;











