Теоремы Больцано — Вейерштрасса и Коши
Теорема Больцано—Вейерштрасса
Как уже известно, не каждая последовательность имеет предел. Более того, не каждая ограниченная последовательность имеет предел. Однако, справедлива следующая теорема.
Теорема 2.18 (теорема Вейерштрасса). Из ограниченной последовательности точек можно извлечь сходящуюся подпоследовательность.
Доказательство.Если последовательность точек является числовой, то
эта последовательность содержит монотонную подпоследовательность (теорема 2.2). Из ограниченности последовательности следует ограниченность ее монотонной подпоследовательности, поэтому она сходится.
Докажем, что из ограниченной последовательности 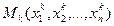 точек пространства
точек пространства 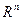 можно извлечь сходящуюся подпоследовательность.
можно извлечь сходящуюся подпоследовательность.
Первые координаты 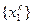 точек последовательности
точек последовательности 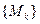 образуют ограниченную числовую последовательность. Эта последовательность содержит сходящуюся подпоследовательность
образуют ограниченную числовую последовательность. Эта последовательность содержит сходящуюся подпоследовательность 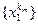 . Тогда у подпоследовательности
. Тогда у подпоследовательности 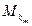 первые координаты уже имеют предел. Затем из ограниченной последовательности вторых координат
первые координаты уже имеют предел. Затем из ограниченной последовательности вторых координат  точек
точек 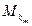 выделим сходящуюся подпоследовательность
выделим сходящуюся подпоследовательность 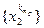 . Теперь у подпоследовательности
. Теперь у подпоследовательности 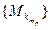 сходятся вторые координаты, а ее первые координаты
сходятся вторые координаты, а ее первые координаты 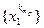 – подпоследовательность сходящейся последовательности
– подпоследовательность сходящейся последовательности 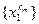 . Следовательно, у подпоследовательности
. Следовательно, у подпоследовательности 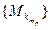 сходятся первые и вторые координаты.
сходятся первые и вторые координаты.
Через конечное число шагов получим подпоследовательность последовательности 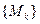 , у которой сходятся последовательности всех координат, поэтому сама подпоследовательность сходится. ■
, у которой сходятся последовательности всех координат, поэтому сама подпоследовательность сходится. ■
Критерий сходимости Коши
До сих пор мы не имеем критерия сходимости последовательности, в формулировке которого фигурировали бы только точки последовательности.
Начнем с доказательства теоремы.
Теорема 2.19.Если последовательность 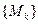 сходится, то для любого числа
сходится, то для любого числа 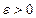 найдется такой номер
найдется такой номер 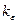 , что неравенство
, что неравенство 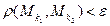 справедливо, как только
справедливо, как только 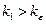 и
и 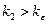 .
.
Доказательство.Пусть точка 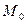 является пределом последовательности
является пределом последовательности 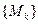 , и пусть
, и пусть 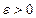 — произвольное положительное число. Тогда неравенство
— произвольное положительное число. Тогда неравенство 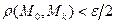 справедливо при всех
справедливо при всех 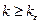 . Возьмем любые два такие номера
. Возьмем любые два такие номера 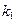 и
и 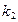 , чтобы
, чтобы 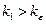 и
и 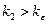 . Тогда
. Тогда 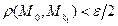 и
и 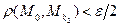 . Теперь имеем:
. Теперь имеем: 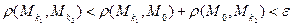 . ■
. ■
Теорема 2.19 содержит необходимое условие сходимости последовательности точек, в формулировке которого фигурируют только точки последовательности. Будет ли это условие достаточным условием сходимости последовательности точек? Ответ утвердительный, но сначала введем понятие фундаментальной последовательности точек, которое играет важную роль в современном анализе.
Последовательность точек 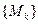 пространства
пространства 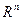 называется фундаментальной, если для любого числа
называется фундаментальной, если для любого числа 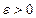 найдется такой номер
найдется такой номер 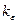 , что неравенство
, что неравенство 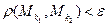 справедливо, как только
справедливо, как только 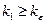 и
и 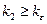 .
.
Теперь теорему 2.19 можно сформулировать так: если последовательность точек 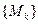 пространства
пространства 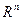 сходится, то она является фундаментальной.
сходится, то она является фундаментальной.
Лемма. Каждая фундаментальная последовательность точек 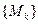 пространства
пространства 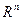 ограничена.
ограничена.
Доказательство.Если последовательность точек 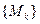 является фундаментальной, то для числа
является фундаментальной, то для числа 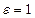 найдется такой номер
найдется такой номер 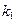 , что неравенство
, что неравенство 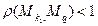 будет справедливо, как только
будет справедливо, как только 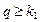 . Следовательно, все точки последовательности
. Следовательно, все точки последовательности 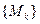 принадлежат окрестности
принадлежат окрестности  , кроме точек
, кроме точек 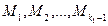 . Окрестность точки
. Окрестность точки 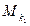 , радиус которой больше числа
, радиус которой больше числа
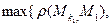
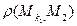 ,…,
,…, 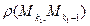 ,
, 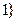 ,
,
содержит все точки последовательности 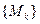 . Следовательно, множество точек последовательности
. Следовательно, множество точек последовательности 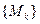 содержится в ограниченном множестве, поэтому само ограничено. ■
содержится в ограниченном множестве, поэтому само ограничено. ■
Теорема 2.20. Каждая фундаментальная последовательность точек 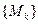 пространства
пространства 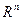 сходится.
сходится.
Доказательство. Из леммы следует, что последовательность точек 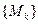 ограничена. Из теоремы 2.18 вытекает, что последовательности точек
ограничена. Из теоремы 2.18 вытекает, что последовательности точек 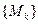 содержит подпоследовательность
содержит подпоследовательность 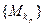 ,которая сходится к точке
,которая сходится к точке 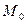 . Докажем, что эта точка является пределом последовательности
. Докажем, что эта точка является пределом последовательности 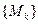 .
.
Возьмем 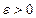 . Так как последовательность точек
. Так как последовательность точек 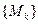 является фундаментальной, то по заданному числу
является фундаментальной, то по заданному числу 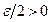 найдется такой номер
найдется такой номер 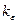 , что неравенство
, что неравенство 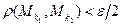 справедливо, как только
справедливо, как только 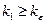 и
и 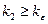 .
.
С другой стороны, точка 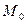 является пределом последовательности
является пределом последовательности 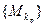 .
.
Следовательно, по заданному числу 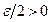 неравенство
неравенство 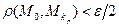 справедливо при всех
справедливо при всех 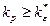 .
.
Обозначим через 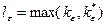 , и фиксируем такой член
, и фиксируем такой член 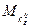 подпоследовательности
подпоследовательности 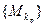 , номер которого
, номер которого  . Теперь при всех
. Теперь при всех 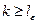 имеем:
имеем:
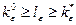
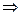
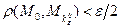 ;
; 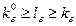 ,
, 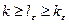
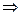
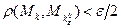 . Отсюда вытекает следующая цепочка неравенств:
. Отсюда вытекает следующая цепочка неравенств:
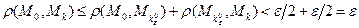 ,
,
т.е. точка 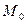 является пределом последовательности
является пределом последовательности 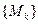 . ■
. ■
Из теорем 2.19 и 2.20 вытекает критерий сходимости последовательности.
Теорема 2.21(критерий сходимости Коши). Последовательность точек 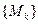 пространства
пространства 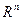 сходится тогда и только тогда, когда является фундаментальной последовательностью.
сходится тогда и только тогда, когда является фундаментальной последовательностью.
Дата добавления: 2016-06-05; просмотров: 2020;










