Дифференциальная форма теоремы Гаусса для напряженности электростатического поля в вакууме.

Теорема Гаусса для вектора напряженности электростатического поля 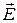может быть сформулирована и в дифференциальной форме, отражающей локальные свойства электростатического поля.

Действительно, рассмотрим поле точечного электрического заряда 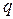, расположенного в начале координат:

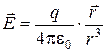. (1)

Из соотношения (1) следует

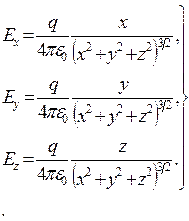(2)

Легко проверить непосредственным вычислением, что для 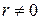, т.е. для точки наблюдения, в которой нет электрического заряда, справедливо соотношение:

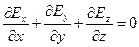. (3)

Математическая операция в левой части соотношения (3) имеет специальное название “дивергенция векторного поля 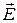” и специальное обозначение

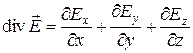. (4)

Очевидно, что результат (4) можно записать в форме:

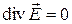. (5)

Нетрудно сообразить, что формула (5) будет иметь силу и для произвольного электростатического поля в каждой точке, где отсутствует электрический заряд.

Если в окрестности начала координат имеется объемная плотность электрического заряда 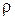, и рассматриваются расстояния от начала координат настолько малые, что величину 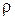можно считать постоянной величиной, то напряженность электростатического поля в окрестности начала координат может быть определена соотношением:

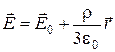, (6)

где 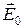- напряженность электростатического поля, создаваемого зарядами вне рассматриваемой окрестности - векторная постоянная величина (здесь использован результат (11) раздела 2.2.6.8 для напряженности электрического поля внутри шара с равномерным распределением заряда по объёму). В проекциях на оси декартовой системы координат имеем:

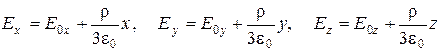. (7)

Вычисляя дивергенцию векторного поля (6)-(7) , получаем

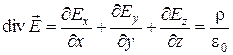. (8)

При 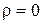из соотношения (8) следует соотношение (5). Подобное рассуждение можно провести в окрестности произвольной точки пространства. Таким образом, соотношение (8) является дифференциальной формой теоремы Гаусса для вектора напряжённости 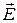электростатического поля в вакууме.

Для читателей, основательно владеющих методами векторного анализа, заметим, что для электрического заряда, распределенного в некотором объёме с объёмной плотностью 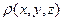, имеет место зависимость:

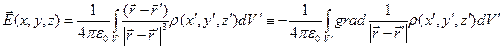(9)

Фактически при записи формулы (9) использована зависимость напряженности от потенциала электростатического поля. Вычислим дивергенцию полученного выражения:

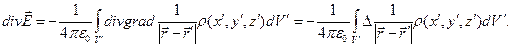(10)

В соотношениях (10) использовано обозначение лапласиана скалярной функции 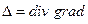. Далее используем известное соотношение векторного анализа

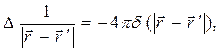(12)

и свойство дельта-функции Дирака

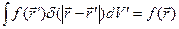, (13)

после чего получаем

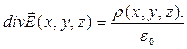(14)

Заметим, что дифференциальная форма теоремы Гаусса (14) для векторного поля 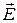непосредственно следует из интегральной формулировки (10) раздела 2.3.2.

Действительно, в силу математической теоремы Остроградского-Гаусса имеет место соотношение

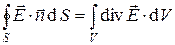, (15)

где 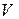- объем, ограниченный замкнутой поверхностью 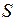. Если при этом величина электрического заряда в объеме 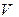может быть записана в форме

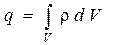, (16)

то из формулировки (10) предыдущего раздела, теоремы (15) и формулы (16) следует

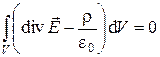. (17)

Поскольку соотношение (17) должно выполняться для произвольного объема (не только для какого-либо конкретного), то единственной возможностью выполнения условия (17) является обращение в нуль подынтегрального выражения, что приводит к соотношению (8).

Уравнение (8) записано в декартовой системе координат. С помощью теоремы (15) можно записать выражение для дивергенции векторного поля 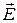в абстрактной символической форме

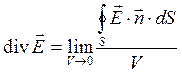. (18)

Выражение (18) служит также для установления математического и физического смысла операции дивергенции векторного поля:

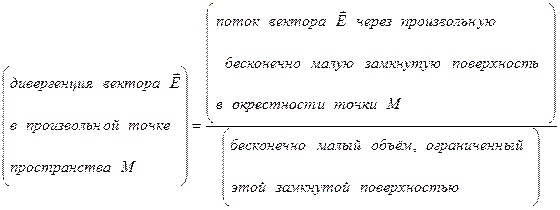
Если вспомнить определение потока вектора через замкнутую поверхность, то дивергенцию векторного поля можно определить как

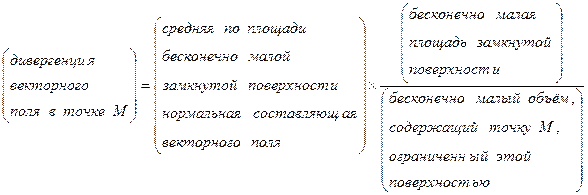
Выше было сказано, что эффективность применения теоремы Гаусса для векторного поля 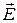существенно зависит от степени симметрии пространственного заряда. При этом речь шла об интегральной формулировке теоремы – формула (10) предыдущего раздела. Аналогичное явление имеет место и при рассмотрении дифференциальной формулировки теоремы Гаусса (8): она не является «замкнутой» в том смысле, что соотношением (8) связаны между собой три функции - 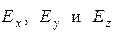, а уравнение всего одно единственное. Понятно, что только при наложении дополнительных связей между этими функциями можно будет определить каждую из них.

Оправданием столь подробного рассмотрения теоремы Гаусса для вектора напряженности электростатического поля служит большое значение, которое придают этой теореме в современной электродинамике.