Влияние чисел М и Re на характеристики компрессорных решеток

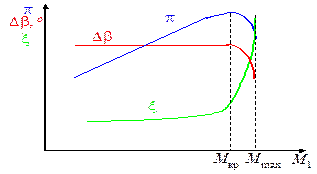1) М₁<М _кр . Течение в решетке профилей везде дозвуковое.

С ростом скорости набегающего потока:

- угол поворота практически не меняется Db=const.

- степень повышения давления p возрастает, т.к. растет кинетическая энергия потока, а следовательно, как это следует из уравнения Бернулли, и работа повышения давления L_п.

- коэффициент потерь несколько увеличивается из-за роста потерь на трение (больше энергии затрачивается на подтормаживание потока в п.с.)

2) М _кр < М₁ <М _max . При М₁=М _кр в межлопаточном канале появляется местная сверхзвуковая зона, замыкающаяся скачком уплотнения, что приводит к появлению волновых потерь. Крометого,взаимодействие скачков уплотне­ния с пограничным слоем может вызвать отрыв его от поверхности профиля. В результате наблюдается резкое увеличение коэффициента потерь x, уменьшение угла пово­рота потока Db и степени повышения давления p.

3) М₁ =М _max Область местных сверхзвуковых скоростей перекрывает "горло" межлопаточного канала. Дальнейшее увеличение числа M _w1 оказывается невозможным, т.к. расход воздуха через межлопаточный канал становится максимально возможным. Это явление называется запиранием решетки.

Число Рейнольдса, как известно, отражает соотношение между силами инерции и вязкости. При больших числах Re пограничный слой является тонким и его наличие (до точки отрыва, если она есть) не сказывается существенным образом на характере течения вне его.

Если изменение значения числа Re практически не влияет на картину течения, то такое течение называется автомодельным по числам Re.

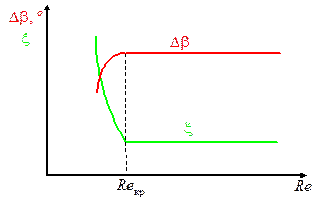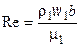
С уменьшением числа Re роль вязкого трения усиливается. Это приводит к набуханию пограничного слоя и увеличению длины его ламинарного участка. Начиная с некоторого значения Re=Re_кр происходит отрыв пограничного слоя от обтекаемой поверхности и, как следствие, рост потерь полного давления в решетке и некоторое снижение угла поворота потока и степени повышения давления, автомодельность по числам Re нарушается.