Регрессионный анализ

При корреляционном анализе с помощью коэффициента корреляции можно выяснить тесноту (силу) и направление связи, но нельзя узнать, как количественно меняется результативный признак при изменении факториального на единицу измерения. Эта задача решается с помощью регрессионного анализа.

Регрессия – это изменение результативного признака (зависимой переменной, или функции Y) при определённых изменениях факторного признака (независимой переменной или аргумента Х). Например, с изменением длины листа на 1 см его площадь изменяется на 4,6 см². Различают регрессию простую и множественную, по форме – линейную и криволинейную. Сущность регрессионного анализа состоит в том, чтобы построить линию (прямую в случае прямолинейной зависимости), которая наиболее точно выражала бы зависимость одного признака от другого.

Зависимость функции от аргумента при линейной регрессии выражается коэффициентом регрессии (в), который показывает, как в среднем изменяется (увеличивается или уменьшается, смотря по знаку в) результативный признак (функция) при изменении факториального признака (аргумента) на одну единицу измерения.

Коэффициенты линейной регрессии вычисляются по формулам:

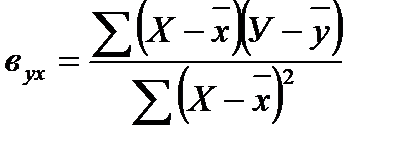и .

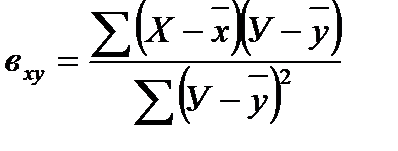Коэффициенты регрессии имеют знак коэффициента корреляции. Произведение коэффициентов регрессии равно квадрату коэффициентов корреляции (что используется для проверки расчётов коэффициентов регрессии):

;

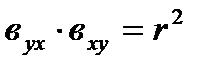Чаще всего из двух коэффициентов регрессии вычисляют только один. При исследовании односторонней зависимости, например корреляции между урожаем Y и количеством выпавших осадков Х (как в нашем примере), вычисляют только один коэффициент регрессии результативного признака 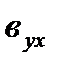, который показывает, как изменяется Y при изменении Х на единицу измерения; выражается он в единицах Y.

Так с увеличением количества осадков во II и III декадах июня на 1 мм урожайность яровой пшеницы повысится на 0,34 ц/га. Вычисление 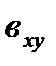лишено смысла, мы его рассчитали для проверки вычислений коэффициентов регрессии. Затем находят ошибку коэффициента регрессии:

_.

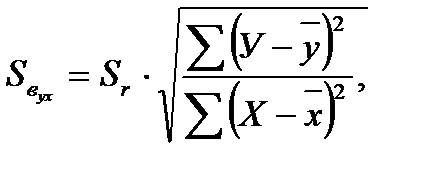
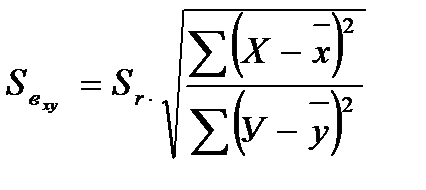Критерий существенности коэффициента регрессии равен:

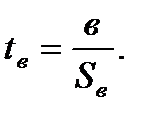
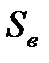и 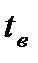мы не вычисляем, так как в данном примере 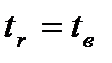, что свидетельствует о существенности регрессии.

Сопоставляя значения 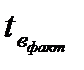и 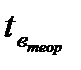можно при заданном уровне значимости (05 или 01) и числе степеней свободы v 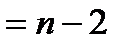оценить существенность коэффициента регрессии результативного признака – 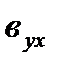. Если известен критерий существенности коэффициента корреляции 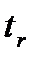и значимость его доказана, то существенным будет и коэффициент регрессии, так как .

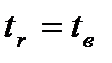После корреляционных и регрессионных анализов составляют уравнени регрессии, которые используют:

ü для вычисления неизвестного показателя по известному, например площади листьев по их длине;

ü для прогнозирования будущего урожая по числу цветков или завязей;

ü для прогнозирования качества урожая по элементам погоды;

ü для прогнозирования распространения вредителей и болезней по внешним условиям;

ü для прогнозирования качества продуктов переработки и их хранения по качеству сырья и т. д.

Связь между функцией и аргументом выражается уравнением регрессии или корреляционным уравнениям. При простой регрессии уравнением кратко обозначается Y=f (x) и при множественной Y=f (X,Z,V…). Если степень связи между признаками велика, то по уравнению регрессии можно предсказать значение результативного признака для определенных значений факториальных признаков. Для оценки тесноты связи используют коэффициенты корреляции и корреляционное отношение.

Совместное применение методов корреляции, регрессии и дисперсионного анализа для уточнения эксперимента получило название ковариационного анализа.

Для наглядности корреляцию можно изобразить в виде линии регрессии.

Теоретическую линию регрессии можно построить двумя способами:

- графическим (с помощью прозрачной линейки), позволяющим приближённо выявить лишь общую тенденцию зависимости;

- аналитическим, используя уравнение линейной регрессии Y по Х:

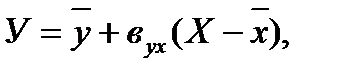
где 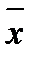и 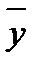– средние арифметические признаков Х и Y;

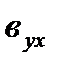–коэффициент регрессии результативного признака.

Подставляя в это уравнение вычисленные значения 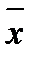, 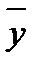и 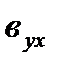_, определяют формулу уравнения прямой линии ;

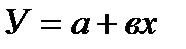Суть ковариационного анализа сводится к следующему. Если между результативным признаком Y и сопутствующим эксперименту не изучаемым признаком Х имеет место значимая линейная связь, то методом ковариации можно статистически выровнять условия проведения опыта в отношении признака Х и тем заметно снизить ошибку эксперимента и получить больше информации об изучаемом явлении.