Гармонические колебания

Сила упругости

Эта сила обусловлена электромагнитным взаимодействием между частицами вещества (молекулами). Она возникает внутридеформированного тела при действии на него внешней силы 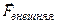. При этом .

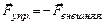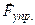Природа силы упругости. - сила электромагнитного взаимодействия 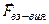между частицами вещества. Рассмотрим зависимость 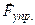от расстояния r между центрами соседних частиц. Как известно, атомы твёрдого тела образуют кристаллическую решётку, характеризуемую постоянной решётки 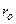(среднее расстояние между центрами атомов в данном направлении). Между соседними частицами действуют одновременно две электростатические силы: притяжения и отталкивания. При попытке сблизить частицы на расстояние r<r_o преобладает сила отталкивания ( 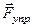> 0), при разнесении частиц на r>r_o преобладает сила притяжения ( 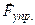<0). С увеличением температуры t^o глубина потенциальной “ямы” уменьшается и, при t^o=t^о_пл., ²яма² на кривой 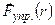исчезает.

С точки зрения "поведения" тела, после прекращения действия внешней силы, деформации разделяют на упругие и пластичные. С точки же зрения смещения атомов относительно друг друга, различают следующие виды деформаций: 1) сжатие (растяжение), 2) изгиб; 3) сдвиг; 4) кручение. Причём, изгиб сводится к сжатию, а кручение – к сдвигу. Из рисунка видно, что при изгибе верхние слои стержня растягиваются, а нижние сжимаются; средние же - деформации не испытывают. Поэтому сердцевину стержня можно удалить без снижения его прочности, что и имеет место: 1) в технике (используют трубы, а не сплошные стержни); 2) у злаковых растений стебли трубчатые; 3) трубчатые кости у животных; 4) молодые листья свёрнуты трубочкой; 5) лист бумаги при переносе сворачивают, для прочности, в трубочку и т. п.

Закон Гука (справедлив для упругих деформаций) описывает зависимость 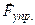от величины деформации Dl, свойств вещества и размеров тела. Открыт в 1660 г. англичанином Робертом Гуком, который опытным путём установил, что:

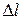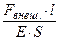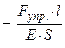= = Þ

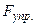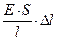= - = -k ,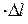

где k - коэффициент жёсткости образца (тела), Е - модуль Юнга, характеризует упругие свойства вещества.

Закон Гука: 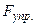= -k 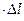- сила упругости пропорциональна деформации Dl и направлена противоположно (знак “-“) внешней силе.

Сила сухого трения

Возникает на границе двух тел и препятствует их относительному смещению. Сила трения 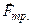направлена по касательной к поверхности соприкасающихся тел противоположно скорости скольжения данного тела (отсюда и термин "трение скольжения"), т.е. 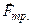препятствует смещению одного тела относительно контактирующего с ним другого.

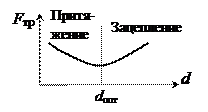Причины возникновения 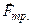: а) при больших неровностях 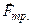обусловлена зацеплением неровностей поверхностей; б) при малых неровностях (когда расстояние между поверхностями d сравнимо с r_o) 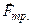обусловлена силами межмолекулярного притяжения.

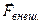При действии на тело сила трения может возникать и при относительном покое касающихся тел. Такую 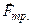называют силой трения покоя 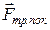, причём в момент начала скольжения > .

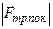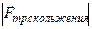Законы трения впервые были установлены итальянским художником Леонардо да Винчи » 500 лет назад, но … не были опубликованы. Повторно они были открыты в XVIII в. французскими физиками Амонтоном и Кулоном:

1) F_тр =m×N (где m-коэффициент трения для данной пары тел; N-сила нормального давления; не всегда N=mg!). Сила трения отлична от нуля только при N>0 и F_t>0, где F_t - сила, действующая вдоль поверхности;

2) F_тр не зависит (!) от площади контакта тел (при данной силе нормального давления N);

Особенности силы сухого трения:

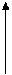1) Наличие силы трения-покоя 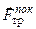(в жидкостях и газах 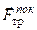= 0);

2) Зависимость 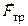от размеров шероховатостей d и относительной скорости контактирующих тел;

3) Скользящее тело (т.е. при J¹0) может быть смещено вбок (!) сколь угодно малой внешней силой, т.к. при J¹0 боковое воздействие приводит к увеличению J, в результате 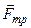уменьшается. Например: а) занос (skid) автомобиля при его резком торможении; б) соскакивание ремня со шкива двигателя при его резком торможении; в) вытаскивание гвоздя из доски «голыми» руками при его повороте по и против часовой стрелки.

Гармонические колебания

Колебательное движение - это такое движение, при котором система, многократно отклоняясь от состояния своего равновесия, вновь и вновь возвращается к нему. Колебания называют периодическими, если возврат совершается через равные промежутки времени Т (период колебаний).

Примеры колебательного движения: вибрация струны, движения поршня двигателя, морские приливы и отливы, биение сердца, дыхание, тепловые колебания атомов в кристаллах, переменный ток и т.п.

Замечательно то, что различные по природе колебания описываются одними и теми же уравнениями.

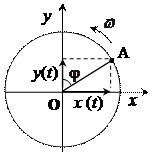Рассмотрим простейшее колебательное движение: изменение проекции радиус-вектора длиной А на одну из осей при его равномерном вращении.

Величина проекции радиус-век-тора на ось x изменяется со временем по закону: 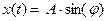. Но 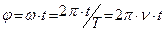, тогда:

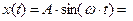
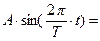
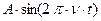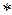. ( ) Это и есть уравнение гармонических колебаний. Если рассмотреть изменение проекции радиус-вектора на ось у, то уравнение ( 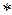) вместо функции sinсодержало бы функцию cos.

Терминология: Т и n-период (время одного полного колебания) и частота колебаний (число колебаний за 1 с); w - циклическая (круговая) частота (число колебаний за 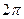секунд); фаза (j) - выражение, стоящее под знакомsin (или cos).Физический смысл фазы состоит в том, что онаопределяет состояние колебательной системы в данный момент времени; начальная фаза ( 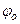) - значение j при 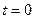(обычно выбирают 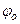=0).

Проследим за изменением фазы со временем, принимая во внимание, что: .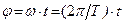

t		T/4	T/2	T	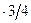T

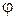
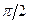
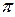
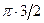
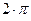
Определим скорость изменения проекции радиус-вектора: 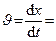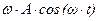= 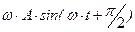, т.е. изменения скорости отстают по фазе от изменений координаты на p/2.

Так как 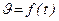, то ускорение 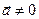. Найдём его: а =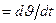 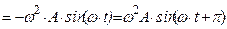= 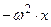, т.е. изменения ускорения отстают по фазе изменений координаты на p/2.

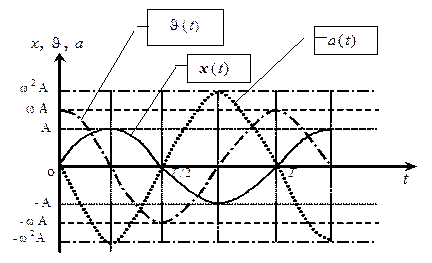
Для чего же было введено такое понятие как “гармонические колебания”?

Теорема Фурье: любой реальный сигнал можно представить в виде конечной суммы гармонических колебаний с различными амплитудами и частотами. Эту сумму называют гармоническим спектром данного сигнала.

Гармонический спектр является «паспортом» сигнала, позволяющим однозначно узнать (идентифицировать) его среди множества других сигналов одинаковой природы (звуковых, электрических, оптических сигналов).