Процессы всасывания и нагнетания поршневых насосов

Процесс всасывания.Особенность всасывания поршневого насоса, в отличие от центробежного, заключается в том, что скорость движения жидкости во всасывающей трубе не остается постоянной с течением времени. Она изменяется пропорционально переменной скорости движения поршня. Из графика на рис. 6.27, а видно, что в первую половину хода поршня скорость его увеличивается от нуля до максимума, во вторую – уменьшается от минимума до нуля.

При нормальной работе насоса всасываемая жидкость неразрывно следует за поршнем. Поэтому в первую половину хода поршня жидкость во всасывающей трубе движется ускоренно, а во вторую – замедленно.

Часть напора 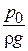, соответствующего давлению на свободной поверхности питательного бака (рис. 6.23), в первую половину хода поршня затрачивается на сообщение жидкости ускорения. Благодаря этому разрежение под поршнем увеличивается. Во второй половине хода поршень наоборот движется замедленно, с отрицательным ускорением, жидкость тормозится замедляющим своё движение поршнем, и давление под поршнем возрастает. На рис. 6.28 представлена схема всасывающей линии поршневого насоса.

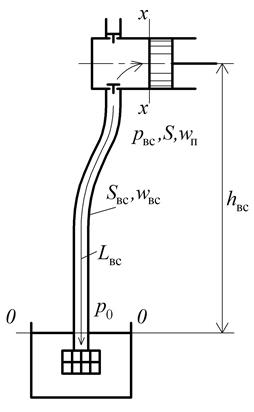
Рис. 6.28. Схема всасывающей линии поршневого насоса

Запишем уравнение Бернулли для сечений 0–0 и х–х:

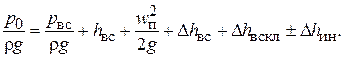(6.63)

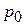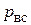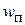Здесь – давление на свободной поверхности питательного бака, – давление в полости насоса, – высота всасывания, – скорость движения поршня, 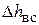– суммарные гидравлические потери всасывающей линии, 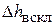– гидравлические сопротивления всасывающего клапана, 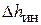– напор, затрачиваемый на преодоление инерционного сопротивления жидкости благодаря неустановившемуся характеру ее движения во всасывающей линии.

Рассмотрим каждый член уравнения (6.63) в отдельности.

Довольно часто 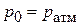. В химической технологии встречаются случаи, когда питательный бак закрыт. В этом случае с течением времени давление 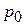будет уменьшаться. Предполагая, что объем воздуха над жидкостью в питательном баке 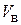меняется по изотерме, получим формулу для расчета давления :

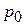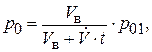(6.64)

где 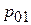– первоначальное давление воздуха над жидкостью, 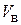– первоначальный объем воздуха над жидкостью, 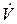– подача насоса, 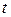– время наблюдения.

Давление 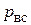должно быть меньше давления 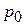, иначе не будет всасывания. Чем меньше 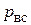, тем лучше условия для всасывания. Нижний предел давления 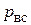обусловлен кавитацией. Если 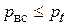(давление парообразования жидкости при данной температуре), будет кавитация
и наступит ударная работа насоса. Поршень в момент всасывания оторвется от жидкости, и в начале нагнетания произойдет удар поршня
о жидкость. Следовательно, крайнее значение .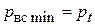

Высота всасывания в уравнении (6.63) является искомой величиной. Скоростной напор поршня 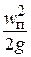меняется по закону синуса:

w_п²/2g = (wrsinj)²/2g. (6.65)

Так как жидкость во всасывающей трубе движется непрерывно вслед за поршнем, то исходя из условия неразрывности потока получим выражение для скорости жидкости во всасывающей трубе:

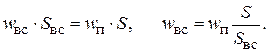
Определим суммарное гидравлическое сопротивление всасывающей линии :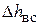

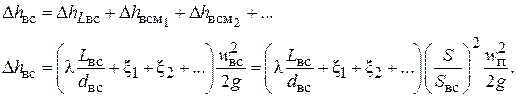(6.66)

Как видно из выражения (6.66), 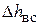, как и скоростной напор поршня, меняется по закону синуса.

Гидравлическое сопротивление всасывающего клапана 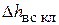определяется по формуле:

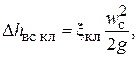(6.67)

где 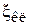– коэффициент сопротивления клапана, 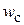– скорость жидкости при прохождении через седло клапана. Скорость 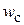определяется
из условия неразрывности:

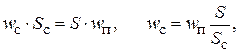
где 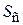– площадь поперечного сечения седла. Тогда получим:

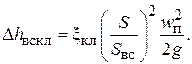(6.68)

Как видно из выражения (6.68), 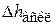меняется по закону синуса.

Рассмотрим инерционные потери напора 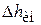. Сначала найдем массу жидкости, находящейся во всасывающей линии длиной 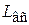, и её ускорение:

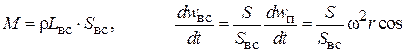j.

Согласно второму закону Ньютона найдем силу инерции :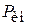

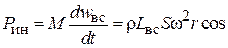j.

Относя силу инерции к площади всасывающей линии и к rg, получим выражение для инерционного напора :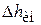

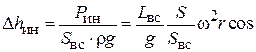j. (6.69)

Итак, инерционный напор меняется по закону косинуса.

Как известно, при j = 0, sin j = 0, cos j = 1,

при j = p/2, sin j = 1, cos j = 0,

при j = p, sin j = 0, cos j = –1

и т.д.

Расчеты показывают, что

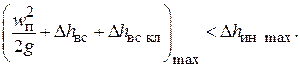
Поэтому анализ уравнения (6.63) проведем при максимальном значении инерционного напора 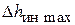, т.е. при j = 0. Тогда будем иметь:

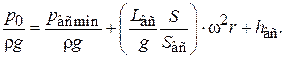(6.70)

При j = 0 инерционный напор имеет максимальное значение, это положение поршня наиболее опасное с точки зрения закипания жидкости, так как давление в полости насоса имеет минимальное значение .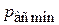

Уравнение (6.70) позволяет решить задачи:

– определение допустимой высоты всасывания при ;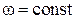

– определения допустимого числа оборотов вала кривошипа
при ;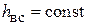

Определим высоту всасывания. Максимальное значение 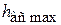определяется при :

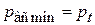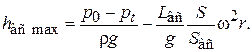(6.71)

Допустимое значение :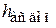

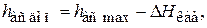(6.72)

где 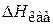– кавитационный запас.

Допустимая высота всасывания для воды при нормальных условиях не превышает 4,0–5,5 м.

Определим частоту вращения вала кривошипа. Из уравнения (6.70) получим:

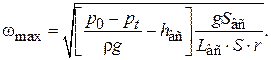(6.73)

Допустимое значение 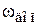должно быть меньше максимального .

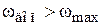Разумеется, возможна постановка задач определения предельных значений 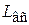, 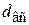и других параметров насоса.