Электронная теплоемкость

Рассмотрим простейший случай. Из классических представлений электронный газ можно рассматривать как идеальный газ. К последнему применим закон равномерного распределения энергии по степеням свободы. То есть на каждый электрон приходиться 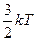энергии. Тогда, исходя из классических представлений, мы будем иметь суммарную теплоемкость

.

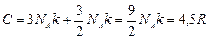Полученное выражение не соответствует экспериментальным данным как для металлов, у которых высокая концентрация внешних электронов, так и для диэлектриков, для которых она стремится к нулю. В области высоких температур для всех твердых тел эксперимент дает примерно одинаковую теплоемкость, приблизительно равную 3R. То есть наше предположение о применимости к электронному газу классических представлений (в частности, закона равномерного распределения энергии по степеням свободы) является неправомерным.

Дело в том, что при определении электронной теплоемкости необходимо учитывать квантово-механический характер поведения электронов в решетке. Поэтому для нахождения вклада электрона в суммарную теплоемкость необходимо учитывать не все электроны данного кристалла, а лишь те, которые лежат в полосе шириной kT вблизи уровня Ферми. С учетом таких электронов электронная теплоемкость может быть представлена в виде . Тогда суммарная теплоемкость при низких температурах может быть представлена в виде:

,

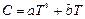где а и b - постоянные множители.

Таким образом, вблизи абсолютного нуля теплоемкость, связанная с колебаниями решетки, падает пропорционально Т³, а теплоемкость, обусловленная электронным газом, изменяется линейно. Поэтому вклад теплоемкости электронов при значительном понижении температуры становится определяющим.

Теплопроводность