Орбитальный магнитный и механический момент электрона

Всякий атом представляет собой динамическую систему, состоящую из ядра и электронного облака. Каждый электрон обладает определенным спиновым магнитным моментом Р_сп, кроме того, движение электрона по некоторой замкнутой орбите внутри атома создает так называемый орбитальный магнитный момент Р_орб . Следовательно, полный магнитный момент атома Р_ат будет представлять геометрическую сумму орбитальных и спиновых магнитных моментов электронов, принадлежащих данному атому

,

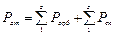где z - число электронов в атоме.

Рассмотрим процессы в атомах, молекулах и кристаллах, которые определяют принадлежность данного вещества к одному из пяти видов магнетиков. Для этого выясним сначала соотношение между магнитным и механическим моментами электрона.

Электрон, вращающийся вокруг ядра с частотой n, по своему магнитному действию эквивалентен круговому току. Магнитный момент этого тока и есть орбитальный магнитный момент электрона, модуль которого равен:

,

где 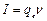- сила тока, 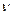- частота вращения, S - площадь орбиты электрона.

Если электрон движется по часовой стрелке, то ток направлен против часовой стрелки и вектор 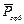в соответствии с правилом правого винта направлен перпендикулярно плоскости орбиты электрона (см. рисунок 9.1).

С другой стороны, движущийся по орбите электрон обладает механическим моментом импульса, модуль которого равен:

,

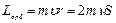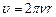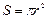где , а . Вектор 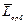, направление которого также подчиняется правилу правого винта, называется орбитальным механическим моментом электрона.

Векторы 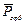и 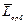жестко связаны и всегда противоположны (см. рисунок 9.1) (так как направление тока противоположно направлению движения электрона), поэтому поворот одного из векторов обязательно сопровождается таким же поворотом другого вектора.

Отношение магнитного момента к механическому называется гиромагнитным отношением орбитальных моментов:

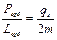
В полученную формулу не входит номер орбиты электрона п. Следовательно, орбитальное гиромагнитное отношение одинаково для любой электронной орбиты. Формула выведена для круговой орбиты электрона, но можно доказать, что она справедлива и для любой эллиптической орбиты.

Экспериментальное определение гиромагнитного отношения было проведено в опытах Эйнштейна и де Гааза, которые наблюдали поворот свободно подвешенного на тончайшей кварцевой нити железного стержня при его намагничивании во внешнем магнитном поле. Значение гиромагнитного отношения, найденное в этих опытах, оказалось равным 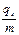, т. е. в два раза больше, чем определенное ранее.

Для объяснения этого результата было предположено, а впоследствии доказано, что кроме орбитальных моментов электрон обладает собственным механическим моментом импульса 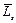, называемый спином. Спину электрона соответствует спиновой магнитный момент .

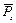Величина спинового орбитального момента в два раза больше орбитального:

.

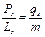Важнейшей особенностью спина электрона является то, что в магнитном поле спин может быть ориентирован только двумя способами: либо параллельно напряженности поля, либо антипараллельно.