Соединение потребителей треугольником

В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз

(3.32)

P = P_ab + P_bc + P_ca,

где

(3.33)

P_ab = U_ab I_ab cos φ_ab; P_bc = U_bc I_bc cos φ_bc; P_ca = U_ca I_ca cos φ_ca;
U_ab, U_bc, U_ca; I_ab, I_bc, I_ca – фазные напряжения и токи;
φ_ab, φ_bc, φ_ca – углы сдвига фаз между напряжением и током.

Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз

(3.34)

Q = Q_ab + Q_bc + Q_ca,

где

(3.35)

Q_ab = U_ab I_ab sin φ_ab; Q_bc = U_bc I_bc sin φ_bc; Q_ca = U_ca I_ca sin φ_ca.

Полная мощность отдельных фаз

(3.36)

S_ab = U_ab I_ab; S_bc = U_bc I_bc; S_ca = U_ca I_ca.

Полная мощность трехфазного приемника

(3.37)

.

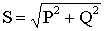При симметричной системе напряжений (U_ab = U_bc = U_ca = U_Ф) и симметричной нагрузке (I_ab = I_bc = I_ca = I_Ф; φ_ab = φ_bc = φ_ca = φ) фазные мощности равны P_ab = P_bc = P_ca = P_Ф = U_Ф I_Ф cos φ; Q_ab = Q_bc = Q_ca = Q_Ф = U_Ф I_Ф sin φ.

Активная мощность симметричного трехфазного приемника

P = 3 P_Ф = 3 U_Ф I_Ф cos φ.

Аналогично выражается и реактивная мощность

Q = 3 Q_Ф = 3 U_Ф I_Ф sin φ.

Полная мощность

S = 3 S_Ф = 3 U_Ф I_Ф.

Так как за номинальные величины обычно принимают линейные напряжения и токи, то мощности удобней выражать через линейные величины U_Л и I_Л.

При соединении фаз симметричного приемника звездой U_Ф = U_Л / 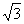, I_Ф = I_Л, при соединении треугольником U_Ф = U_Л, I_Ф = I_Л / 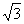. Поэтому независимо от схемы соединения фаз приемника активная мощность при симметричной нагрузке определяется одной и той же формулой

(3.38)

P = 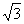U_Л I_Л cos φ.

где U_Л и I_Л – линейное напряжение и ток; cos φ – фазный.

Обычно индексы "л" и "ф" не указывают и формула принимает вид

(3.39)

P = 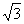U I cos φ.

Соответственно реактивная мощность

(3.40)

Q = 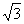U I sin φ.

и полная мощность

(3.41)

S = 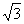U I.

При этом надо помнить, что угол φ является углом сдвига фаз между фазными напряжением и током, и, что при неизмененном линейном напряжении, переключая приемник со звезды в треугольник его мощность увеличивается в три раза:

Δ P = Υ 3P.