Мост Максвелла-Вина.

В модификации моста Максвелла предложенной Вином для измерения неизвестной индуктивности используется параллельное соединение сопротивлений и емкостей.

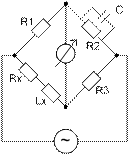
Поскольку ток через конденсатор опережает ток через индуктивность, необходима фазовая компенсация. Следовательно, емкостные и индуктивные компоненты следует размещать в противоположных плечах моста. Условие равновесия моста:

Rx=R1R3/R2 (7)

Lx=R1R3/C (8)

Qx=ωLx/Rx=ωR2C (9)

Индуктивность измеряется с помощью емкостей высокого качества, которые значительно точнее и легче в изготовлении, чем образцовые, и создают незначительное поле. Равновесие обычно достигается регулировкой R2 и С, т.к. этим обеспечивается независимое уравновешивание Rx и Lx. Однако можно использовать фиксированную С и регулировать R2, R1 или R3, хотя при этом время уравновешивания возрастает. Мост широко используется для измерения индуктивности катушек с добротностью Q ниже 10. Этот верхний предел Q обусловлен тем, что как следует из (3) сумма фазовых углов противоположных плеч моста должны быть равны при равновесии. Т.к. R1 и R3 активные сопротивления, то их фазовые углы равны нулю. Ток через индуктивность с большой Q будет отставать по фазе почти на 90⁰. это означает, что резистор R2 должен иметь слишком большое сопротивление. Эта трудность преодолена в мосте Хея.

Мост Хея.

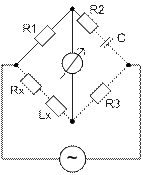
Rx=R1R3/R2(1+Q²x) (10)

Lx=R1R3C/(1+1/Q²x) (11)

Qx=ωLx/Rx=1/ωR2c (12)

(10) и (12) – условие равновесия

R2 соединен последовательно с емкостью С. При высокой добротности Lx R2 можно выбрать очень маленьким. Недостаток: равновесие зависит так, что шкалу прибора невозможно проградуировать в значениях индуктивности. Мост Хея обычно используют только для измерения катушек с добротностью Q меньше 10. если пренебречь в (11) членом Q²x, то значение индуктивности не зависет от частоты, и погрешность составит менее1%.

Мост Оуэна.

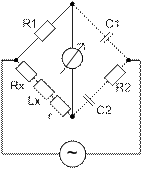
Rx=(R1C1/C2)-r (13)

Lx=R1R2C1 (14)

(13) и (14) условие равновесия моста. Если R2 и С2 регулируемые элементы схемы, то можно обеспечить независимое равновесие для Rx и Lx. Хотя это возможно для регулировки R1 и R2. r подключать необязательно, нужно для расширения диапазона возможного баланса сопротивлений. Данный мост полезен для определения дифференциальной индуктивности.

Мост Кемпбелла.

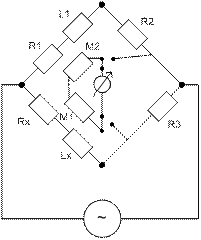
Mx=M1R3/R2 (15)

Rx=R1R3/R2 (16)

Lx=L1R3/R2 (17)

Используют для измерений взаимной индуктивности со сравнением с образцовой. (15) и (17) - условие равновесия. Положение 2: калибровка регулированием L1 и R1. Положение 1: измерение. М1 регулируют до установления с Мх.

Измерение индуктивности, добротности, емкости, тангенс дельта мостами переменного тока

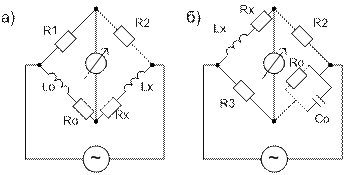
Мостовые схемы измерения индуктивности и добротности с образцовыми элементами: а) - с катушками, б) с конденсатором. В них используется источник гармонического тока с напряжением U и угловой частотой ω. Эти мосты обеспечивают наилучшее уравновешивание. Эквивалентная схема замещения для катушек индуктивности с потерями могут быть последовательными или параллельными в зависимости от потерь отраженных активным сопротивлением. Условие равновесия моста для схемы а): R1(Rx+jωLx)=R2(Ro+jωLo) (1).

Где Lх и Rх измеряемое индуктивность и сопротивление омических потерь в катушке, Lo и R0 - образцовая индуктивности и сопротивление. Приравняв, действительные и мнимые части в выражении (1) находим: Rx=RoR2/R1, Lx=LoR2/R1 (2).

Поскольку изготовление высокодобротных образцов катушек вызывает определенные трудности, часто в качестве образцовой меры в мостах переменного тока применяют конденсатор (рис б). Для этой схемы справедливо: Rx+jωLx=R2R3(1/Ro+jωCo) (3).

Если в данном уравнении приравнять действительную и мнимую части, то получим следующее выражение: Rx=R2R3/Ro Lx=CoR2R3 (4).

Добротность катушки определяется: Q=ωLx/Rx=RoωCo (5)