Цифровые измерительные приборы (ЦИП)

Появление и интенсивное развитие ЦИП (середина XX в.), обладающих целым рядом преимуществ по сравнению с аналоговыми (высокая точность измерения, широкий диапазон, индикация результатов в цифровой форме, быстродействие, возможность ввода информации в ЭВМ и цифропечатающие устройства, автоматический процесс измерения, управление рядом работ, выбором пределов измерения), поставили вопрос о дальнейшем пути развития электроизмерительной техники вообще.

ЦИП характеризуется двумя особенностями: наличием операций аналого-цифрового преобразования сигналов и цифрового отображения результата измерения. Технически реализуются эти операции с помощью аналого-цифровых преобразователей АЦП и блока регистрации БР с цифровым отсчетным устройством, который служит для представления результата в цифровой форме (рис. 9.10). В состав ЦИП входят также входные аналоговые преобразователи – входные устройства ВУ,простые – масштабные (делители, усилители) и сложные – функциональные (преобразователи u_~ в U₌, преобразователи Р в U₌ ). В приборы с цифровой обработкой информации входит также арифметическое устройство АУ для выполнения вычислительных операций. Работу всех узлов прибора синхронизирует блок управления БУ. Между АЦП и АУ, а также между АУ и БР могут устанавливаться преобразователи кода (ПК). БУ задает моменты дискретизации входных сигналов. Он же задает режим работы АУ, на информационные входы которого поступают коды мгновенных значений с АЦП.

Необходимо отметить, что преобразование дискретной величины в код присуще любому процессу измерения в смысловом значении. В аналоговых приборах преобразование осуществляет человек. В цифровых приборах это преобразование происходит без участия человека – автоматически.

Поэтому общим отличительным признаком ЦИП является автоматизация преобразования. При преобразовании непрерывной величины в код неизбежны методические погрешности за счет дискретизации и квантования.

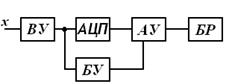
Рис. 9.10. Структурная схема цифрового измерительного прибора

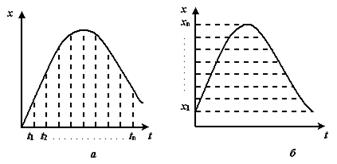
Рис. 9.11. Операции преобразования непрерывной величины в код: дискретизация (а)

и квантование (б)

Дискретизация – операция преобразования, при которой мгновенные значения непрерывной величины сохраняются только в определенные моменты времени (рис. 9.11,а).

Квантование – операция преобразования, при которой осуществляется замена мгновенных значений непрерывной величины фиксированными уровнями (рис. 9.11,б).

Известно из теоремы Котельникова, что сигнал с ограниченным спектром может быть точно восстановлен по его мгновенным значениям в дискретных точках, если частота дискретизации вдвое превышает граничную частоту сигнала. Для сигналов неограниченного спектра с убывающими амплитудами эта теорема приближенно определяет «порог» восстановления, но ничего не говорит о точности восстановления, которая определяется как раз отбрасываемыми высокочастотными составляющими. Поэтому оценку погрешности дискретизации необходимо выполнять иными методами.

Погрешность квантования определяется размером шага квантования, т.е. числом разрядов АЦП. Эта погрешность, обусловленная нахождением мгновенного значения между уровнями квантования, имеет случайный характер и может быть отнесена к помехам.

Пусть необходимо измерить некоторую величину X. Можно сде­лать это несколькими способами.

Первый способ заключается в сравнении измеряемой величины X с известной мерой, повторяющейся до тех пор, пока вес X не сравняется с весом по q. Характерная черта метода – последовательный счет повторяющейся мелкой единичной меры – кванта до приближения получаемой суммы ц к значению измеряемой величины X (рис. 9.12,а).

Разновидностью такого способа измерения является последовательный счет повторяющейся измеряемой величины X до приближения получаемой суммы к значению крупной меры q,. кратной кванту Х (рис.9.12.б).

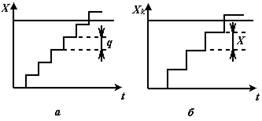
Рис. 9.12. Метод последовательного счета

Этот метод называют методом последовательного счета (рис. 9.12).

Второй способ заключается в сравнении измеряемой величины X с известными мерами Х_к, значения которых могут изменяться в соответствии с весовыми коэффициентами двоичного кода 2⁰ , 2¹, 2², 2³ и т.д. Сначала сравнивают наибольшую меру. Если она меньше, то ее оставляют и добавляют следующую по порядку убывания. Дальше сравнивают с X сумму Х_к и т.д. (рис. 9.13).

Если наибольшая мера оказалась больше X, то вместо нее ставят меньшую по степени убывания меру. Дальше процесс становится ясным. Характерная черта метода – наличие нескольких мер, кратных кванту и соотносящихся как весовые коэффициенты кода. Результаты сравнения (больше, меньше) определяют состояние в разрядах кода в направлении от старших к младшим. В нашем случае 0101. Этот метод называется кодо-импульсным или методом поразрядного уравновешивания.

Третий способ заключается в сравнении измеряемой величины X одновременно со многими мерами, кратными кванту q. Выделяется подмножество мер, меньшее X,и мерам приписывается 1, для остальных – 0. Образуется единичный код числа N, выражающий значение X в единицах q. Характерная черта метода – одновременное сравнение измеряемой величины X со множеством мер. Этот метод называют методом считывания (рис. 9.14).

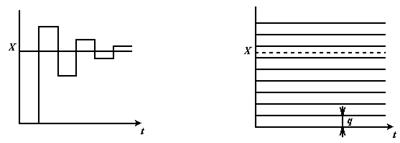
Рис. 9.13. Метод поразрядного уравновешивания Рис. 9.14. Метод считывания

Отметим, что X может быть как электрической, так и неэлектрической величиной. С помощью преобразователей эти величины преобразуются в выходную величину Y, ограниченную, как правило, интервалом времени ∆t(Y=∆t), частотой следования импульсов f(Y=f), напряжением U(Y=U), угловым или линейным перемещением (Y=а; Y=l).

Первый способ ограничивает самое низкое быстродействие, а третий обеспечивает максимальное быстродействие, но требует больших аппаратных затрат.

Всегда необходимо иметь в виду, что никакая система не может быть оптимальной во всех отношениях. Оптимальность достижима в определенном смысле. Используемые в ЦИП АЦП оценивают по двум основным критериям: быстродействию и погрешности преобразования. Эти критерии взаимно противоречивы.