Случай одинаковой совокупности параметров g при разных значениях l
Вернемся к детализации правила решения u*(х) из (6.5.10) и обсуждению его взаимосвязи с адаптивным байесовым правилом решения. Рассмотрим сначала распространенный случай, когда для всех значений  совокупности параметров
совокупности параметров 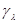 одинаковы и совпадают с полной совокупностью
одинаковы и совпадают с полной совокупностью  . При этом
. При этом
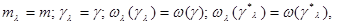 (6.5.13)
(6.5.13)
где 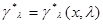 - решение уравнения правдоподобия (6.5.4), вообще говоря, разное при разных значениях
- решение уравнения правдоподобия (6.5.4), вообще говоря, разное при разных значениях  . Однако постольку, поскольку величины
. Однако постольку, поскольку величины 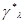 представляют собой оценки одних и тех же параметров
представляют собой оценки одних и тех же параметров  , истинные значения которых не изменяются при изменении
, истинные значения которых не изменяются при изменении  , то в случае состоятельности этих оценок (напомним, что решение уравнения правдоподобия удовлетворяет требованию состоятельности) и близости их к истинным значениям
, то в случае состоятельности этих оценок (напомним, что решение уравнения правдоподобия удовлетворяет требованию состоятельности) и близости их к истинным значениям  величины
величины 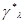 слабо зависят от
слабо зависят от  и не могут отличаться сильно друг от друга при разных значениях
и не могут отличаться сильно друг от друга при разных значениях  . Возможные отличия
. Возможные отличия 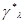 при
при 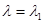 и
и 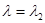 , где
, где 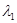 и
и 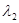 - любые два значения
- любые два значения  , они обусловлены только случайным отклонением этих оценок от истинного значения
, они обусловлены только случайным отклонением этих оценок от истинного значения  , одинакового при
, одинакового при 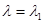 и
и 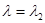 .
.
Эти случайные отклонения характеризуются матрицей 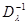 из (6.5.6), которая представляет собой асимптотическую апостериорную корреляционную матрицу для величин отклонений
из (6.5.6), которая представляет собой асимптотическую апостериорную корреляционную матрицу для величин отклонений 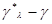 и, вообще говоря, зависит от
и, вообще говоря, зависит от  . Однако если функция
. Однако если функция  изменяется медленно, так что выполняется второе из неравенств (6.5.7), то величина
изменяется медленно, так что выполняется второе из неравенств (6.5.7), то величина 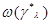 из (6.5.13) практически не зависит от
из (6.5.13) практически не зависит от  (зависит значительно слабее, чем любая другая функция
(зависит значительно слабее, чем любая другая функция  , входящая в подынтегральное выражение (6.5.8)). Благодаря этому ее можно сократить в числителе и знаменателе (6.5.8) или, что то же самое в данном случае, определить функцию
, входящая в подынтегральное выражение (6.5.8)). Благодаря этому ее можно сократить в числителе и знаменателе (6.5.8) или, что то же самое в данном случае, определить функцию 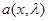 , входящую в (6.5.8), следующим образом:
, входящую в (6.5.8), следующим образом:
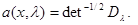 (6.5.14)
(6.5.14)
Получающееся с учетом равенства (6.5.14) упрощение для выражения апостериорного риска (6.5.8) является весьма существенным. Оказывается, что при одинаковой для всех значений  совокупности параметров
совокупности параметров  и при выполнении единственного условия плавности изменения функции
и при выполнении единственного условия плавности изменения функции  количественно это условие задается неравенством (6.5.7), апостериорный риск и правило решения u*(х) вообще не зависят от
количественно это условие задается неравенством (6.5.7), апостериорный риск и правило решения u*(х) вообще не зависят от  . Само оптимальное решение находится минимизацией выражения (6.5.8) при подстановке в него функции
. Само оптимальное решение находится минимизацией выражения (6.5.8) при подстановке в него функции 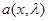 из (6.5.14).
из (6.5.14).
Рассматриваемый здесь случай одинаковой для разных  , совокупности неизвестных параметров
, совокупности неизвестных параметров  может иметь место как при дискретном, так и при непрерывном множестве значений
может иметь место как при дискретном, так и при непрерывном множестве значений  .
.
Для непрерывного множества значений  этот случай наиболее характерен; более того, трудно представить себе не слишком искусственный пример, когда плотность вероятности
этот случай наиболее характерен; более того, трудно представить себе не слишком искусственный пример, когда плотность вероятности 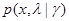 для разных значений
для разных значений  , из непрерывного множества значений зависит от разных совокупностей параметров
, из непрерывного множества значений зависит от разных совокупностей параметров  (например,
(например, 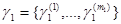 при
при 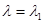 и
и 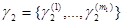 при
при 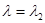 ). Для непрерывного множества значений
). Для непрерывного множества значений  процедуру нахождения правила решения u*(х), соответствующего минимуму усредненного риска, можно детализировать дальше и, кроме того, можно показать, что получающееся при этом правило решения совпадает асимптотически с адаптивным байесовым правилом решения, полученным выше.
процедуру нахождения правила решения u*(х), соответствующего минимуму усредненного риска, можно детализировать дальше и, кроме того, можно показать, что получающееся при этом правило решения совпадает асимптотически с адаптивным байесовым правилом решения, полученным выше.
Воспользуемся для этого асимптотическим приближением (6.3.2) для функции 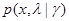 , из которого следует, что входящие в выражение (6.5.8) для апостериорного риска функции
, из которого следует, что входящие в выражение (6.5.8) для апостериорного риска функции 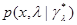 и
и 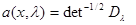 определяются следующими выражениями:
определяются следующими выражениями:
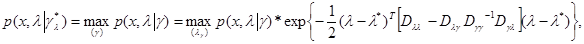 (6.5.15)
(6.5.15)
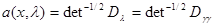 , (6.5.16)
, (6.5.16)
где 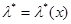 является решением уравнения (6.3.3), а матрицы
является решением уравнения (6.3.3), а матрицы 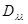 ,
, 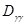 ,
, 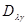 ,
, 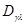 определяются выражениями (6.3.4) и зависят только от х (непосредственно и через
определяются выражениями (6.3.4) и зависят только от х (непосредственно и через 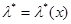 и
и 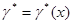 ,
, 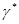 совместно с
совместно с 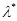 является решением уравнения (6.3.3)). С учетом (6.5.15), (6.5.16) выражение для апостериорного риска (6.5.8) принимает вид
является решением уравнения (6.3.3)). С учетом (6.5.15), (6.5.16) выражение для апостериорного риска (6.5.8) принимает вид
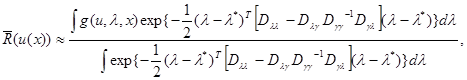 (6.5.17)
(6.5.17)
из которого следует, что решение u = u*(x) зависит от х посредством достаточной статистики 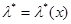 - оценки параметра
- оценки параметра  , определяемой из уравнения (6.3.3).
, определяемой из уравнения (6.3.3).
Если множество решений u имеет ту же структуру, что и множество  , и функция потерь g(u,
, и функция потерь g(u,  , х) является симметричной функцией разности u -
, х) является симметричной функцией разности u -  , то решение u*(х) просто совпадает с
, то решение u*(х) просто совпадает с  *(х), то есть получается точно таким же, как адаптивное байесово решение.
*(х), то есть получается точно таким же, как адаптивное байесово решение.
При произвольной структуре множества решений u оценка апостериорного риска (6.5.17), получающаяся с использованием принципа усреднения по неизвестным параметрам  среднего риска, отличается от оценки апостериорного риска (6.2.5), получающейся при адаптивном байесовом подходе с использованием оценки максимального правдоподобия
среднего риска, отличается от оценки апостериорного риска (6.2.5), получающейся при адаптивном байесовом подходе с использованием оценки максимального правдоподобия  * для параметров
* для параметров  , только за счет различия матриц
, только за счет различия матриц 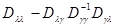 и
и 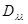 . Первая из них фигурирует в выражении (6.5.17), дающем оценку апостериорного риска при использовании принципа усреднения, а вторая - в выражениях типа (6.2.3), (6.3.5) при подстановке в них
. Первая из них фигурирует в выражении (6.5.17), дающем оценку апостериорного риска при использовании принципа усреднения, а вторая - в выражениях типа (6.2.3), (6.3.5) при подстановке в них  =
=  * в соответствии с принципами адаптивного байесова подхода.
* в соответствии с принципами адаптивного байесова подхода.
Таким образом, используемые в обоих случаях приближения для апостериорной плотности вероятности  , с помощью которых вычисляются оценки апостериорного риска и находятся минимизирующие этот риск решения, имеют одинаковый функциональный вид, одинаковое математическое ожидание
, с помощью которых вычисляются оценки апостериорного риска и находятся минимизирующие этот риск решения, имеют одинаковый функциональный вид, одинаковое математическое ожидание  * и несколько отличные матрицы вторых моментов. Естественно, что для всех задач (характеризуемых структурой множества решений U и видом функции потерь g(u,
* и несколько отличные матрицы вторых моментов. Естественно, что для всех задач (характеризуемых структурой множества решений U и видом функции потерь g(u,  , x)), в которых подобно задаче с функцией потерь, являющейся симметричной функцией разности u -
, x)), в которых подобно задаче с функцией потерь, являющейся симметричной функцией разности u -  , вид решения зависит только от апостериорного математического ожидания, принцип усреднения риска по
, вид решения зависит только от апостериорного математического ожидания, принцип усреднения риска по  дает точно такое же правило решения, как и адаптивный байесов подход. В тех задачах, в которых решение u*(х) зависит не только от апостериорного математического ожидания
дает точно такое же правило решения, как и адаптивный байесов подход. В тех задачах, в которых решение u*(х) зависит не только от апостериорного математического ожидания 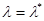 , оно может несколько отличаться от адаптивного байесова решения. Однако из-за асимптотической близости матриц
, оно может несколько отличаться от адаптивного байесова решения. Однако из-за асимптотической близости матриц 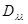 и
и 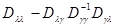 , имеющейся, как мы убедимся в дальнейшем, практически всегда, эти различия малосущественны, и во всех реальных случаях, когда совокупность неизвестных параметров
, имеющейся, как мы убедимся в дальнейшем, практически всегда, эти различия малосущественны, и во всех реальных случаях, когда совокупность неизвестных параметров  не зависит от
не зависит от  , правило решения, минимизирующее усредненный по неизвестным параметрам
, правило решения, минимизирующее усредненный по неизвестным параметрам  риск, совпадает с адаптивным байесовым правилом решения.
риск, совпадает с адаптивным байесовым правилом решения.
Дата добавления: 2018-05-10; просмотров: 1111;











