ПРИНЦИП МИНИМУМА УСРЕДНЕННОГО РИСКА

Рассмотренный в п. 4.3.4 принцип минимума усредненного риска заслуживает более детального обсуждения, поскольку сам по себе он является средством устранения априорной неопределенности при реше­нии задач синтеза, имеющим не меньшее значение, чем, например, ми­нимаксный подход. Проанализируем структуру правил решения, кото­рые могут быть найдены на его основе, и сравним их с адаптивными байесовыми правилами, полученными выше.

Применительно к случаю параметрической априорной Неопределен­ности принцип минимума усредненного риска выглядит особенно просто и заключается в выборе правила решения u(x) = u*(x) из условия минимума выражения

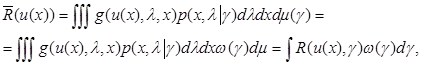(6.5.1)

где 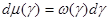( может содержать дельта-функции).

Как уже подчеркивалось в гл. 4, функция , характеризующая меру 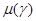, может иметь два истолкования. Она может быть не связана с каким-либо распределением вероятности параметров g (которое мо­жет и не существовать из-за невозможности вероятностной интерпрета­ции g), а характеризовать относительную значимость потерь при дан­ном значении у. В конкретных задачах часто имеются объективные и субъективные предпосылки для такой оценки степени значимости по­терь при разных значениях параметров g. При такой интерпретации не обязательно должна удовлетворять условию нормировки. Вто­рое истолкование связано с интерпретацией ее как плотности не­которого распределения вероятности параметров g, которое в действи­тельности существует, но может быть неизвестно.

Какой бы из способов истолкования мы ни приняли, естественно, что если функция задана, то это полностью снимает априорную неопределенность, поскольку выражение (6.5.1) для усредненного зна­чения среднего риска 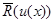формально соответствует обычной байесовой задаче, в которой совместное распределение вероятности х в g полностью известно и характеризуется плотностью (4.3.9):

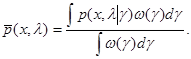(6.5.2)

Само оптимальное (минимизирующее усредненный риск) правило ре­шения u*(х) находится минимизацией следующего выражения

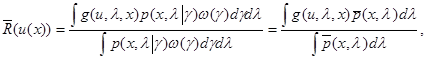(6.5.3)

которое является формальным представлением для апостериорного риска в случае, когда распределение вероятности х и задается (6.5.2).

Если функция действительно известна, то никакой проблемы нет; остается только чисто техническая процедура нахождения значе­ния u = u*(x), минимизирующего (6.5.3) при каждом данном х. Соот­ветствующее отображение u(x) = u*(x), определенное для всех значе­ний х, и задает оптимальное правило решения. При этом исходная априорная неопределенность в статистическом описании х и , не по­зволяющая точно задать их совместное распределение вероятности, естественно, не имеет принципиального значения и не является сущест­венной с точки зрения решения задачи синтеза.

На самом деле проблема возникает, когда неизвестна, и апри­орная неопределенность является существенной. Покажем, что если при этом ввести несущественные предположения о характере измене­ния , то можно получить новое решение задачи синтеза в условиях априорной неопределенности, причем полученное правило решения будет точно или с высокой степенью приближения совпадать с найден­ным выше адаптивным байесовым правилом.

Итак, предположим, что является относительно медленно меняющейся функцией в том смысле, что в окрестности любой точки g = g_o эта функция меняется существенно медленнее, чем функция 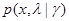при любых фиксированных значениях х и . Конкретные тре­бования на допустимую скорость изменения уточним несколько ниже. Кроме того, для сокращения записи предположим, что нор­мирована на единицу. Из выражения (6.5.3) для апостериорного риска, минимизацией которого находится правило решения, видно, что это предположение не имеет никакого значения, поскольку входит в числитель и знаменатель этого выражения.

Идея излагаемого далее способа нахождения правила решения основана на использовании асимптотического метода интегрирования Лапласа при вычислении интеграла (6.5.2) для нахождения прибли­женного выражения плотности вероятности .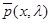

Обозначим через 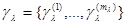ту часть параметров , от ко­торой действительно зависит функция 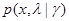при данном (в общем случае плотность вероятности 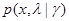при фиксированном значении , может зависеть только от части параметров , а не от всех этих пара­метров). Обозначим также через 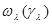функцию, которая получается из интегрированием по тем из параметров , которые не вошли в со­вокупность 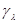. Пусть также при любом величины 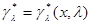(век­торы размерности 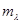) определяются из уравнения

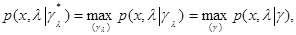(6.5.4)

то есть максимизируют функцию 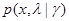при данных значениях х и и являются условными оценками максимального правдоподобия пара­метров при данном . Естественно, что эти величины, вообще говоря, отличаются от безусловных оценок максимального правдоподобия 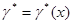, определяемых уравнением (6.2.15). Пусть также функция 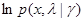дважды дифференцируема по при всех х и . Тогда, при­меняя асимптотический метод интегрирования Лапласа, основанный на аппроксимации функции 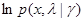квадратичным разложением в окрестности точки 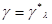, получаем приближенное выражение для {6.5.2) (с учетом предположения о нормировке функции )

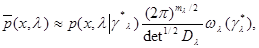(6.5.5)

где 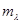- общее число компонент параметра ;

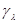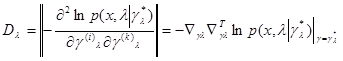(6.5.6)

- матрица вторых производных функции 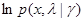в точке .

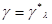Приближение (6.5.5) справедливо при выполнении следующих условий, которые являются обычными условиями применимости асимптотического метода интегрирования Лапласа:

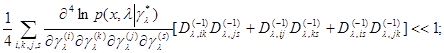
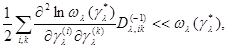(6.5.7)

где 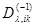- элемент матрицы 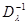, обратной матрице .

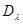При выполнении этих условий имеем следующее приближение для апостериорного риска (6.5.3):

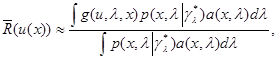(6.5.8)

где функция 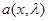определяется выражением

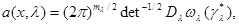(6.5.9)

и обычное уравнение для нахождения оптимального правила решения

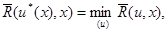(6.5.10)

в котором функция 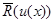определяется точным (6.5.3) или прибли­женным (6.5.8) выражением.

Найденное таким образом правило решения, очевидно, удовлетво­ряет основному принципу адаптивного байесова подхода - оно соот­ветствует минимуму оценочного значения апостериорного риска, при­чем в качестве оценки используется приближенное выражение 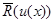из (6.5.8). Отличие от использованной ранее оценки апостериорного риска (6.2.5) заключается в том, что выражение (6.5.8) допускает при­менение различных оценок параметров при разных значениях , в то время как в (6.2.5) и последующих выражениях оценка неизвестного значения производится в целом, для всех значений .

Остановимся на одной важной особенности правила решения u*(х). Возьмем какое-либо правило решения u(х) и рассмотрим отклонение среднего риска этого правила от минимального байесова риска для оптимального правила решения u₀(х, ) с известным , то есть величину

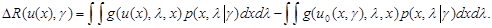(6.5.11)

Произведем усреднение этой разности с весовой функцией , то есть найдем средневзвешенное отклонение

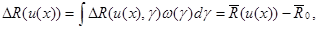(6.5.12)

где 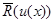- усредненный риск (6.5.1), а 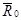- средневзвешенное зна­чение минимального байесова риска.

Если теперь выбрать правило решения u(х) так, чтобы минимизи­ровать средневзвешенное отклонение 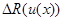, то в силу того, что 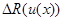отличается от 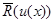на несущественную константу, это правило решения будет точно таким же, как правило решения u*(х), обеспечивающее минимум усредненного риска.

Таким образом, получаем важное свойство правила решения (6.5.10) - оно обеспечивает наилучшее в среднем с весом при­ближение к абсолютно оптимальному байесову правилу при отсутствии априорной неопределенности (известном значении ). Напомним, что полученное в § 6.2 адаптивное байесово правило u(x) = u₀(x, *) также является наилучшим приближением к оптимальному байесову прави­лу, удовлетворяя другому критерию близости - критерию минимума максимального отклонения, а не минимума средневзвешенного откло­нения.

Доказанное свойство правила решения u*(х) из (6.5.10) является основой для еще одного истолкования функции . А именно, послед­няя может интерпретироваться как весовая функция, используемая при вычислении среднего отклонения риска некоторого произвольного пра­вила решения от минимального байесова риска и характеризующая зна­чимость отклонений при разных значениях с точки зрения последую­щего выбора наилучшего приближенного правила решения. Эта интер­претация до крайности упрощает проблему априорной неопределенно­сти и лишает ее мистических покровов.

Действительно, если с самого начала четко представить себе, что при отсутствии полного статистического описания невозможно полу­чить строго оптимальное байесово правило решения и самое большее, что можно сделать, это найти наилучшее в том или ином смысле при­ближение к этому решению, если, кроме того, принять в качестве есте­ственного критерия близости величину средневзвешенного отклонения среднего риска от минимального байесова и задать какую-либо подхо­дящую весовую функцию . Для вычисления этого отклонения, то задача синтеза строго и формально решается до конца. При этом функ­цию можно формально использовать так, как если бы она была (с учетом соответствующей нормировки, возможно, даже на расходя­щуюся величину) плотностью некоторого априорного распределения вероятности, заданного на множестве значений параметров , хотя по существу эта функция совсем не обязана быть такой плотностью, а па­раметры могут и не иметь вероятностной интерпретации.

Нужно подчеркнуть, что если с формальной точки зрения интер­претация безразлична, то по существу для реальных возможно­стей задания функции разные ее интерпретации глубоко различ­ны. На самом деле, требуется серьезное пренебрежение к уровню своей неосведомленности (в случае, когда все или часть параметров не имеют ясного вероятностного истолкования), чтобы задать какое-то априорное распределение вероятности для параметров с плотностью <o(y). Имеется значительно больше оснований задать функцию , характеризующую значимость потерь, при разных значениях . И, ве­роятно, даже не нужно особенно задумываться об основаниях и дета­лях выбора , если мы задаем ее как весовую функцию для расчета средневзвешенного отклонения риска приближенно оптимального пра­вила решения от абсолютно оптимального байесова правила. В этом случае выбор - это целиком дело разработчика алгоритма обра­ботки информации, а основанием для такого выбора могут быть чисто субъективные соображения.

Нужно отметить также, что использование того или иного критерия приближения (минимума максимального отклонения, приводящего к адаптивному байесову правилу решения u(x) = u₀(x, *), или мини­мума средневзвешенного отклонения, приводящего к правилу решения u*(x) из (6.5.10)) в общем определяется некоторыми посторонними и подчас субъективными соображениями. Стоит все-таки только подчерк­нуть, что первый критерий гарантирует точность приближения при лю­бом конкретном значении не хуже определенного уровня и поэтому кажется более предпочтительным при единичном использовании соот­ветствующего правила решения либо при многократном использовании этого правила, когда будет встречаться одно и то же или немногие из возможных значений . Второй критерий обеспечивает наилучшее при­ближение в среднем и кажется более предпочтительным, если синтези­рованный алгоритм обработки информации (правило решения) будет применяться многократно и при разных повторениях будут встречаться многие из возможных значений .