Минимаксиминный принцип

Адаптивное байесово правило решения (при всех g) лучше (не ху­же) минимаксиминного правила решения. Это следует из того, что принцип выбора обоих видов правил одинаков - берется байесово правило решения, определенное с точностью до параметра g, подбирается наилучшее из наихудших значений g и подставляется в байесово пра­вило решения - за исключением одной весьма существенной детали: в минимаксиминном правиле решения наилучшее значение выбирается из заданного числового множества его значений и не зависит от данных наблюдения х; в адаптивном правиле это значение выбирается из зна­чительно более обширного множества значений всех g(х), в результате чего наилучшее значение подбирается для каждого х. Поскольку мно­жество всех функций g(x) отображающих х в g, содержит в качестве подмножества и функции вида g(x) = g = const при всех x используемые при выборе минимаксиминного правила решения, то ясно, что послед­нее не может быть лучше адаптивного правила ни при каких истинных значениях g.

Принцип минимакса

В общем случае адаптивное байесово и минимаксное решающие правила находятся в обычном соотношении, обсуждавшемся в гл. 4. Максимальное (по g) значение среднего риска для адаптивного байесова правила не меньше, чем величина минимаксного риска, однако при других значениях g средний риск адаптивного байесова правила может быть меньше и даже существенно меньше минимаксного риска. В этой связи особый интерес представляет выявление случаев, когда макси­мальный средний риск адаптивного байесова правила решения не пре­вышает величины минимаксного риска. В таких случаях адаптивное правило равномерно (то есть при всех значениях g) не хуже минимакс­ного правила, а при некоторых (или даже почти всех) значениях g мо­жет оказаться лучше минимаксного.

Один из подобных примеров уже был рассмотрен в § 5.6, где мы нашли совокупность решающих правил (5.6.11); максимальная вели­чина риска достигается при единственном значении неизвестного пара­метра функции правдоподобия 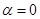и точно равна минимаксному зна­чению, а при всех 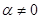риск меньше минимаксного. Покажем, что пра­вило решения (5.6.11) является адаптивным байесовым правилом и может быть найдено с помощью адаптивного байесова подхода. Дей­ствительно, в общем случае байесово правило решения для двухальтернативной задачи имеет вид

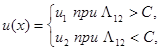
где для случая § 5.6 отношение правдоподобия

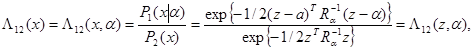
z = z(x) - достаточная статистика, линейно зависящая от х и опреде­ляемая выражением (5.6.7). Это отношение правдоподобия зависит от неизвестного параметра 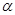, который при адаптивном байесовом подходе следует заменить оценкой максимального правдоподобия 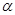* = *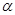(х).

Последняя согласно (6.2.15) определяется из уравнения правдоподо­бия 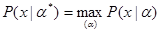, решение которого с учетом выражений имеет вид 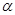* = z.

После подстановки этой оценки в отношение правдоподобия мы. приходим к правилу принятия решения

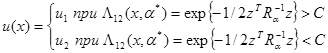
или эквивалентному ему правилу решения (5.6.11).

Можно привести и другие примеры, когда максимальный средний риск адаптивного байесова правила решения не превышает минимакс­ного риска. Это имеет место, в частности, для всего класса задач, в ко­торых средний риск оптимального байесова правила решения при из­вестном значении g не зависит от этого значения g, хотя само оптимальное правило явно зависит от g и равномерно наилучшего пра­вила решения не существует. Примеры таких задач довольно много­численны. Доказательство высказанного утверждения заключается в следующем. Адаптивное правило решения при выборе оценки 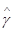(х) в соответствии с требованием (6.2.12) удовлетворяет принципу минимакса для отклонения 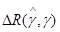среднего риска от среднего риска опти­мального байесова правила решения. Поскольку последний не зависит от g, то адаптивное байесово правило решения одновременно удовле­творяет принципу минимакса и для самой величины среднего риска 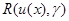, то есть для этого правила 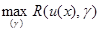не превосходит величины минимаксного риска. Так же как утверждение п. 6.4.4, это утверждение, строго говоря, справедливо при подстановке в правило решения (6.2.6) оценки 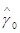(x), удовлетворяющей требованию (6.2.12), и может оказаться неточным при использовании оценки максимального правдоподобия g*(x), если последняя заметно отличается от 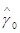(x).

Интересно было бы найти достаточно общие условия, при которых максимум риска адаптивного байесова правила решения не больше минимаксного риска. Однако, по-видимому, такая задача не проще, а может быть и сложнее, чем задача отыскания минимаксных правил решения в общем случае, и еще ждет своего решения.