Классические B-деревья

Механизм классических B-деревьев был предложен в 1970 г. Бэйером и Маккрейтом. B-дерево порядка n представляет собой совокупность иерархически связанных страниц внешней памяти (каждая вершина дерева - страница), обладающая следующими свойствами:

1.Каждая страница содержит не более 2*n элементов (записей с ключом).

2.Каждая страница, кроме корневой, содержит не менее n элементов.

3.Если внутренняя (не листовая) вершина B-дерева содержит m ключей, то у нее имеется m+1 страниц-потомков.

4.Все листовые страницы находятся на одном уровне.

Количество обращений к диску при этом для поиска любой записи одинаково и равно количеству уровней в построенном дереве. Такие деревья называются сбалансированными (balanced) именно потому, что путь от корня до любого листа в этом древе одинаков. Именно термин "сбалансированное" от английского "balanced" - "сбалансированный, взвешенный" и дал название данному методу организации данных.

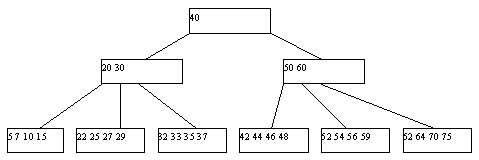
Рис. 1. Классическое B-дерево порядка 2

Поиск в B-дереве производится очевидным образом. Предположим, что происходит поиск ключа K. В основную память считывается корневая страница B-дерева. Предположим, что она содержит ключи k1, k2, ..., km и ссылки на страницы p0, p1, ..., pm. В ней последовательно (или с помощью какого-либо другого метода поиска в основной памяти) ищется ключ K. Если он обнаруживается, поиск завершен. Иначе возможны три ситуации:

1.Если в считанной странице обнаруживается пара ключей ki и k(i+1) такая, что ki < K < k(i+1), то поиск продолжается на странице pi.

2.Если обнаруживается, что K > km, то поиск продолжается на странице pm.

3.Если обнаруживается, что K < k1, то поиск продолжается на странице p0.

Для внутренних страниц поиск продолжается аналогичным образом, пока либо не будет найден ключ K, либо мы не дойдем до листовой страницы. Если ключ не находится и в листовой странице, значит ключ K в B-дереве отсутствует.

Включение нового ключа K в B-дерево выполняется следующим образом. По описанным раньше правилам производится поиск ключа K. Поскольку этот ключ в дереве отсутствует, найти его не удастся, и поиск закончится в некоторой листовой странице A. Далее возможны два случая. Если A содержит менее 2*n ключей, то ключ K просто помещается на свое место, определяемое порядком сортировки ключей в странице A. Если же страница A уже заполнена, то работает процедура расщепления. Заводится новая страница C. Ключи из страницы A (берутся 2*n-1 ключей) + ключ K поровну распределяются между A и C, а средний ключ вместе со ссылкой на страницу C переносится в непосредственно родительскую страницу B. Конечно, страница B может оказаться переполненной, рекурсивно сработает процедура расщепления и т.д., вообще говоря, до корня дерева. Если расщепляется корень, то образуется новая корневая вершина, и высота дерева увеличивается на единицу. Одношаговое включение ключа с расщеплением страницы показано на рисунке 2.

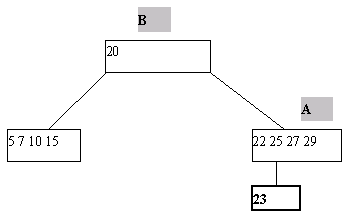
(a) Попытка вставить ключ 23 в уже заполненную страницу

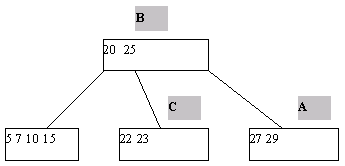
(b) Выполнение включения ключа 22 путем расщепления страницы A
Рис.2. Пример включения ключа в B-дерево

Процедура исключения ключа из классического B-дерева более сложна. Приходится различать два случая - удаление ключа из листовой страницы и удаления ключа из внутренней страницы B-дерева. В первом случае удаление производится просто: ключ просто исключается из списка ключей. При удалении ключа во втором случае для сохранения корректной структуры B-дерева его необходимо заменить на минимальный ключ листовой страницы, к которой ведет последовательность ссылок, начиная от правой ссылки от ключа K (это минимальный содержащийся в дереве ключ, значение которого больше значения K). Тем самым, этот ключ будет изъят из листовой страницы (рисунок 3).

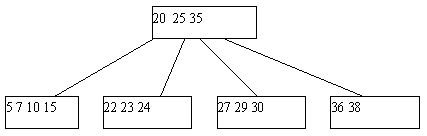
(a) Начальный вид B-дерева

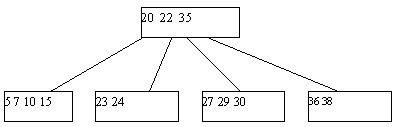
(b) B-дерево после удаления ключа 25
Рис. 3. Пример исключения ключа из B-дерева

Поскольку в любом случае в одной из листовых страниц число ключей уменьшается на единицу, может нарушиться то требование, что любая, кроме корневой, страница B-дерева должна содержать не меньше n ключей. Если это действительно случается, начинает работать процедура переливания ключей. Берется одна из соседних листовых страниц (с общей страницей-предком); ключи, содержащиеся в этих страницах, а также средний ключ страницы-предка поровну распределяются между листовыми страницами, и новый средний ключ заменяет тот, который был заимствован у страницы-предка (рисунок 4).

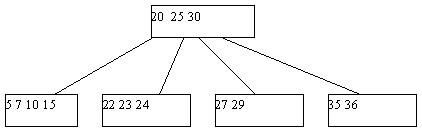
Рис. 4. Результат удаления ключа 38 из B-дерева с рисунка 5.3

Может оказаться, что ни одна из соседних страниц непригодна для переливания, поскольку содержат по n ключей. Тогда выполняется процедура слияния соседних листовых страниц. К 2*n-1 ключам соседних листовых страниц добавляется средний ключ из страницы-предка (из страницы-предка он изымается), и все эти ключи формируют новое содержимое исходной листовой страницы. Поскольку в странице-предке число ключей уменьшилось на единицу, может оказаться, что число элементов в ней стало меньше n, и тогда на этом уровне выполняется процедура переливания, а возможно, и слияния. Так может продолжаться до внутренних страниц, находящихся непосредственно под корнем B-дерева. Если таких страниц всего две, и они сливаются, то единственная общая страница образует новый корень. Высота дерева уменьшается на единицу, но по-прежнему длина пути до любого листа одна и та же. Пример удаления ключа со слиянием листовых страниц показан на рисунке 5.

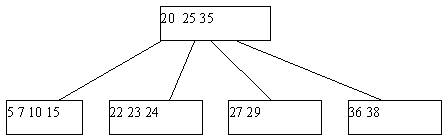
(a) Начальный вид B-дерева

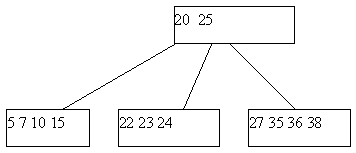
(b) B-дерево после удаления ключа 29
Рис. 5. Пример удаления ключа из B-дерева со слиянием листовых страниц

B+-деревья

Схема организации классических B-деревьев проста, но не очень хороша для практического использования. Прежде всего это связано с тем, что в большинстве практических применений необходимо хранить во внешней памяти не только ключи, но и записи. Поскольку в B-дереве элементы располагаются и во внутренних, и в листовых страницах, а размер записи может быть достаточно большим, внутренние страницы не могут содержать слишком много элементов, по причине дерево может быть довольно глубоким. Поэтому для доступа к ключам и записям, находящимся на нижних уровнях дерева, может потребоваться много обменов с внешней памятью. Во-вторых, на практике часто встречается потребность хранения и поиска ключей и записей переменного размера. Поэтому тот критерий, что в каждой странице B-дерева содержится не меньше n и не больше 2*n ключей, становится неприменимым.

Широкое практическое применение получила модификация механизма B-деревьев, которую принято называть B+-деревьями. Эти деревья похожи на обычные B-деревья. Они тоже сильно ветвистые, и длина пути от корня к любой листовой странице одна и та же. Но структура внутренних и листовых страниц различна. Внутренние страницы устроены так же, как у B-дерева, но в них хранятся только ключи (без записей) и ссылки на страницы-потомки. В листовых страницах хранятся все ключи, содержащиеся в дереве, вместе с записями, причем этот список упорядочен по возрастанию значения ключа (рисунок 6).

Поиск ключа всегда доходит до листовой страницы. Аналогично операции включения и исключения тоже начинаются с листовой страницы. Для применения переливания, расщепления и слияния используются критерии, основанные на уровне заполненности соответствующей страницы. Для более экономного и сбалансированного использования внешней памяти при реализации B+-деревьев иногда используют технику слияния трех соседних страниц в две и расщепления двух соседних страниц в три. Хотя B+-деревья хранят избыточную информацию (один ключ может храниться в двух страницах), они, очевидно, обладают меньшей глубиной, чем классические B-деревья, а для поиска любого ключа требуется одно и то же число обменов с внешней памятью.

(a) Структура внутренней страницы B+-дерева

(b) Структура листовой страницы B+-дерева
Рис. 5.6. Структуры страниц B+-дерева

Дополнительной полезной оптимизацией B+-деревьев является связывание листовых страниц в одно- или двунаправленный список. Это позволяет просматривать списки записей для заданного диапазона значений ключей с лишь одним прохождением дерева от корня к листу.