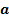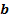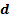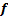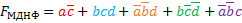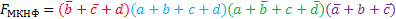Диаграмма Вейча для функции от 2 переменных

МДНФ:

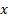
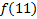
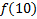
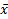
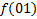
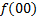
МКНФ:

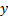
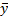
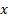
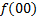
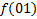
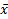
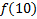
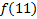
Диаграмма Вейча для функции от 3 переменных

МДНФ:

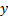
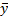
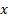
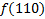
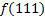
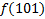
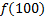
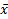
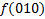
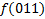
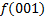
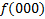
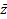
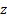
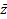
МКНФ:

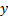
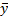
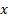
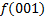
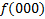
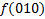
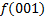
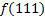
Диаграмма Вейча для функции от 4 переменных

МДНФ:

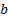
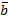
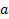
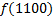
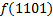
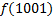
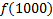
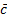
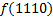
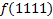
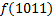
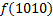
МКНФ:

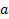
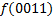
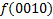
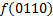
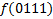
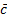
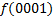
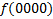
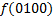
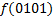
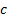
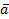
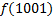
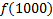
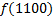
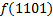
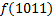
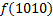
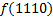
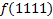
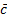
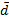
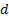
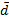
Наборы значений функции для МКНФ по отношению к МДНФ инвертируются.

Пусть дана таблица истинности логической функции:

1. Составим для данной функции диаграмму Вейча (МДНФ) и выделим интервалы:

По данной диаграмме составим формулу:

2. Составим для данной функции диаграмму Вейча (МКНФ) и выделим интервалы:

По данной диаграмме составим формулу:

Диаграмма Вейча для функции от 5 переменных

МДНФ:

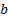
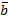
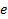
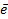
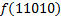
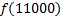
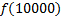
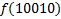
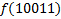
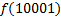
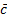
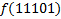
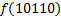
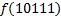
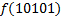
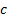
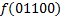
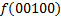
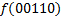
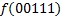
МКНФ:

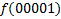
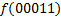
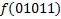
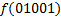
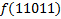
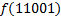
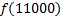
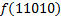
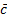
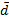
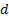
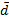
Дата добавления: 2017-11-21; просмотров: 1957;