Множество логических функций от двух переменных

Аргументы

Логические функции от двух переменных

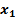
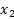
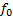
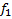
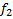
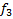
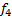
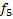
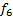
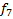
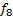
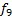
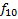
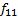
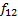
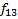
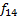
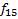
Заметим, что уникальных функций всего 8. Каждой соответствует инверсированная пара, иными словами:

, .

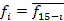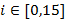F₁(x₁,x₂) – конъюнкция

Элементарная логическая функция (логическое произведение, И). Конъюнкция истинна тогда и только тогда, когда все ее аргументы истинны.

F₇(x₁,x₂) – дизъюнкция

Элементарная логическая функция (логическое сложение, ИЛИ). Дизъюнкция истинна, если хотя бы один ее аргумент истинен.

F₆(x₁,x₂) – строгая дизъюнкция

Сложение по модулю 2, исключающее ИЛИ. Обозначение: ⊕.

F₈(x₁,x₂) – Элемент Вебба (стрелка Пирса)

Реализует функцию ИЛИ-НЕ. Является базисным элементом, т.е. только через ИЛИ-НЕ можно реализовать любую логическую функцию. Возвращает истину, когда все аргументы ложны. Обозначение: ↑.

F₁₄(x₁,x₂) – Функция штрих Шеффера

Реализует функцию И-НЕ. Является базисным элементом, т.е. только через И-НЕ можно реализовать любую функцию. Обозначение: |.