Диаграмма Вейча (карта Карно)

Графический способ минимизации логических функций. Работает на основе операций склеивания и поглощения. Представляет собой особым образом переупорядоченную таблицу истинности.

Операция склеивания осуществляется между двумя совершенными конъюнктами (дизъюнктами), у которых совпадают все литералы, кроме одного. По правилам склеивания совпадающие литералы выносятся за скобки, а оставшиеся подвергнуть склейке.

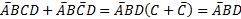
В диаграмме Вейча ячейки таблицы истинности сгруппированы таким образом, что переход из одной ячейки в другую по вертикали или горизонтали связан с изменением значения только одной переменной. В результате этого наборы, между которыми возможно склеивание, получаются сгруппированными вместе и их легко заметить. Метод Вейча подходит для минимизации функций до 7 переменных. При большем количестве теряются достоинства метода.

Интервал логической функции от 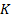переменных – это такое множество наборов значений переменных, что:

· Значение функции на этом множестве постоянно;

· Мощность (величина, размер интервала) этого множества равна , ;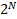

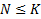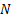· является количеством переменных, которые упрощаются на этом множестве, а оставшихся ( 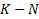) переменных достаточно для описания логической функции на данном множестве;

· Если 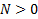, то каждый следующий набор отличается от предыдущего значением только одной переменной.

Типы интервалов

Интервал размера 1

Вырожденный случай. Упрощения не происходит. Интервал может встречаться на любых диаграммах.

Интервал размера 2

Упрощается одна переменная. Интервалы могут встречаться на любых диаграммах.

Интервал размера 4

Упрощается 2 переменных. Некоторые интервалы встречаются, начиная с диаграммы Вейча для функции от 3 переменных.