Явнополюсный генератор

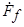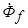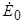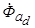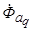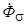При составлении уравнения напряжений ненасыщенного явнополюсного генератора можно также использовать метод наложения. Здесь МДС обмотки возбуждения , как и в случае неявнополюсного генератора, создает поток , который, сцепляясь с обмоткой статора, наводит в ней ЭДС . Магнитный поток обмотки статора представим в виде суммы трех составляющих - , и . Каждый из этих потоков, сцепляясь с обмоткой статора, наводит в ней ЭДС 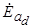, 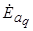и 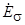соответственно. Напряжение генератора в этом случае будет равно геометрической сумме этих ЭДС минус падение напряжения на активном сопротивлении:

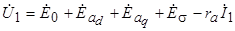. (5.8)

Модуль ЭДС 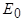определяется по спрямленной характеристике холостого хода (рис.5.6) при заданном значении тока возбуждения 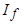. Для определения ЭДС реакции якоря 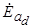и 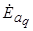разложим ток статора 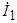на продольную 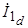и поперечную 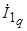составляющие:

,

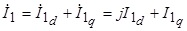где ; .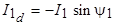

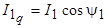Току 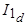соответствует МДС 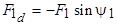, определяющая поток продольной реакции якоря, а току 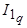соответствует МДС 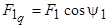, определяющая поток поперечной реакции якоря. Поэтому выражения для ЭДС 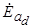и 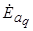можно представить в виде

;

,

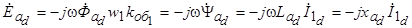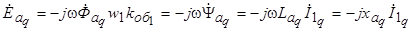где 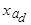- индуктивное сопротивление реакции якоря по продольной оси; 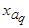- индуктивное сопротивление реакции якоря по поперечной оси.

ЭДС рассеяния определяется полным током статора

.

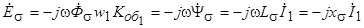Выразив ЭДС 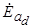, 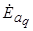и 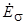через соответствующие индуктивные сопротивления и токи, преобразуем уравнение (5.8) к виду

.

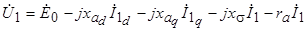Принимая во внимание, что 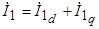, получим

,

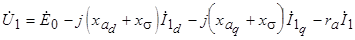или

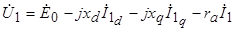, (5.9)

где 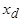- полное индуктивное сопротивление якоря по продольной оси; 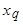- полное индуктивное сопротивление якоря по поперечной оси.

Уравнению (5.9) соответствуют векторные диаграммы для активно-индуктивной (рис. 5.13, а) и активно-емкостной (рис. 5.13, б) нагрузки.

Так же, как и в неявнополюсном генераторе, напряжение явнополюсного генератора 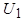снижается с увеличением активно-индуктивной нагрузки и растет при увеличении активно-емкостной нагрузки. Формально уравнение (5.9) можно свести к уравнению неявнополюсной машины, заменив в нем ток 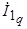на :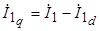

,

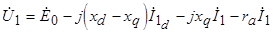или

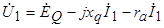, (5.10)

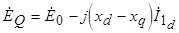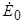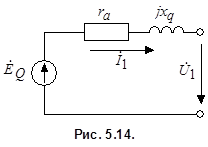
где - эквивалентная ЭДС явнополюсного генератора. Замена ЭДС на 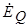позволяет воспользоваться простой схемой замещения явнополюсного синхронного генератора (рис. 5.14) при аналитических расчетах его режимов работы.

Внутреннее сопротивление явнополюсного генератора в этом случае определяется величиной

.

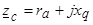На рис. 5.15 приведена векторная диаграмма, построенная по уравнению (5.10) для активно-индуктивной нагрузки. При упрощенных расчетах ЭДС 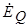принимают постоянной, пренебрегая ее изменением при изменении тока .

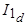Параметры современных синхронных генераторов явнополюсного исполнения в относительных единицах имеют следующие значения:

;

;

;

.

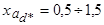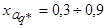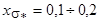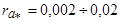5.6. Уравнения напряжений и векторные диаграммы
синхронного генератора с учетом насыщения