Производные функций, заданных неявно и параметрически.

Пусть функции х = j(t) и у = y(t) определены и дифференцируемы на некотором множестве Т и пусть j(t) имеет дифференцируемую обратную функцию t = j^–1(x) . Тогда функция у = y(j^–1(x)) есть сложная функция, которая может быть задана параметрически 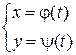, tÎ Т. Найдем производную этой функции. Используя правила дифференцирования сложной и обратной функций, имеем

у¢_х = (y(j^–1(x)))¢ = ,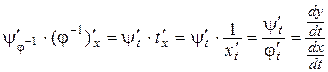

т.е. производная функции 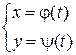равна

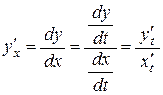. (2)

Например, для функции 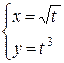, используя формулу (2), получим

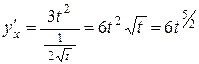
Если же записать функцию у как функцию от х: 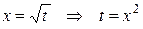Þ у = х⁶, то получим у¢ = 6х⁵ = 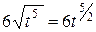– тот же результат.

Найдем вторую производную функции 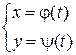, предполагая, что она существует. Первую производную у¢_х этой функции можно задать параметрически уравнениями 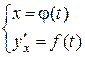. Применяя к этой функции правило (2), находим

.

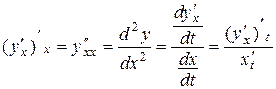Аналогично можно найти третью производную

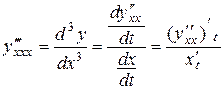, и т.д.

Рассмотрим неявно заданную функцию у переменной х: F(x, y) = 0

Правило дифференцирования неявной функции таково:

1) Продифференцировать обе части равенства F(x, y) = 0 по х, пользуясь основными правилами и формулами дифференцирования, но помня при этом, что у есть функция от х: у = у(х) с неизвестной производной (т.е. везде, где происходит дифференцирование у, обязательно умножать на у¢ как при дифференцировании сложной функции).

2) Из полученного равенства выразить у¢ через х и у.

Пример: Найдем производную функции у, заданной неявно уравнением

х² + 3ху + у³ = 5.

Действуем по изложенному правилу:

(х² + 3ху + у³)¢ = (5)¢, 2х + 3(х¢у + ху¢) + 3у²у¢ = 0,

2х + 3у + 3ху¢ + 3у²у¢ = 0, 3ху¢ + 3у²у¢ = –2х – 3у,

.

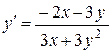Заметим, что производная неявной функции обычно также есть функция неявная.

4. Дифференциал функции, его приложения.

Линеаризация функции.

Согласно определению 4.2, функция у = f(x) называется дифференцируемой в точке х₀, если ее приращение Dу в этой точке представимо в виде

Dу = А.Dх + о(Dх),

где А – константа, причем из теоремы 4.2 следует, что А = f ¢(x₀). Таким образом, приращение дифференцируемой функции может быть представлено в виде суммы двух слагаемых, одно из которых – f ¢(x₀).Dх – линейно относительно приращения Dх (точнее, пропорционально ему), а другое – о(Dх) – есть бесконечно малая более высокого порядка, чем Dх. При Dх ® 0 бесконечно малые Dу и f ¢(x₀).Dх эквивалентны. Действительно

= .

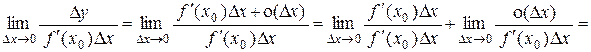
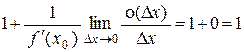Следовательно, основные свойства суммы f ¢(x₀).Dх + о(Dх) определяются свойствами первого слагаемого и эквивалентны свойствам самого приращения функции. Поэтому этому слагаемому в математике отводят особое место и называют его дифференциалом.

Определение 4.4.

Часть приращения функции у = f(x), линейная относительно приращения аргумента, называется дифференциалом этой функции и обозначается dy.

Таким образом, dy = f ¢(x₀).Dх.

Дифференциал функции у = f(x) обозначают также df(x), df. Дифференциал зависит от точки х₀ и от величины приращения Dх. При фиксированном Dх имеем dy = f ¢(x).Dх – функция переменной х. Рассмотрим функцию у = х, используя равенство df(x) = f ¢(x).Dх, получаем dx = Dx, т.е. дифференциал независимой переменной равен ее приращению. Учитывая это свойство, принято записывать

dy = f ¢(x).dх. (3)

Эту формулу обычно используют для вычисления дифференциала функции в произвольной точке, в которой эта функция дифференцируема. Например,

dsin(3x+1) = 3cos(3x+1)dx.

Кроме того, в силу формулы (1), непосредственно из правил вычисления производной вытекают правила нахождения дифференциалов:

dc = 0, c – const d(u ± v) = du ± dv

d(uv) = vdu + udv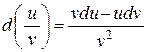

Докажите эти формулы самостоятельно.

Из правила дифференцирования сложной функции следует замечательное свойство дифференциала – свойство инвариантности (неизменности) дифференциала: пусть у = f(j(x)), обозначим и = j(х); тогда

,

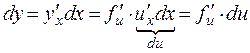значит, форма дифференциала не зависит от того, является ли аргумент независимой переменной или функцией другого аргумента.

Из формулы (3) следует также, что 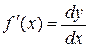, т.е. используемое нами выражение 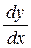можно понимать не только как обозначение производной, но и как отношение дифференциалов зависимой и независимой переменных.

Определим геометрический смысл дифференциала. Рассмотрим график функции у = f(x). Возьмем на этом графике точку А(х₀ ; f(x₀)) и проведем в ней касательную к графику функции (рис. 1).

Имеем dy = f ¢(x₀).Dх. Учитывая геометрический смысл производной, получаем 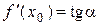, откуда dy = tga.Dх.

Таким образом, dy = CB, т.е. приращению касательной в точке х₀. Итак, с геометрической точки зрения, дифференциал функции характери­зует приращение ординаты касательной к графику функции в заданной точке.

Итак, имеем Dу = dy +o(Dx), откуда Dу » dy, причем, это равенство тем точнее, чем меньше Dх. Так как Dу = f(x₀ + Dx) – f(x₀), а dy = f ¢(x₀)Dx, то

f(x₀ + Dx) – f(x₀) » f ¢(x₀)Dx,

откуда f(x₀ + Dx) » f(x₀) + f ¢(x₀)Dx.

Положим х = х₀ + Dх, тогда получим

f(x) » f(x₀) + f ¢(x₀)Dx , (4)

эту формулу можно использовать для приближенного вычисления значения функции в некоторой точке х по известному (или легко вычисляемому) значению функции и ее производной в соседней точке х₀.

Заменим в формуле (4) Dх = х – х₀, получим

f(x) » f(x₀) + f ¢(x₀)(х – х₀),

или f(x) » f(x₀) + f ¢(x₀).х – f ¢(x₀).х₀. Обозначим f(x₀) – f ¢(x₀).х₀ = В – const, , а так как f ¢(x₀).х = А.х, то получим f(x) » А.х + В. Значит, формула (4) показывает, что вблизи точки х₀ функция f(x) может быть приближенно заменена линейной функцией. Поэтому формулу

f(x) » f(x₀) + f ¢(x₀)(х – х₀)

называют формулой линеаризации функции в окрестности точки х₀.

Замена функции приближенно равной ей линейной функцией называется линеаризацией функции или линейной аппроксимацией.

Например, линеаризуем функцию f(x) = ln( 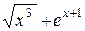) в окрестности точки х₀ = 0. Вычислим:

f(0) = ln e = 1, f ¢(0) = 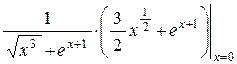= 1.

Тогда вблизи точки 0 выполняется равенство f(x) » 1+ х.

Геометрически линеаризация функции означает, что в окрестности точки графика с абсциссой х₀ линия графика заменяется отрезком прямой, которая, очевидно, является касательной к графику функции в соответствующей точке. Уравнение этой касательной имеет вид

у = f(x₀) + f ¢(x₀)(х – х₀).

Прямая, проходящая через точку (х₀, f(x₀))перпендикулярно касательной, называется нормалью к линии у = f(x) в этой точке. Уравнение нормали имеет вид

у = f(x₀) – 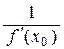(х – х₀).

Аналогично тому, как были определены производные высших порядков, можно ввести понятие дифференциалов высших порядков:

d⁽ⁿ⁾y = d(d^(n–1)y)

Отметим формулы, с помощью которых эти дифференциалы можно вычислять:

дифференциал второго порядка d²y = f¢¢ (x)dx², где dx² = (dx)²;

дифференциал третьего порядка d³y = f¢¢¢ (x)dx³, и т.д.

Заметим, что дифференциалы высших порядков свойством инвариантности не обладают.