Пересечение многогранника проецирующей плоскостью
Сечением многогранника плоскостью является многоугольник, вершинами которого служат точки пересечения ребер многогранника и секущей плоскости.
Построение сечения сводится к многократному решению задачи на пересечение прямой (ребра) с плоскостью или двух плоскостей. Первое решение проще, поэтому для нахождения сечений многогранника чаще используют его.
Пример 5. Построить сечение поверхности пирамиды SАВС наклонной плоскостью Б и определить натуру сечения (рисунок 9-1).
При решении этой задачи нужно использовать вырожденный вид секущей плоскости Б. В этом случае задача сводится к построению точки пересечения прямой общего положения и плоскости частного положения.
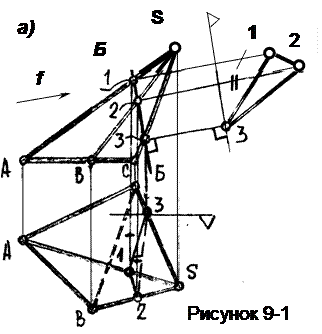 Сечение на виде спереди имеет вырожденный вид и совпадает с изображением плоскости Б. Точки 1,2,3, являются точками пересечения ребер пирамиды с плоскостью Б.
Сечение на виде спереди имеет вырожденный вид и совпадает с изображением плоскости Б. Точки 1,2,3, являются точками пересечения ребер пирамиды с плоскостью Б.
Для построения сечения на виде сверху достаточно найти указанные точки на этом виде и соединить их (с учетом видимости) отрезками прямых.
Эту же задачу (построения сечения) можно свести к задаче построения линии пересечения двух плоскостей, т.к. каждый отрезок ломаной линии сечения есть линия пересечения плоскости Б с той или иной гранью пирамиды.
Натуру сечения построим с помощью дополнительного вида по направлению фронтали f- перпендикулярной наклонной плоскости Б. Отметим базы отсчета глубин (т.к. сохраняются глубины точек).. На виде сверху удобно базу отсчета провести через дальнюю точку сечения, т.3. На дополнительном виде база отсчета проводится на свободном поле чертежа перпендикулярно линиям связи (направлению проецирования). Замеряя глубины точек 1,2,3 на виде сверху, откладываем полученные величины на соответствующих линиях связи от базы отсчета на дополнительном виде. Полученные точки соединяем между собой ломаной линией.
Натуру сечения можно определить иначе - способом засечек. Для этого нужно найти натуральную величину сторон 1-2,2-3,3-1 способом прямоугольного треугольника.
Дата добавления: 2017-11-21; просмотров: 1289;











