Фундаментальной науки

Являясь дальнейшим развитием традиционной начертательной геометрии, ко- торая имеет в настоящее время статус прикладной науки, системная начертатель-ная геометрия, имеющая свою аксиоматику, обладает всеми признаками самосто-ятельной геометрической системы и поэтому естественно является фундамента-

льной математической дисциплиной, имеющей большое прикладное значение.

С одной стороны, она раскрывает конструктив-ные cвойства идеальных форм проектируемых объектов, локализованных в эвклидовом прост-ранстве, а с другой, применяя различные проек-ционные аппараты, разрабатывает графические технологии построения и взаимного преобразо-вания обратимых изображений этих объектов, локализованных в картинном пространствве.

Отсюда следует, что аксиоматическому опи-санию изобразительных свойств тех или иных проекций этих объектов обязательно пред шест-вует структурный эвклидов анализ их идеальной геометрической формы как её своеобразная «об-работка» для последующего графического моде-лирования. Другими словами, аппарат эвклидо-вой геометрии в структуре системной начертате-льной геометрии является обязательным струк-туррным элементом.

Образно взаимосвязь евклидовой и начерта-тельной геметрий можно представить в виде ги-потетического дерева [ 93]. ( рис.2.1).

Разветвлённые «корни» этого дерева погру-жены в эвклидово пространство, элементами ко-торого являются понятия точек, линий, плоскос-тей и поверхностей. Эти элементы, как свое образные «питательные вещества», поступают в эту «корневую систему» и там, подчиняясь конст-руктивно-композиционным мыслям, образуют со-ответствующие системы, вступая только в те от-ношения и связи, которые описываются группа-ми аксиом сочетания, порядка, непрерывности и движения эвклидовой геометрии.

Рис.2.2.Архитектурный системный стандарт: здание строительной фирмы «Никаган Тауэр» во Флоренции.1970-е г. Арх. Курокава

Рис.2.3. Церковь Иоанна Предтечи Ширкова погоста.

Ритмы в построении вертикальной объёмной коипозиции

При этом первые 4 группы аксиом описывают взаимную принадлежность, пересечение, касание и параллельность, которые определяют позиционные свойства геометрической, т.е., идеальной формы объекта, а группа движения порождает и описывает конгруэнтность, равенство, тождественность и пер-пендикулярность элементов объектов-систем, которые определяют её метричес-кие свойства.

Разумеется, что такое распределение элементов и связей между ними требует

четкого представления условийтого или иного их взаимного расположения, кото-рые описываются позиционными теоремами эвклидовой геометрии.

Процедура такого избирательного образования геометрических систем по сути дела является процессом проектного мышления, воспитание и развитие которого является главной целью профессионального становления специалиста.

Как результат такого образа мышления в концептуальном пространстве созна-ния возникает вполне определённый воображаемый объект, информация про по-зиционные и метрические свойства идеальной формы которого требует, как прави-ло, графического кодирования в виде обратимых изображений. В этом случае те-чение творческой мысли заставляет человека брать в руку карандаш и двигать его концом-точкой по плоскому листу бумаги, устанавливая взаимно-однозначные со-ответствия между точками и линиями воображаемого объекта и соответствующи-ми элементами графических конструкций на бумаге. А это, в свою очередь, вызы-вает в нашем дереве соответствующее движение образованных в его «корневой системе» геометрических объектов-систем по стволу до тех или иных «скелетных веток», в начале которых расположены проекционные аппараты получения обра-тимых изображений. Подвергшись проецированию этими аппаратами, наши воображаемые объекты преобразовываются в соответствующие их структурам комплексные ортогональные, аксонометрические, перспективные и другие черте-жи. Количество таких «скелетных веток» равно количеству видов проекций и каждая их них имеет «ветки первого порядка» связей и отношений, на которых, в свою очередь, есть «плодовые веточки» второго порядка с «плодами» этого дерева в виде «листочков» с искомыми обратимыми изображениями.

Нетрудно видеть, что исходной причиной кризисного состояния традиционной начертательной геометрии является совершенно абстрактное представление о геометрической природе изображаемого объекта как о пространственной форме или о множестве точек. Первое является абсурдным, так как каждый объект имеет свою конкретную форму, но не является ею. Второе неконструктивно, и потому не подлежит графическому моделированию.

Между тем, логика возникновения и развития начертательной геометрии как науки об обратимых изображениях объектов, необходимых человеку, требует прежде всего, ясного представления исполнителя изображения о природе того, что изображается. Поэтому системное понимание природы любого проектируемого объекта совершенно естественно. Ведь в родственных изобразительных дисци-плинах – рисунке и живописи, изучение пластической анатомии человека, т.е., мор-фологии человеческого тела, без знания которого немыслимо его грамотное худо-жественное изображение, считается обязательным.

Но свою «анатомию» имеет любой как существующий, так и проектируемый объект. Эта анатомия называется его структуройкак совокупностью устойчивых взаимосвязей между элементами, интегрирующей их в единое целое. Познание ст-руктуры существующего объекта сводится к выяснению или анализу того, из каких элементов он состоит и какими связями и отношениями они взаимосвязаны. Такой характер познания присущ всем представителям естественных наук, изучающим реально существующие и непознанные объекты и явления материального мира. Если же объект не существует, то его структуру познать невозможно, а в случае необходимости его существования требуется прежде мысленно синтезировать эту структуру на основе представления об её элементах и характере связей между ними. В итоге в сознании формируется образ или геометрическая модель несу-

ществующего объекта, которая служит «натурой» для её графического моделиро-

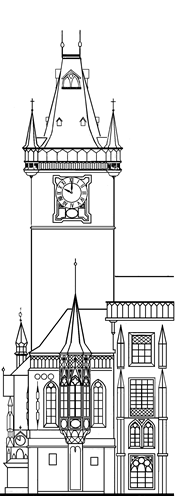
Рис.2.4. Городская ратуша на

Староместской площади в Праге

Рис.2.5. Мавзолей Саманидов в Бухаре

Объёмная композиция, построенная на

метрическом повторе

вания, лежащего в основе создания проектной модели объекта как документа на

материализацию его структуры в реальном пространстве.

С понятием о структуре объекта тесно связано понятие о его форме как о «внутренней организации содержания» [83,122], где содержание понимается как «определённым образом упорядоченная совокупность элементов и процессов, образующих предмет или явление». Нетрудно видеть, что понятие о содержании

адекватно понятию о системе, а под формой объекта можно пониматьматериа-лизованную структуру его пространства.

В связи с тем, что понятия формы и формообразования в архитектуре, дизай-не, технике, искусстве являются фундаментальными, то геометрия, лежащая в ос-нове этих видов творческой деятельности человека, должна раскрывать сущность этих понятий присущими ей средствами.

В монжевых определениях целей начертательной геометрии дважды встреча-ется слово «форма», однако это понятие этой наукой не раскрывается, равно как оно не раскрывается и в эвклидовой геометрией. С этим трудно согласиться и поэтому в предлагаемой концепции системной начертательной геометрии морфо-логия объекта раскрывается по мере повествования, в итоге показывающего, что объект, локализованный в реальном пространстве, имеет одну действительную или истинную форму, он же, локализованный в визуальном пространстве зри-тельного восприятия, имеет множество видимых форм, соответствующих мно-жеству положений зрителя, он же, локализованный в концептуальном (эвклидо-вом) пространстве знаний, имеет единственную идеальную форму, а будучи рас-положенным в картинном пространстве, приобретает несколько условных форм тех видов проекций, в которых этот объект изображен. При этом разумеется, что в каждом пространстве форма объекта является результатом «материализации» его структуры, в результате которой возникает объект конкретного устройства, стро-ения или конструкции. Поэтому позиционными и метрическими свойствами обла-дает не сам объект, а его конкретная форма. Понимание этих идей является на-чалом формирования профессионального конструктивно-композиционного мышле-ния студентов архитекторов, дизайнеров, конструкторов. В основу дальнейшего развития этой формы мышления должно лечь осознанное понимание структуры объекта, т.е., чёткое представление о видах связей и отношений между его элементами, их конструктивных возможностях и свойствах.

Это обстоятельство требует системной интерпретации аксиоматики геометрии эвклидова пространства, которая описывает эти связи и отношения и является предметом дальнейшего преобразования в практические аксиоматики геометрий картинных пространств различных видов проекционных изображений. Поэтому в состав системной начертательной геометрии входит краткая системная интер-претация аксиом геометрии эвклидова пространства как аксиом его геометри-ческих систем [103].

Переход от системного представления о природе изображаемого объекта к си-стемному пониманию его проекционных изображений происходит на основе со-блюдения принципов проецирования, системности, модельности, изоморфизма, взаимности отношений между элементами геометрических и графических систем, алгоритмичности, экзактности (точности графических построений), движения и рациональности разрабатываемых геометро-графических технологий.

В зависимости от характеров этих принципов, курс системной начертательной геометрии включает в себя три информационных направления: морфологическое,о котором говорилось выше, технологическое, основанное на использовании принципа проецирования, лежащего в основе концептуального конструирования разных видов проекционных аппаратов метода двух изображений, гарантирующих

обратимость получаемых проекций, и геометро-графическое, в котором аксио-матически описываются изобразительные свойства этих проекций в виде опре-делений и утверждений, логически вытекающих из предварительного системного анализа конструктивного содержания позиционных и метрических свойств идеаль-

ной формы изображаемого объекта. Здесь под изобразительными понимаются та-

Рис.2.6. Преображенская церковь в Кижах, 1714 г.

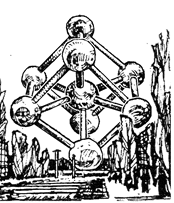
Рис.2.7. Новая монументальность. Атомизм в Брюсселе

кие свойства различных видов обратимых проекций, которые определяют харак-

терные, отличительные особенности их графической структуры.

Так как изобразительные свойства разных видов проекций однозначно кодиру-ют информацию о позиционных и метрических свойствах идеальной формы объек-та, то они становятся одними из предметов исследования системной начертатель-ной геометрии, а совокупность или система утверждений, определений и правил,

которые их аксиоматически описывают, становится её аксиоматикой..

Но в силу того, что каждый аппарат проецирования имеет свои конструктив-ные особенности, влияющие на характер изобразительных свойств получаемых ими проекций, получается, что одна и та же информация кодируется в разных про-екциях разными изобразительными свойствами, которые описываются соответ-ственно разными аксиоматическими утверждениями и определениями.

Отсюда следует, что системная начертательная геометрия в качестве своих подсистем имеет геометрии картинных пространств ортогональных, параллельных аксонометрических и центральных проекций, а также проекций с числовыми отмет-ками и др. Каждая из этих геометрий имеет свою аксиоматику, описывающую мор-фологическое, технологическое и геометро-графическое направление их содержа-

ния.

Фундаментальность этим геометриям придаёт содержание их технологических

направлений, прежде рассматривающих структуры геометрических аппаратов по-лучения и взаимного преобразования обратимых изображений, а затем - их гра-фических моделей. Минимизация структуры последних приводит к фундаменталь-ному понятию определителя изображения, впервые предложенному профессором Русскевичем Н.Л. [72] как неизменяемой графической конструкции, присоединён-ной к картинной плоскости и создающей в ней все условия для непосредственного и независимого построения и преобразования обратимых изображений, т.е., при-дающей картине свойства самостоятельного пространства. Если в этом простран-стве происходят такие преобразования его элементов, при которых каждое после-дующее является результатом произведения двух предыдущих, то в своей совоку-пности они образуют соответствующую группу преобразований.

В согласии с клейновой классификацией геометрических систем, основным предметом исследования геометрии того или иного пространства являются инва-рианты соответствующих групп преобразований их элементов. В нашем случае картинное пространство заполнено обратимыми изображениями и поэтому роль инвариантов групп их взаимных преобразований играют соответственные графи-ческие конструкции в виде определителей этих изображений. Как показали исследования [90], эти конструкции проективно эквивалентны бинарным моделям пространства R³ [27] професора Джапаридзе И.С., получаемым в результате «рационального» отображения, переводящего проективные соответствия в анало-гичные плоские, благодаря чему «операции на чертеже доводятся до минимума».

На этой основе в курсе системной начертательной геометрии все геометро-

графические технологии построения и преобразования обратимых изображений в различных видах проекций содержат минимально-возможное количество простых графических операций, и не содержат рутинных операций замера, откладывания и увеличения, резко снижающих точность построений [105].

Геометрии всех видов картинных пространств имеют широкие практические приложения в различных областях науки, техники и искусства.

Отличительной особенностью системного исследования конструктивных струк-тур элементов эвклидова пространства и их систем является рассмотрение всех вариантов как их ориентации в пространстве относительно выбранной системе отсчета, так и взаимного расположения относительно друг друга. Это даёт возмож-ность оценить рассматриваемую ситуацию в целом, а на основе анализа её каче-ственных и количественных характеристик делать соответствующие аксиомати-ческие утверждения и определения относительно выявленных изобразительных, позиционных и метрических свойств получаемых графических конструкций.

Рис. 2.8. Учебные упражнения по композиции из плоских геометрических фигур