ПРИЛОЖЕНИЕ 5. График Кокса
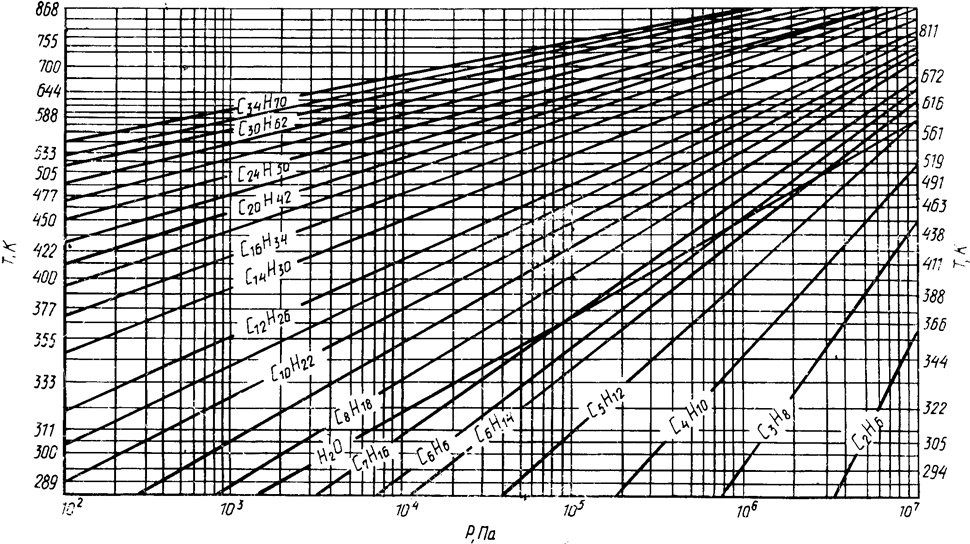
Пользование номограммой. На графике находим точку с координатами заданным давлением или температурой. Из найденной точки проводим равноудаленную от двух соседних лучей прямую до пересечения с вертикалью или горизонталью заданного углеводорода, соответствующей давлению этому давлению или температуре. Из полученной точки проводим горизонталь или вертикаль, параллельную оси абсцисс или ординат, до пересечения с осью на которой получим точку, соответствующую температуре или давлению.
ПРИЛОЖЕНИЕ 6. Номограмма для определения температуры кипения нефтепродуктов в зависимости от давления

Пользование номограммой. Через точку соответствующую заданному значению давления (правая шкала), провести прямую до пересечения с кривой (средняя шкала) температуры кипения заданного соединения при атмосферном давлении. Продолжение прямой укажет на температуру кипения соединения при заданном давлении (левая шкала)
Критические и приведенные параметры. При определенных значениях температуры и давления двухфазная система (жидкость – пар) может переходить в однофазную (пар), которая характеризует критическое состояние вещества. Температуру и давление, соответствующие этому состоянию, называют критическими. Для многих индивидуальных углеводородов они известны и приведены в различных литературных источниках [4, 5].
Приближенно критические параметры нефтяных фракций определяют с помощью графика (рис.1.2) по известным молярным массам, средним температурам кипения и относительной плотности.
Пример 1.8 Средняя температура кипения узкой бензиновой фракции при атмосферном давлении (»1×105 Па) составляет 127°С. Найти ее температуру кипения при давлении 2×105 Па.
Решение. На графике Кокса (прил. 5) находим точку с координатами 105 Па и 127°С (400 К). Из найденной точки проводим равноудаленную от двух соседних лучей прямую до пересечения с вертикалью, соответствующей давлению 2×105 Па. Из полученной точки проводим горизонталь, параллельную оси абсцисс, до пересечения с осью ординат, на которой получим точку, соответствующую температуре 151°С (424 К). Эта температура и является температурой кипения фракции при давлении 2×105 Па.
Пример 1.9 При вакуумной разгонке нефтяного остатка в стандартном аппарате АРН-2 при давлении 133,3 Па была получена фракция 196-213°С. Каковы пределы выкипания этой фракции при атмосферном давлении?
Решение. Воспользуемся номограммой прил. 6. На правой шкале отметим остаточное давление 133,3 Па (1 мм рт.ст.), на левой – температуры начала и конца кипения фракции при данном давлении. Тогда на средней шкале получим точки, соответствующие температурам кипения при атмосферном давлении: 400°С и 420°С.
Таким образом, искомая фракция выкипает в пределах 400-420°С при атмосферном давлении.
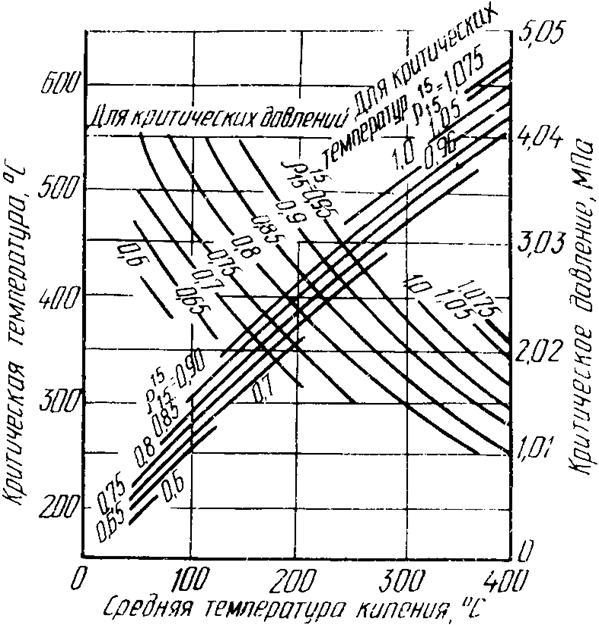
Рисунок 1.2 – График для определения критических температур и
давлений нефтепродуктов разной плотности
Более точно критическую температуру Ткр (в кельвинах) и давление rкр (в паскалях) можно найти по уравнениям:
Ткр=355+0,97а+0,00049а2; (1.6)
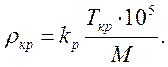 (1.7)
(1.7)
Константы а и kp, входящие в уравнения (1.6) и 1.7), рассчитываются по формулам:
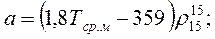
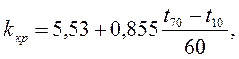
где t10, t70 – температуры отгона 10 и 70% нефтепродукта по ГОСТ 2177-82, °С.
Константа kp имеет численные значения для парафиновых углеводородов 5,0-5,3; нафтеновых 6,0; ароматических 6,5-7,0; нефтепродуктов прямой перегонки 6,3-6,4 [2].
При определении константы а вместо средней молярной температуры кипения нефтяной фракции приближенно можно взять температуру ее 5-%-го отгона. Последняя также входит в упрощенную формулу подсчета критической температуры [1]:
Ткр=1,05Тср+146.
При расчете тепловых и некоторых других свойств нефтепродуктов применяют так называемые приведенные температуру и давление.
Приведенная температура (Тпр) представляет отношение температуры нефтепродукта (Т, К) в заданных условиях его критической температуре (Ткр, К):
Тпр=Т/Ткр. (1.8)
Приведенное давление (rпр) – это отношение давления в системе (r, Па), в которой находится нефтепродукт, к его критическому давлению (rкр, Па):
rпр=r/rкр. (1.9)
Фугитивность. Нефтепродукты и их пары не всегда являются идеальными системами. При невысоких давлениях и повышенных температурах они подчиняются законам Рауля и Дальтона
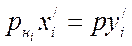 или
или 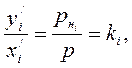 (1.10)
(1.10)
где 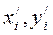 – молярная доля i-го компонента в жидкой и паровой фазе;
– молярная доля i-го компонента в жидкой и паровой фазе; 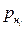 – давление насыщенных паров i-го компонента, Па; р – общее давление в системе, Па;
– давление насыщенных паров i-го компонента, Па; р – общее давление в системе, Па; 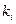 – константа фазового равновесия.
– константа фазового равновесия.
Большие давления и низкие температуры вызывают более или менее значительное отклонение от идеального состояния, и в расчетные формулы необходимо вводить поправки. В этих случаях выражение для константы фазового равновесия (1.10) можно записать в виде
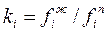 или
или 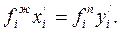
Здесь величины 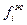 и
и 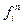 представляют собой фугитивность жидкости и ее паров. Фугитивность измеряется в тех же единицах, что и давление, и заменяет его в уравнениях идеального состояния. Это позволяет использовать последние для реальных газов и жидкостей.
представляют собой фугитивность жидкости и ее паров. Фугитивность измеряется в тех же единицах, что и давление, и заменяет его в уравнениях идеального состояния. Это позволяет использовать последние для реальных газов и жидкостей.
В общем случае фугитивность является функцией приведенных температуры и давления. Для практических целей фугитивность находят по графикам [1, 2, 6, 7], один из которых приведен на рис.1.3.
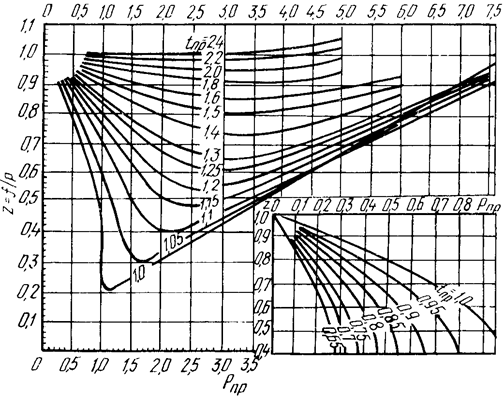
Рисунок 1.3 – График для определения коэффициента фугитивности
(сжимаемости) нефтепродуктов
Пользование номограммой. Через точку соответствующую заданному значению приведенного давления, провести прямую до пересечения с кривой заданного значения приведенной температуры. Из полученной точки пересечения провести горизонтальную прямую до шкалы коэффициентов сжимаемости. Точка пересечения дает искомое значение.
Ось ординат этого графика представляет собой отношение фугитивности к реальному давлению:
z=f/p. (1.11)
Безразмерная величина z носит название коэффициента фугитивности. Иногда его называют коэффициентом сжимаемости [7]. Хотя коэффициент сжимаемости имеет несколько иной физический смысл, при проведении приближенных расчетов можно допустить равенство названных коэффициентов.
Пример 1.12 Найти фугитивность фракции 62-85°С при 220°С и 2,5 МПа. Критические параметры tкр=247°С и ркр=3,56МПа.
Решение. Определим приведенные температуру и давление:
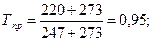
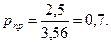
По графику (см. рис.1.3) находим коэффициент сжимаемости z=0,57. По формуле (1.11) фугитивность равна f=zp=1,43 МПа.
Пример 1.13 Определить константу фазового равновесия k для н-пентана при 115°С и 1,2 МПа. Его критические параметры: tкр=0,57×2,5=3,34 МПа.
Решение. Найдем фугитивность для паровой фазы н-пентана. Приведенные параметры
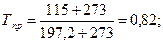
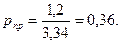
По графику (см. рис.1.3) определим z=0,76 и fп=0,76×1,2=0,91 МПа.
Жидкая фаза находится при той же температуре, но под давлением собственных насыщенных паров рн, которое определим по графику Кокса (прил.5): рн=0,8 МПа. Приведенное давление в этом случае
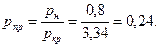
Коэффициент сжимаемости для жидкой фазы (см. рис.1.3) z=0,81, фугитивность жидкой фазы fж=0,81×0,8=0,65 МПа. Константа фазового равновесия определится как отношение фугитивностей
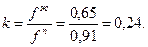
Кроме рассмотренного способа, константу фазового равновесия можно находить по номограммам (прил.7, 8).
ПРИЛОЖЕНИЕ 7. Таблица перевода значений кинематической вязкости (мм2/с) в условную (°ВУ)
| мм2/с | °ВУ | мм2/с | °ВУ | мм2/с | °ВУ | мм2/с | °ВУ | мм2/с | °ВУ |
| 1,00 | 2,48 | 4,33 | 6,28 | 8,26 | |||||
| 1,10 | 2,60 | 4,46 | 6,42 | 8,40 | |||||
| 1,20 | 2,72 | 4,59 | 6,55 | 8,53 | |||||
| 1,29 | 2,83 | 4,72 | 6,68 | 8,66 | |||||
| 1,39 | 2,95 | 4,85 | 6,81 | 8,80 | |||||
| 1,48 | 3,07 | 4,98 | 6,94 | 8,93 | |||||
| 1,57 | 3,19 | 5,11 | 7,07 | 9,06 | |||||
| 1,67 | 3,31 | 5,24 | 7,20 | 9,20 | |||||
| 1,76 | 3,43 | 5,37 | 7,33 | 9,34 | |||||
| 1,86 | 3,56 | 5,50 | 7,47 | 9,48 | |||||
| 1,96 | 3,68 | 5,63 | 7,60 | 9,61 | |||||
| 2,05 | 3,81 | 5,76 | 7,73 | 9,75 | |||||
| 2,15 | 3,95 | 5,89 | 7,86 | 9,88 | |||||
| 2,26 | 4,07 | 6,02 | 8,00 | 10,01 | |||||
| 2,37 | 4,20 | 6,16 | 8,13 | 10,15 |
Дата добавления: 2017-11-21; просмотров: 9746;











