Уравнение неразрывности идеальной жидкости в дифференциальной форме
Гидродинамика. Основные понятия и определения
Гидродинамика – раздел гидравлики, изучающий движение жидкости в зависимости от сил к ней приложенных, ее взаимодействие с твердыми телами и стенками, ограничивающими ее движение.
Жидкость рассматривается как континуум, состоящий из частиц. В процессе движения изменяются взаимное расположение частиц жидкости и их форма. Последнее зависит от свойств, которыми наделяется жидкость. Если жидкость предполагается идеальной, то форма частиц изменяется только за счет формы канала в котором происходит движение. Если жидкость способна сжиматься и обладает вязкостью, то форма частиц изменяется не только за счет взаимодействия со стенками канала, но и в результате взаимодействия частиц друг с другом, которое характеризуется нормальными и касательными напряжениями на гранях выделенного элементарного объема.
Существует два способа описания движения жидкости: способ Лагранжа и способ Эйлера.
Способ Лагранжа предполагает рассмотрение движения каждой частицы жидкости. При этом
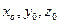- начальные координаты частицы;
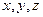- координаты частицы жидкости в произвольный момент времени 
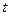, тогда:
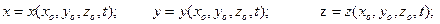
| (5.1) |
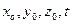- называют переменными Лагранжа.
Способ Эйлера предусматривает описание движения жидкости функциями, выражающими изменение скоростей в точках неподвижной области, выбранной в пределах потока (массы движущейся жидкости). По Эйлеру в точке рассматриваемой области, определяемой координатами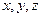 
, находится частица жидкости, имеющая скорость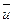 
 ,
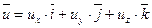| (5.2) |
где
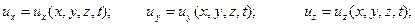
| (5.3) |
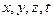- называют переменными Эйлера.
Совокупность формул (5.1) описывает траекторию движения частицы жидкости с начальными координатами 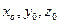. Используя эти уравнения можно найти проекции на координатные оси вектора скорости и вектора ускорения рассматриваемой точки.
Формулы (5.3) определяют в выбранной области (точка с координатами 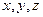) составляющие местной скорости в момент времени 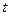. Эту скорость называют мгновенной местной скоростью. Совокупность мгновенных местных скоростей в рассматриваемой неподвижной области образует векторное поле – поле скоростей. В общем случае в каждый новый момент времени оно может измениться.
Линия, в каждой точке которой в данный момент времени вектор мгновенной местной скорости 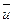направлен по касательной, называется линией тока (рис. 5.1).
Как следует из определения, составляющие скорости 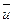, нормальные к линии тока, в любой точке этой линии равны нулю.
Если в рассматриваемый момент времени выделить в области, через которую движется жидкость, замкнутый, не пересекающий себя контур, то через каждую точку этого контура будет проходить только одна линия тока. Совокупность линий тока, проведенных через все точки этого контура, образует поверхность, которую называют трубкой тока. Жидкость, движущуюся внутри трубки тока, образует струйку. Внутри трубки жидкость движется не пересекая ее поверхности, т.к. скорости частиц направлены по касательным к линиям тока, образующим трубку. Если контур ограничивает бесконечно малую площадку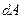 
, то струйку называют элементарной; если контур ограничивает конечную площадку 
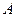, струйку называют конечной.
|
Рис. 5.1
Поверхность нормальная в каждой своей точке линиям тока называется живым сечением. Для элементарной струйки мгновенные местные скорости в пределах живого сечения можно считать одинаковыми и говорить о местной скорости элементарной струйки. Для конечной струйки значения местных скоростей в пределах живого сечения, как правило, не остаются постоянными. По длине струйки площадь живого сечения и мгновенные скорости могут изменяться.
Движение жидкости по характеру изменения во времени поля скоростей можно классифицировать на неустановившееся (нестационарное), когда местные скорости изменяются во времени (справедливы формулы (5.3)) и установившееся (стационарное), когда поле скоростей не изменяется
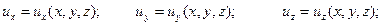
| (5.4) |
При установившемся движении траектории и линии тока совпадают, а в общем случае неустановившегося движения траектории и линии тока не совпадают. В частном случае неустановившегося движения, когда во времени изменяются только модули скоростей, а направления векторов не изменяются, линии тока и траектории также совпадают.
Необходимо подчеркнуть, что при установившемся движении струйки жидкости существуют физически, т.к. непроницаемые трубки тока неизменны во времени. При неустановившемся движении, в связи изменением поля скоростей, струйки являются только мгновенными, в силу того, что трубки тока непрерывно изменяются.
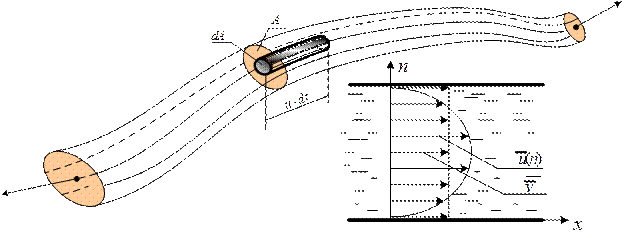
Расходом струйки называют объем жидкости, проходящей через живое сечение в единицу времени (рис. 5.2). Для элементарной струйки с равномерным распределением скорости по площади 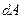имеем
 .
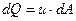| (5.5) |
Для конечной струйки при определении расхода необходимо учитывать изменение скорости движения частиц по площади живого сечения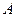
 .
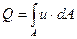| (5.6) |
Для упрощения расчетов целесообразно ввести понятие средней скорости в рассматриваемом живом сечении конечной струйки
 ,
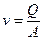| (5.7) |
и тогда расход можно определить как произведение средней скорости на площадь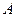
 .
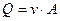| (5.8) |
|
Рис. 5.2
Поток жидкости. Понятия и характеристики
Потоком жидкости в гидравлике называют движущуюся массу жидкости, ограниченную твердыми поверхностями, поверхностями раздела жидкостей и свободными поверхностями. В зависимости от того какие поверхности ограничивают поток различают потоки безнапорные, напорные и гидравлические струи (рис. 5.3).
Безнапорный поток ограничен частично твердой, частично свободной поверхностью (масса воды в реке, в канале, трубе отвода стоков, рис.5.3а).
Напорный поток ограничен каналом, образованным твердыми поверхностями, все сечение которого заполнено жидкостью (вода в трубах системы водоснабжения, рис.5.3б).
Гидравлическая струя – это поток жидкости ограниченный только газовой средой или другой жидкостью (поток жидкости, выбрасываемый из пожарного брандспойта, рис.5.3в).
а) б) в)
|
Рис.5.3
На поток легко распространить введенные понятия: линия тока, трубка тока, элементарная струйка, живое сечение, объемный расход.
Площадь живого сечения потока рассматривается, как сумма площадей живых сечений элементарных струек
 .
| (5.9) |
Живое сечение потока может быть ограничено линией, часть точек которой соприкасается с твердыми стенками канала, направляющего движение жидкости. Длина этой части контура живого сечения называется смоченным периметром. На рис. 5.3а) и б) смоченный периметр показан тонкой прерывистой линией. На первом рисунке он равен (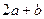 
), а на втором – ( 
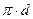). Обозначается смоченный периметр буквой греческого алфавита 
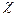(хи).
Отношение площади живого сечения к смоченному периметру называют гидравлическим радиусом
 .
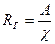| (5.9) |
Гидравлический радиус, это будет показано ниже – важная характеристика, используемая при определении расхода через живое сечение. В напорном потоке для круглого сечения диаметро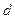м 
имеем
 .
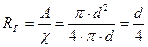| (5.10) |
Важной характеристикой потока является расход жидкости. Расход жидкости может определяться в единицах объема, единицах массы и единицах веса. Соответственно различают объемный, массовый и весовой расходы жидкости.
Расход жидкости – это количество жидкости протекающей через живое сечение в единицу времени. Согласно определению (см. (5.10)), расход измеряется в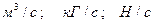 
.
 ,
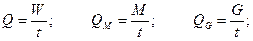| (5.11) |
где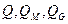 
- объемный, массовый и весовой расходы, соответственно;
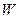- объем жидкости, протекающей через живое сечение потока за время ;
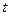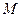- масса жидкости, протекающей через живое сечение потока за время ;
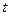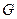- вес жидкости, протекающей через живое сечение потока за время .
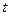Очевидно и то, что расход потока можно определить как сумму расходов элементарных струек, которые можно выделить в потоке
 .
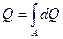| (5.12) |
Аналогично (5.7) и (5.8) определяется важная характеристика потока средняя скорость потока в рассматриваемом сечении
| .
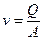| (5.13) |
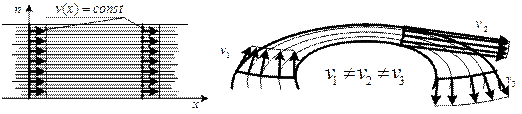
Введение понятия о средней скорости потока позволяет проще решать практические задачи. Важным с точки зрения практики является установившийся режим движения потока, который, в свою очередь подразделяют на равномерное и неравномерное движения.
а) б)
|
Рис. 5.4
Равномерное движение (рис.5.4а) характеризуется параллельностью и прямолинейностью линий тока, постоянством формы и размера живого сечения, средней скоростью по длине потока. Неравномерное движение (рис. 5.4б) отличается не параллельностью линий тока, изменением площади и формы живого сечения, изменением средней скорости по длине потока.
С практической точки зрения среди неравномерных движений выделяют плавно изменяющееся движение (рис.5.5), отличающееся следующими признаками: линии тока имеют малую кривизну, живые сечения можно считать плоскими, а их форма и площадь от сечения к сечению меняются плавно.
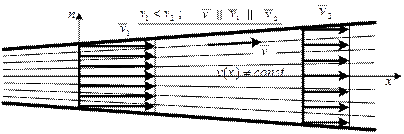Рис. 5.5
|
Средняя скорость в сечении – это условная скорость для всех точек потока в живом сечении, при которой обеспечивается реальный расход потока в заданном сечении. Используя понятие средней скорости потока, можно записать уравнение неразрывности потока несжимаемой жидкости
| |
 .
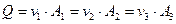| (5.14) |
Лекция 6
Уравнение Бернулли
Дифференциальные уравнения движения идеальной жидкости
В движущейся идеальной жидкости, плотность которой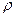 
, выделим элементарный параллелепипед размерами 
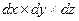и запишем дифференциальные уравнения движения этого объема жидкости в координатной форме, рассматривая его как материальную точку.
На элемент действуют составляющие сил давления и массовых сил, интенсивность которых на единицу массы по направлению осей равна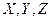 
(рис. 6.1).
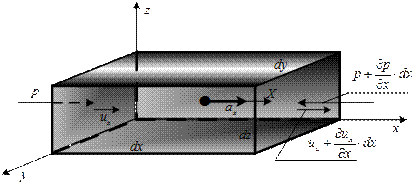Рис. 6.1
|
На рисунке показаны только составляющая массовых сил по оси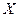 
, давление на гранях перпендикулярных оси 
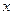и составляющая ускорения по оси 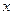, что позволяет записать уравнение движения выделенного объема в направлении оси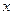
 .
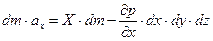| (6.1) |
Так как масса элементарного объема легко определяется через массовую плотность
 ,
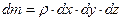| (6.2) |
то после деления обеих частей уравнения (6.1) на (6.2), получаем
 .
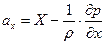| (6.3) |
С учетом того, что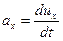 
, где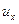 
– проекция скорости элементарного объема на ось 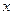, уравнение (6.3) принимает вид
 .
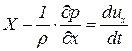| (6.4) |
Действуя аналогично можно получить уравнения движения выделенного элемента в направлении осе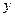й 
и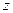 
. Таким образом система дифференциальных уравнений движения идеальной жидкости в декартовой прямоугольной системе координат имеет вид
,  , 
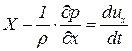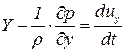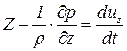
| (6.5) |
Уравнение Бернулли для установившегося движения при действии
потенциальных сил
Последовательно умножим уравнения (6.5) на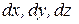 
и сложим полученные результаты
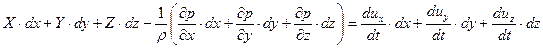
| (6.6) |
При установившемся движении
 ,
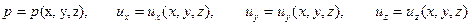| (6.7) |
тогда в рассматриваемый момент времени
 .
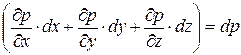| (6.8) |
В движущейся жидкости размеры элементарного параллелепипеда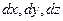 
можно определить через составляющие скорости частицы 
 .
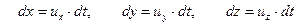| (6.9) |
С учетом (6.9) правая часть уравнения (6.6) приводится к виду
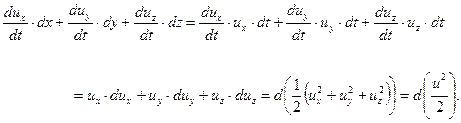
| (6.10) |
Если движение жидкости происходит в потенциальном силовом поле, то составляющие интенсивности массовых сил определяются через потенциальную энергию этого поля, приведенную к единице массы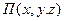 
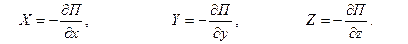
| (6.11) |
Принимая во внимание (6.11), первое слагаемое в левой части уравнения (6.6) можно записать так
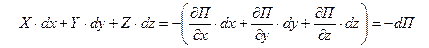
| (6.12) |
С учетом (6.8), (6.10), (6.12) уравнение (6.6) принимает следующий вид
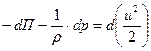
| (6.13) |
Так как идеальная жидкость – это несжимаемая жидкость, и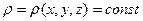 
(6.13) можно записать в виде
 ,
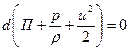| (6.14) |
или
 .
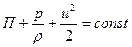| (6.15) |
Уравнение (6.15) и является уравнением Бернулли для элементарной струйки идеальной жидкости при установившемся движении, когда элементарную струйку можно отождествлять с линией тока. Для различных линий тока значения константы в уравнении (6.15) будут разными.
Замечание. Более детальное изучение движения частицы жидкости позволяет установить, что при изменении положения в пространстве происходит изменение ее формы и объема. Движение можно представить как сумму трех движений: поступательного (вместе с полюсом), деформационного (за счет изменения размеров) и вращательного (вокруг мгновенной оси, проходящей через полюс).
По характеру движения частиц различаютвихревое и потенциальное движения.
Вихревым движением называют такое движение, при котором движущиеся частицы жидкости вращаются вокруг осей, проходящих через их полюсы. Вихревое движение характеризуется вихревыми линиями – линиями, в каждой точке которых касательная совпадает с вектором угловой скорости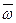 
.
Движение, при котором такое вращение отсутствует, называется безвихревым или потенциальным движением.
Уравнение Бернулли справедливо:
· вдоль линии тока;
· на вихревых линиях;
· при винтовом движении, когда векторы линейной и угловой скоростей параллельны (линия тока совпадает с вихревой линией);
· при потенциальном движении;
· при статическом равновесии жидкости.
Проведем детальное рассмотрение параметров, характеризующих движение жидкой частицы, но ограничимся только движением в плоскости xy (рис. 6.2).
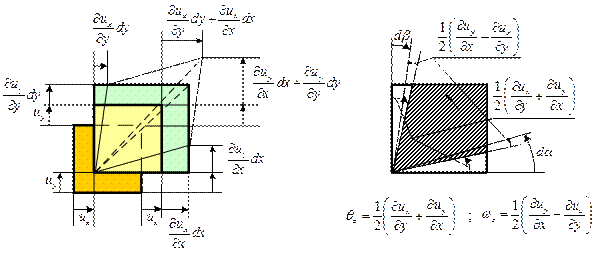Рис. 6.2
|
Частица жидкости в форме прямоугольного параллелепипеда (рис. 6.1) имеет в точке О локальную скорость, составляющие которой равны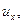 
, 
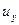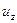. Если О полюс, движущейся частицы, за время 
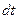сместится на расстояние 
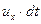в направлении оси x и на расстояние 
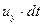в направлении оси y, то за счет приращения скорости в направлении осе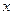й и 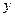ребра частицы получат абсолютные удлинения:
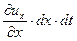 - по о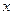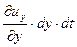си ;  - по оси .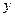
| (6.16) |
Кроме деформаций удлинения частица в окрестности точки О претерпевает деформации сдвига, характеризуемые углам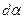и 
и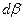 
 ;  .
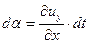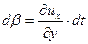| (6.17) |
Суммарную деформацию сдвига в плоскости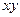 
равную 
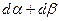можно разложить на две составляющие:
деформацию сдвига, характеризуемую углами
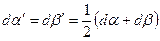
| (6.18) |
и поворот частицы относительно оси 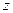, проходящей через полюс О, на угол
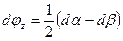
| (6.19) |
Следовательно, изменение положения и формы частицы в плоскости 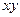характеризуется:
скоростями линейных относительных деформаций
 , 
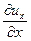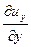
| (6.20) |
скоростью деформации сдвига
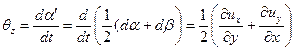
| (6.21) |
угловой скоростью вращения частицы относительно оси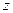
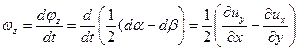
| (6.22) |
В общем случае деформационное движение частицы характеризуется:
скоростями линейных деформаций
, ,  ;
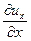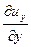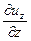| (6.23) |
скоростями угловых деформаций
 ;
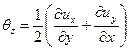
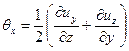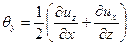
| (6.24) |
составляющими мгновенных угловых скоростей
 ;
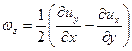
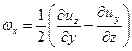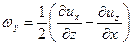
| (6.25) |
Вектор мгновенной угловой скорости 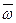направлен по нормали к плоскости в которой происходит вращение, а его модуль легко определяется по составляющим
 .
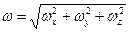| (6.26) |
С направлением вектора 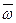связано определение вихревой линии – линии, в каждой точке которой вектор угловой скорости совпадает с направлением касательной к этой линии (рис.6.3).
Рис. 6.3
|
Дифференциальное уравнение вихревой линии имеет вид
 ,
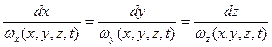| (6.27) |
где 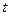рассматривается как параметр.
Уравнение неразрывности идеальной жидкости в дифференциальной форме
При изучении движения жидкости интенсивность массовых сил 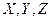обычно считается известной. Неизвестными являются функции 
, 
, 
, 
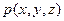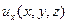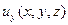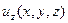– всего четыре неизвестных функции. Определяемые функции должны удовлетворять уравнениям Эйлера (6.5). Поскольку число неизвестных превышает число уравнений, к уравнениям Эйлера необходимо присоединить уравнение неразрывности в дифференциальной форме.
Уравнение неразрывности, записанное для элементарного объема жидкости в форме прямоугольного параллелепипеда размерами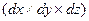 
(см. рис.6.1) можно получить на основании следующих рассуждений.
Гипотеза сплошности, применительно к идеальной жидкости, предполагает, что за время 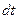объемы жидкости втекающей и вытекающей из элементарного параллелепипеда должны быть равны. Объемы жидкости втекающей через грани перпендикулярные осям 
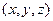легко найти по составляющим скорости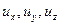 
 .
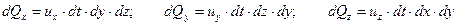| (6.28) |
Аналогичные объемы вытекающей жидкости, с учетом изменения скорости, равны
 .
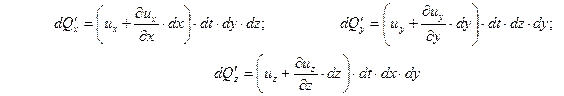| (6.29) |
Сплошность в рассматриваемом объеме не нарушится, если
  ,
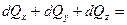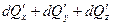| (6.30) |
что после подстановки (6.28) и (6.29) в (6.30) приводит к результату
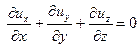
| (6.31) |
Уравнение (6.30) и есть уравнение неразрывности идеальной несжимаемой жидкости в дифференциальной форме.
Присоединив к уравнениям равновесия (6.5) уравнение неразрывности (6.31) получаем систему дифференциальных уравнений для определения четырех функций, характеризующих установившееся движение жидкости.
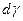
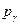
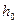
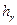
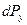
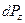
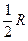
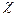
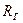
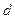
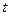
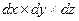
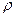
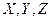
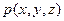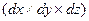
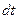
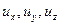
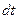
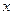
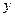
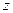
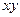– О
Уравнение Бернулли для струйки в поле силы тяжести
Если ось 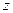направить по линии действия силы тяжести вверх, то из (6.12) получим
 ,  ,  , 
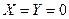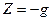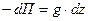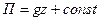
| (6.32) |
и уравнение (6.15) принимает вид
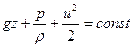
| (6,33) |
или
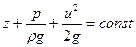
| (6.34) |
Если записать уравнение Бернулли для частицы жидкости при установившемся движении в двух ее положениях на линии тока (она совпадает с траекторией), то получим
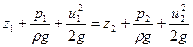
| (6.35) |
Уравнение Бернулли для струйки в криволинейном канале,
вращающемся с постоянной угловой скоростью
В том случая, когда жидкость движется в криволинейном канале, вращающемся с постоянной угловой скоростью, и линия действия силы тяжести параллельна оси вращения канала (рис.6.4), массовые силы, включая силу инерции в переносном движении, отнесенные к единице массы равны
 .
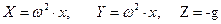| (6.36) |
Здесь учтены силы инерции в переносном движении, связанные с нормальным ускорением и сила тяжести. Сила инерции, определяемая кориолисовым ускорением, не рассматривается, т.к. она не влияет на движение частицы жидкости в направлении ее относительного движения.
Тогда, полагая
 ,
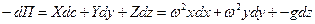| (6.37) |
после интегрирования найдем потенциал массовых сил
 ,
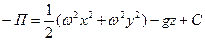| (6.38) |
или
 .
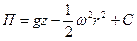| (6.39) |
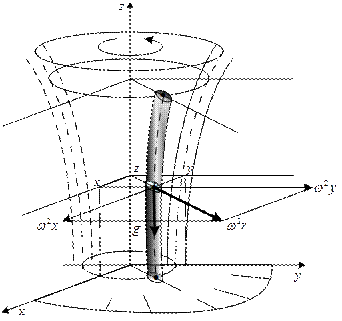Рис.6.4
|
Уравнение Бернулли (6.15) принимает вид
 ,
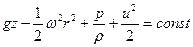| (6.40) |
или
 .
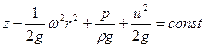| (6.41) |
Для двух сечений элементарной струйки можно записать
 .
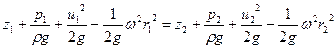| (6.42) |
Здесь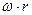 
есть угловая скорость в переносном движении.
Геометрическая интерпретация уравнения Бернулли для струйки идеальной жидкости
Каждое слагаемое в уравнении (6.34) можно рассматривать, как составляющую энергии частицы, отнесенную к единице веса.
Если за плоскость сравнения принять плоскость с нулевой потенциальной энергией, то:
- потенциальная энергия единицы веса определится формулой
 ;
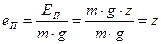| (6.42) |
- удельная кинетическая энергия составит
 ;
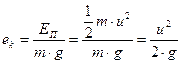| (6.42) |
- удельная энергия давления будет равна
 .
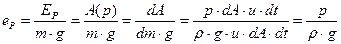| (6.42) |
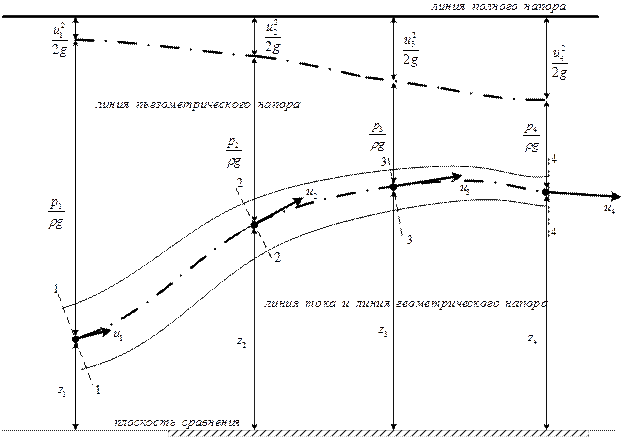
Для удельной энергии и ее составляющих, в гидравлике применяют следующие термины и обозначения:
H - гидродинамический или полный напор;
z - геометрический напор;
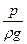- пьезометрический напор;
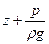- гидростатический напор;
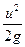- скоростной или кинетический напор.
|
Рис. 6.5. Геометрическая интерпретация уравнения Бернулли для струйки идеальной жидкости.
Единицей измерения напора является единица длины. Ясно, что при движении идеальной жидкости отдельные составляющие полного напора могут изменяться, но полный напор остается величиной постоянной (рис. 6.5).
Лекция 7
Уравнение Бернулли для струйки реальной жидкости
потока реальной жидкости. Режимы движения жидкости
Уравнение Бернулли для струйки вязкой жидкости
Течение реальной жидкости, в отличие от течения идеальной, характеризуется наличием потерь энергии на преодоление сил сопротивления движению – в первую очередь это потери на преодоление сил трения, обусловленных вязкостью жидкости и ее трением о стенки канала. Поэтому в правую часть формулы (6.35) необходимо добавить слагаемое, которое и будет учитывать потери энергии струйки
 ,
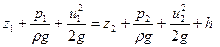| (7.1) |
где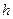 
-- потери напора на участке между сечениями 1-1 и 2-2.
Энергия, затраченная на преодоление сил вязкого трения, превращается из механической энергии в энергию тепловую. Процесс носит необратимый характер.
Уравнение Бернулли для потока вязкой жидкости
при установившемся движении
Если движение жидкости установившееся и плавно изменяющееся происходит в направлении оси x, то
 ;  ;  .
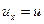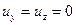| (7.2) |
В этом случае давление по живому сечению потока распределяется по гидростатическому закону, т.е.
 .
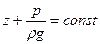| (7.3) |
Если поле скоростей имеет искривленные линии тока, гидростатический закон распределения давления в живом сечении нарушается, но при достаточной плавности потока этим фактом можно пренебречь (рис.7.1).
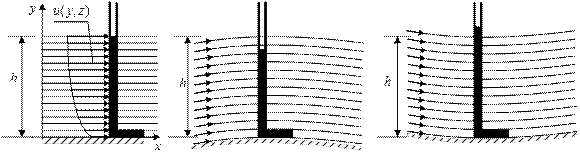Рис. 7.1
|
При переменной по сечению скорости частиц жидкости ( 
), удельную кинетическую энергию массы жидкости, протекающей через живое сечение потока A можно рассчитать по формуле
 ,
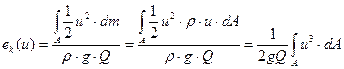| (7.4) |
где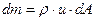 
- масса жидкости, которая прошла через сечение за единицу времени.
В общем случае вычисления по формуле (7.4) невозможны, т.к. функция 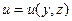неизвестна. Целесообразно воспользоваться средней скоростью потока в сечении v
 .
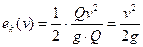| (7.5) |
Заменить в уравнении Бернулли для потока удельную кинетическую энергию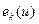 
на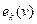 
можно, если ввести коэффициент кинетической энергии (коэффициент Кориолиса)
 .
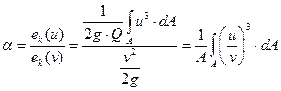| (7.6) |
В этом случае
 .
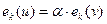| (7.7) |
Коэффициент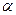 
определяется для всех практически значимых случаев течения потока экспериментально и характеризует отношение действительной кинетической энергии массы жидкости, протекающей через живое сечение потока, к кинетической энергии той же массы жидкости, вычисленной по средней скорости потока в сечении.
|
| Условия движения жидкости | ||
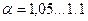
| - при прямолинейном турбулентном течении в трубах; | ||
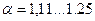
| - при прямолинейном турбулентном течении в открытых каналах; | ||
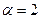
| - при прямолинейном ламинарном течении в трубах (теоретическое решение). |
Вводя в рассмотрение средние значения геометрического напора z и пьезометрического напора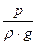 
, запишем для плавно изменяющегося потока, ограниченного жесткими стенками (канал, русло, трубопровод) уравнение Бернулли
 .
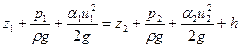| (7.8) |
Графическое толкование уравнения Бернулли для потока вязкой жидкости в предположении, что потери напора h линейно зависят от длины канала, приведено на рис. 7.2, где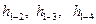 
- потери напора на участке между сечениями 1-2, 1-3, 1-4 соответственно. Линия полного напора в этом случае не остается горизонтальной, как при движении идеальной жидкости, а представляет линию нисходящую по направлению движения потока.
Для характеристики потерь напора на регулярном участке потока используют понятие гидравлического уклона. Гидравлический уклон – это величина средних потерь напора на единицу длины канала
 .
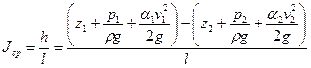| (7.9) |
Локальное гидравлического уклона характеризует скорость уменьшения полного напора потока по направлению его движения
 .
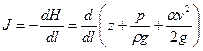| (7.10) |
Рис.7.2.
|
Классификация потерь напора
Потери напора при движении вязкой жидкости подразделяют на:
· потери напора на преодоление гидравлического сопротивления по длине, которые пропорциональны длине участков русла или трубы, направляющей движение потока;
· потери на преодоление гидравлических сопротивлений в пределах коротких участков, на которых имеются различные конструктивные нерегулярности – резкое сужение или расширение русла, внезапное увеличение или уменьшение диаметра трубы, поворот трубы или русла, устройства входа или выхода, трубопроводная арматура ( краны, задвижки, разветвления и т.д.).
| (7.11) |
Обычно потери напора определяют через скоростной напор и соответствующий коэффициент сопротивления 
 ,
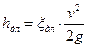| (7.12) |
 .
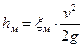| (7.13) |
Большинство зависимостей для определения коэффициентов сопротивления 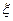или их конкретные значения установлены экспериментальным путем. На значения коэффициентов сопротивления влияет множество факторов:
· конструктивные формы и размеры;
· шероховатость стенок канала или трубы;
· скоростной режим течения жидкости;
· положение управляющих элементов запорной арматуры.
Одна из общих формул для определения потерь по длине – формула Дарси-Вейсбаха, для круглых труб имеет вид
