Принципы и основы векторного управления.
Принципы векторного управления.
Для получения высокого качества управления ЭП в статических и динамических режимах, при условии регулирования скорости υ в широких диапазонах (и в области малых скоростей υ), необходимо обеспечить возможность быстрого непосредственного управления моментом. Момент электродвигателя в каждый момент времени определяется величиной и фазой двух моментообразующих составляющих: основного магнитного потока и тока в силовой цепи двигателя (цепь якоря у ДПТ и цепь ротора у АД).
В ДПТ фазовая ориентация между моментом и током является неизменной и определена конструктивно, а именно фиксированным положением главных магнитов полюсов с обмотками возбуждения (магнитный поток) и щеточного узла (I якоря). Чтобы получить требуемое значение момента здесь достаточно управлять непосредственной и доступной для измерения величиной I якоря. ДПТНВ с быстродействующим регулятором тока якоря по управляемости идеально отвечает требованиям высокодинамичных ЭП (ЭП металлорежущих станков, ЭП прокатных станов).
В АД особенно в АД с короткозамкнутым ротором электромагнитные процессы протекают намного сложнее, токи и потокосцепления статора и ротора вращающегося с разными угловыми скоростями, имеет разные, изменяющиеся во времени фазовые параметры и не подлежат непосредственному измерению и управлению.
Доступной измеряемой и управляемой переменной в АД является ток статора. Для реализации векторного управления ток статора I представляют в виде двух ортогональных составляющих:
1 составляющая ток магнитного потока I1ψ
2 составляющая ток момента I1М

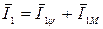
Фазовая ориентация этих двух составляющих определяется с помощью внешнего управляющего устройства, которое функционально можно сравнить с коллектором ДПТ. Другими словами в АД необходимо обеспечить управление, как амплитудой, так и фазой статора, т.е. управлять векторами тока статора (векторное управление).
Чтобы доказать возможность такого управления используем классическую теорию АД. Для этого рассмотрим обычную схему замещения АД:
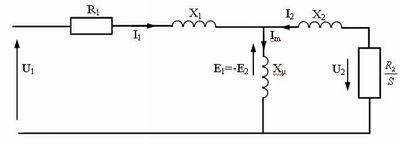 рис.32
рис.32
где R1,R2 – соответственно активное сопротивление обмоток фазы статора и ротора.
x1 – индуктивное сопротивление статора. x1 = ω0L1.
x2 – индуктивное сопротивление ротора. x2 = ω0L2.
xμ – индуктивное сопротивление рассеивания. xμ = ω0L12.
L1 – индуктивность статорной обмотки.
L2 – индуктивность роторной обмотки.
L12 – взаимная индуктивность между статорной и роторной обмоткой.
s – скольжение.
Электромагнитный момент М, развиваемый двигателем , выражают через параметры ротора:
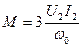 (1)
(1)
где U2 – индуктивное напряжение ротора.
I2 – ток ротора.
Поставим перед собой задаче выразить момент через ток статора I1, где 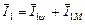
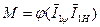
Для установления связи тока статора и параметров I2, U2 воспользуемся модифицированной схемой замещения АД, в которой за счет выбора коэффициентов приведения в качестве взаимной индуктивности используем, а =L12/L2 чтобы x2 = 0 тогда U2 = E2.
Тогда схема примет вид:
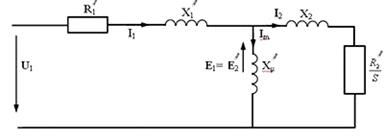 рис.33
рис.33
где R2’ – приведенное активное сопротивление обмотки ротора. 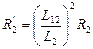
x1’ – приведенное индуктивное сопротивление статора. 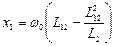
xμ' – приведенное взаимное индуктивное сопротивление 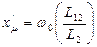
E2’ – приведенное ЭДС. 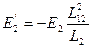
Ток статора в схеме делится на две составляющие:
1 составляющая моментообразующая I1М
2 составляющая потокообразующая I1ψ
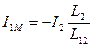 (2)
(2)
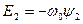 (3)
(3)
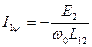 (4)
(4)
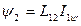 (5)
(5)
Получаем 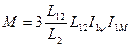 (6)
(6)
Уравнение 6 выражает зависимость электромагнитного момента АД через моментообразующую и потокообразующую составляющую тока статора и тем самым доказывает возможность управления моментом через воздействие на ток статора.
Векторная диаграмма АД, представим статор через две ортогональные составляющие:
Рис.34
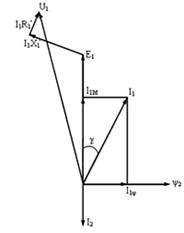
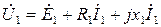
Из диаграммы: 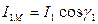
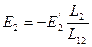
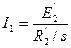
Тогда 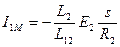 (7)
(7)
Объединяя уравнения (4) и (7) можно установить связь между I1М и I1ψ.
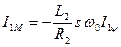
что позволяет определять угол γ через параметры ротора (R2) и нагрузку (s).
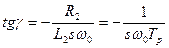 (8)
(8)
где Tp = L2/R2 – постоянная времени ротора.

Уравнение (8) позволяет сделать вывод, что каждому значению скольжения соответствует определенное соотношение составляющих тока статора.
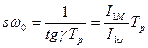 (9)
(9)
Уравнение (9) свидетельствует о том, что с помощью вектора тока статора и скольжения можно определить момент М в каждый момент времени.
Дата добавления: 2017-11-21; просмотров: 1246;











