ТЕОРЕТИЧЕСКИЕ ОСНОВЫ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

Позиционные задачи

Геометрически закономерное изображение пространственного объекта на плоскости достигается при помощи метода проецирования, который является основным методом в начертательной геометрии и инженерной графике [1].

Позиционными называют задачи, свя­занные с решением на комплексном чер­теже вопросов взаимного расположения геометрических объектов. Наибольший прак­тический интерес здесь представляют две группы задач: задачи на взаимную при­надлежность и задачи на взаимное пере­сечение.

Точка принадлежит плоскости, если она принадлежит линии плоскости; прямая ли­ния принадлежит плоскости, если две ее точ­ки принадлежат плоскости.

Точка принадлежит поверхности, если она принадлежит конкретной линии поверх­ности.

Поверхности вращения

Поверхности вращения нашли самое широкое применение в технике. Они огра­ничивают поверхности большинства маши­ностроительных деталей.

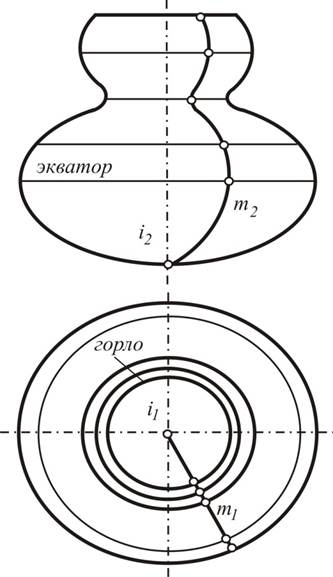
«Зеленую улицу» для их внедрения обеспечила простота форми­рования. Эти поверхности образуются вра­щением криволинейной или прямолинейной образующей m вокруг неподвижной прямой оси i

(рис.1). На чертеже ось поверхности вращения обычно располагают перпендикулярно од­ной плоскости проекций.

Геометрическая часть определителя по­верхности вращения

состоит из этих двух линий: образующей m и оси i. Каждая точка образующей при вра­щении описывает окружность (параллель), плоскость

ко­торой перпендикулярна оси вращения. Так создается каркас поверхности, со­стоящий из множества окружностей. Наименьшую парал­лель называют горлом, наибольшую - эква­тором.

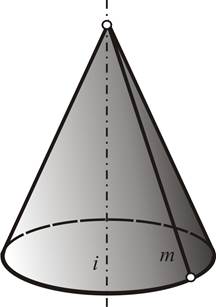
Рис.2. Конус вращения
Рис.1. Поверхность вращения	Рис.3. Цилиндр вращения

Кривые на поверхности вращения, об­разующиеся в результате пересечения по­верхности плоскостями, проходящими через ось вращения,

называются меридианами. Все меридианы одной поверхности конгру­энтны. Фронтальный меридиан называют главным меридианом, он

определяет фрон­тальный очерк поверхности вращения.

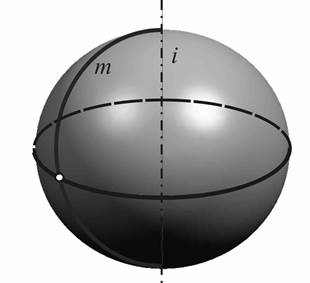
Рис.4. Сфера

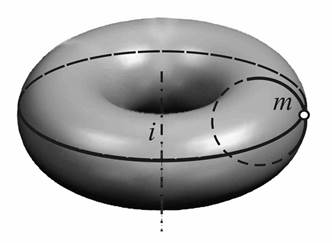
Рис.5. Тор

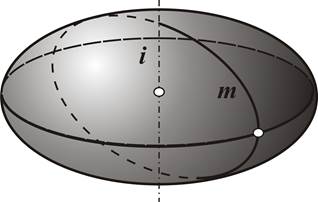
Рис.6. Эллипсоид вращения

Коническая поверхность вращения об­разуется вращением прямой m вокруг пере­секающейся с ней прямой — оси i (рис.2). Эту поверхность называют еще конусом вращения или прямым круговым конусом.

Цилиндрическая поверхность враще­ния образуется вращением прямой m вок­руг параллельной ей оси i (рис.3). Эту поверхность называют еще цилиндром вра­щения или прямым круговым цилиндром.

Сфера образуется вращением окруж­ности m вокруг прямой i (рис.4).

Тор образуется вращением окружности или ее дуги вокруг оси, лежащей в плоскости окружности. Если ось расположена в пределах образующей окружности, то такой тор называется закрытым. Если ось вращения находится вне окружности, то такой тор называется от­крытым (рис.5). Открытый тор назы­вают еще кольцом.

Поверхности вращения могут быть об­разованы и другими кривыми второго по­рядка.

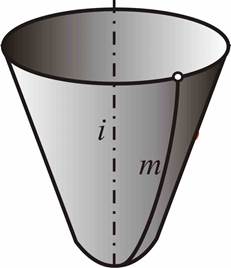
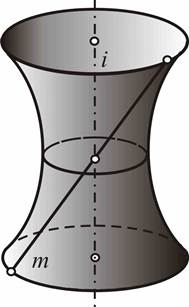
Эллипсоид вращения (рис.6) образуется вращением эллипса вокруг од­ной из его осей; параболоид вращения (рис.7) - вращением параболы вок­руг ее оси; гиперболоид вращения однополостный (рис.8) образуется враще­нием гиперболы вокруг мнимой оси, а двуполостный - вращением гиперболы вокруг действительной оси.

Рис.7. Параболоид вращения	Рис.8. Гиперболоид вращения

Линейчатые поверхности

Линейчатой называют поверхность, которая образуется движением прямой линии (образующей) в пространстве по определённому закону [1].

Линейчатые поверхности с одной направляющей.

Коническая поверхность образуется перемещением прямолинейной образующей l по криволинейной направляющей a. При этом одна точка образующей всегда не­подвижна и является вершиной кони­ческой поверхности (рис.9). Опреде­литель конической поверхности включает вершину S и направляющую a.

Цилиндрическая поверхность образует­ся перемещением прямой l, пересекающей кривую нап­равляющую aи параллельно заданному направлению S (рис.10). Цилиндри­ческую поверхность можно рассматривать как частный случай конической поверхности с бесконечно удаленной вершиной.

Определитель цилиндрической поверх­ности состоит из направляющей aи нап­равления S.

Торсом называется поверхность, обра­зованная перемещением прямолинейной образующей l ,касающейся при своем движении во всех своих положениях некоторой пространст­венной кривой т, называемой ребром воз­врата (рис.11). Ребро возврата пол­ностью задает торс и является геомет­рической частью определителя поверх­ности.

Линейчатые поверхности с плоскостью параллелизма

Поверхности с плоскостью параллелиз­ма представляют собой множество прямых (образующих), параллельных некоторой плоскости (плоскости параллелизма) и пересекающих две данные линии - на­правляющие.

Если направляющими являются две кривые линии, то поверхность называется цилиндроидом. Если одна из направ­ляющих — прямая линия, а вторая — кри­вая, то поверхность называется конои­дом и, наконец, если обе направляю­щие — прямые линии, то поверхность называют гиперболическим пара­болоидом или косой плоскостью.

Поверхность цилиндроида определяется плоскостью параллелизма Σ (рис.12) и двумя криволинейными направляющими a и b, которые могут быть пространствен­ными кривыми или плоскими. В последнем случае

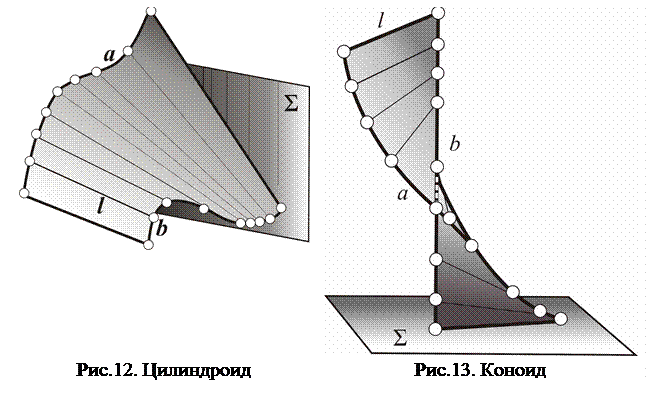плоскости, в которых расположены направляющие, не должны совпадать друг с другом. Прямая линия l, оставаясь параллельной заданной плоскости Σ, при своем движении по направляющим образует поверхность цилиндроида.

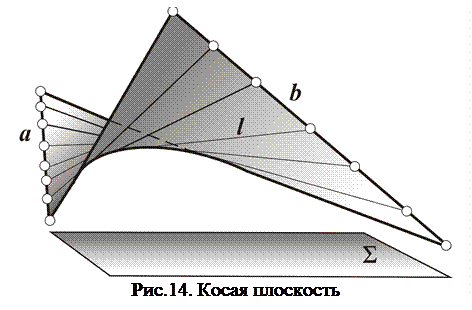
Коноид и гиперболический параболоид отличаются от цилиндроида лишь видом направляющих, которые входят в набор постоянных элементов геометрических час­тей определителей рассматриваемых по­верхностей. У коноида – прямая и кривая (рис.13), а у косой плоскости две прямые (рис.14).

Взаимное пересечение поверхностей

Задачи на взаимное пересечение связа­ны с построением точек, принадлежащих одновременно двум рассматриваемым гео­метрическим образам (прямой и плоскости, двум плоскостям, плоскости и поверхности, двум поверхностям). Каждую из этих об­щих точек строят в пересечении двух вспо­могательных линий. Вспомогательные ли­нии должны быть графически простыми и принадлежать одной вспомогательной по­верхности (плоскости). Выбор вспомога­тельных поверхностей, несущих в себе вспо­могательные линии, зависит от формы пере­секающихся поверхностей. Совокупность построенных общих точек дает линию пере­сечения.

Пересечение поверхности с прямой

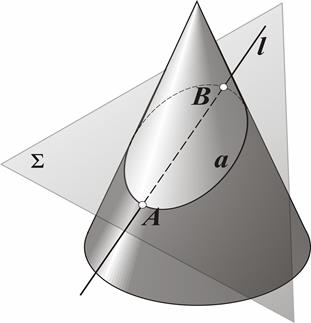
Рис.15. Пересечение поверхности с прямой

Точки пересечения прямой l с поверхностью кругового конусаопределяются с помощью вспомогательной секущей плоскости Σ, проведённой через данную прямую (рис.15). Линия пересечения этой плоскости с конусом a пересекается с прямой в двух точках A и B.

Построение линии пересечения двух поверхностей

Линия пересечения двух поверхностей в общем виде представляет собой про­странственную кривую, которая может распадаться на две части и более. Эти части могут быть и плоскими кривыми. При пересечении гранных поверхностей в общем случае получается пространственная ломаная линия. Обычно линию пересечения двух поверхностей строят по отдельным точкам. Сначала определяют опорные точки в пересечении контурных линий каждой поверхности с другой поверхностью. Опорные точки позволяют видеть, в каких пределах

расположены проекции линии пересечения и где между ними имеет смысл определить промежуточные или случайные точки. При этом нужно иметь в виду, что проекции линии пересечения всегда располагаются в пределах площади наложения одноименных проекций пересекающихся поверхностей.

Общим способом построения точек ли­нии пересечения двух поверхностей являет­ся способ вспомогательных поверхностей. Вспомогательная поверхность пересекает данные поверхности по линиям (желатель­но графически простым). В пересечении этих линий получаются точки, принадлежа­щие обеим поверхностям, т. е. точки их линий пересечения. В качестве вспомога­тельных поверхностей обычно используют или плоскости, или сферы. Отсюда и спосо­бы построения линий пересечения поверх­ностей — способ вспомогательных секущих плоскостей и способ вспомогательных сфер.

Способ вспомогательных секущих плоскостей

Вспомогательные секущие плоскости могут быть общего и частного положения. Плоскости общего положения имеют ограниченное применение. Их удобно использовать при построении ли­ний пересечения конических (пирамидаль­ных) и цилиндрических (призматических) поверхностей общего вида, когда основания этих поверхностей расположены в одной и той же плоскости.

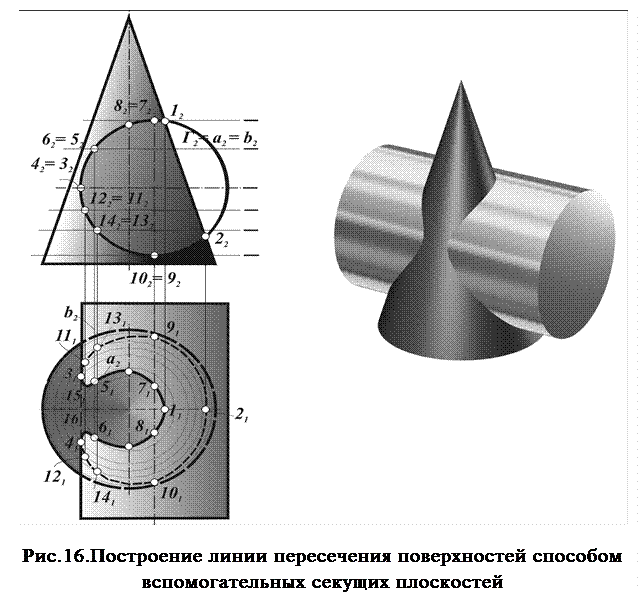
Рассмотрим на примере пересечения ко­нуса вращения с цилиндром вращения построение их линии пересечения методом вспомогатель­ных секущих плоскостей частного положе­ния (рис.16).

Выбирать вспомогательные фронтальные плоскости, параллельные П₂, для построе­ния точек линии пересечения нецелесообразно, так как они будут пересекать конус по гипербо­лам. Графически простые линии a (окружнос­ти параллелей) на данной поверхности по­лучаются от пересечения их горизонтальны­ми плоскостями уровня Г. На цилиндре линии пересечения будут выглядеть прямыми b.

Все так называемые особые точки линии пересечения расположены на очерке цилиндра вращения – точки видимости на плоскости П₁ - 3 и 4, а наивысшие точки 7 и 8, а также наинизшие 9 и 10 на плоскости П₂. Соединяем одноименные проекции пост­роенных точек с учетом их видимости плавными кривыми и получаем проекции искомой линии пересечения.

Так как поверхности в начертательной геометрии являются пустотелыми оболочками, то на фронтальной плоскости П₂ обе поверхности будут видимыми.

Способ вспомогательных секущих концентрических сфер

Способ вспомогательных секущих концентрических сфер возможно использовать при условии, что в пересечении участвуют две поверхности вращения, чьи оси вращения пересекаются. Центр вспомогательных секущих сфер располагается в точке пересечения осей вращения. Сферы следует строить на плоскости, параллельной общей плоскости симметрии поверхностей.

На рис.17 показано пересечение двух конусов враще­ния. Их

оси в своем пересе­чении образуют общую для этих конусов плоскость симметрии, параллель­ную плоскости П_2.

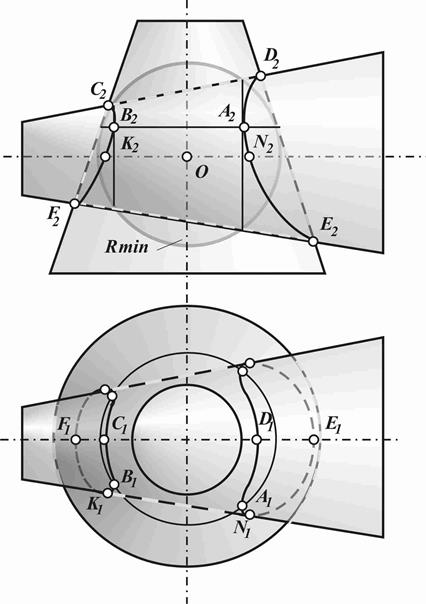Рис.17. Построение линии пересечения поверхностей способом вспомогательных секущих концентрических сфер

В данном случае применены вспомогательные сферы, проводимые из одного и того же центра - точки О пересечения осей конусов. Так, для нахождения точек А и В проведена сфера радиуса Rmin, вписанная в один из конусов и пересекающая другой.

Точки К и N, в которых, на горизонтальной проекции происходит разделение на видимую и невидимую части линии пересечения, определены при помощи плоскости, проходящей через ось конуса. Особые точки C,D,E и F на фронтальной проекции также построены при помощи плоскости, проходящей через ось конуса.