Расчет цепи методом контурных токов.
Метод контурных токов.
Метод контурных токов используется для расчета как резистивных линейных
цепей с постоянными токами, так и комплексных схем замещения линейных
цепей с гармоническими токами.
В расчет вводятся так называемые контурные или фиктивные токи, которые замыкаются в независимых замкнутых контурах. Независимые контуры отличаются друг от друга наличием хотя бы одной новой ветви. Контурные токи принимают за неизвестные, находят сначала их, и уже затем через контурные токи определяют неизвестные токи в ветвях.
Чтобы сократить количество неизвестных, источник тока включают в контур, но только в один. Ток данного контура считают известным и равным току источника. Если в схеме несколько источников тока, число неизвестных можно существенно сократить, включая источники в разные контуры. В таких схемах применение этого метода наиболее рационально.
Число неизвестных в данном методе равно количеству уравнений, которые необходимо составить по второму правилу Кирхгофа для данной схемы. Уравнения составляют только для контуров, не содержащих источников тока.
Основой для расчёта режима работы любой электрической цепи являются законы Ома и правила Кирхгофа. С их помощью, зная параметры элементов электрической цепи можно определить протекающие в ней токи и действующие напряжения. Можно решить обратную задачу по определению параметров цепи, которые обеспечивают требуемые токи и напряжения.
Расчет цепи методом контурных токов.
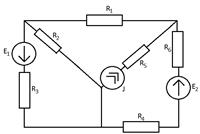
Найти токи в ветвях схемы I1, I2, I3, I4
Дано: R1=5 Ом; R2=10 Ом; R3=10 Ом;R4=3 Ом; R5 =40 Ом; R6=7 Ом;
E1 = 40 В; E2 = 10 В; J = 1 А
| 
|
=
1. Топология.
Определяем общее число ветвей: p*=5.
Определяем число ветвей с источниками тока: pит=1.
Определяем число ветвей с неизвестными токами: p*- pит=4.
Количество узлов q=3.
Определяем необходимое и достаточное число контуров:
M = p*-(q-1) = 5 – (3-1)= 3.
Алгоритм расчета
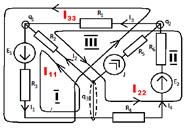
2. Произвольно наносим на схему номера и направления 4-х неизвестных токов I1, I2 , I3, I4..
3. Обозначаем на схеме контура I, II, III и произвольно выбираем направления их обхода и контурные токи в них I11, I22, I33.
4. Записываем выражения для токов в ветвях через контурные токи:
I1=I11+I33, I2=I11- I22, I3= I22+ I33, I4= I22, I5= J
5. Составляем уравнения по второму правилу Кирхгофа для тех контуров, токи в которых неизвестны (для контуров без источника тока):
I1R1 + I2R2 = E1, I3R1 – I2R2 +I4(R4+R6) = E2
6. В этой системе заменяем токи в ветвях выражениями, полученными в пункте 4:
R3(I11 + I33) + R2(I11 – I22) = E1
R1(I22+I33) – R2(I11- I22) + I22(R4+R6) = E2
7. Подставим заданные числовые значения сопротивлений и ЭДС и после приведения подобных получим простую систему уравнений:
2I11 – I22 = 3А, 5I22 - 2I11= 1Аоткуда I11 = 2A, I22 = 1A
8. Подставим эти значения контурных токов в уравнений в п. 4 и окончательно получаем:
I1 = 3A, I2 = 1A, I3 = 2A, I4 = 1A
Дата добавления: 2017-11-21; просмотров: 1444;











