Максимальный электромагнитный момент
Кривая M=f(s) имеет два явно выраженных максимума – один — в генераторном, другой — в двигательном режиме. Для определения Мтах выражение (3.4) дифференцируют по скольжению s и первую производную функции приравнивают нулю, т. е.
dM/ds =0.
В результате получают значение критического скольжения s кр:
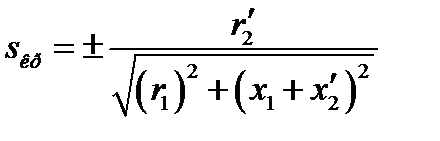 . (3.5)
. (3.5)
Подставив s кр из (3.5) в (3.4), после преобразований получаем максимальный электромагнитный момент:
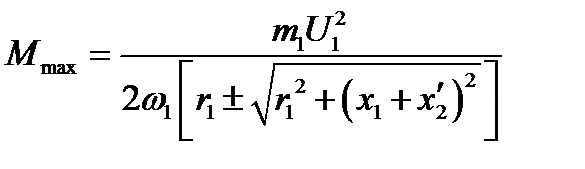 . (3.6)
. (3.6)
Знак плюс в (3.5) и (3.6) относится к двигательному или тормозному режимам работы, знак минус — к генераторному.
Из (3.5) и (3.6) следует, что значения s кр как в двигательном, так и в генераторном режиме одинаковы, а максимальный момент в генераторном режиме больше, чем в двигательном. Обычно из-за малого сопротивления r1 разница в моментах получается небольшой.
Из (3.6) следует, что максимальный момент не зависит от активного сопротивления цепи ротора r2', однако согласно (3.5) это сопротивление оказывает влияние на скольжение s кр, при котором асинхронная машина развивает момент Мтах.
На рис. 3.3 приведены кривые M=f(s) для различных значений r2' при работе машины с s>0. Они показывают, что с увеличением r2' максимум момента смещается в область больших скольжений, сохраняя при этом свое значение.
Рис. 3.3. Зависимости M=f(s) при различных активных сопротивлениях обмотки ротора
I
В соответствии с (3.6) Мтах пропорционален квадрату приложенного к обмотке статора напряжения. Поэтому снижение напряжения может привести к значительному уменьшению кратности максимального момента Мтах и перегрузочной способности двигателя.
В асинхронных машинах активное сопротивление статора r1 в несколько раз меньше индуктивных сопротивлений x1 и х'2 Поэтому для практических целей, полагая r1=0 из (3.5) и (3.6) получим
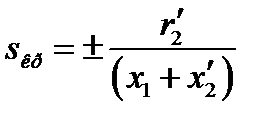 (3.7)
(3.7)
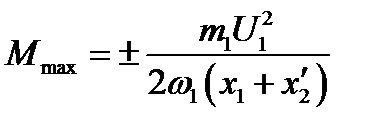 (3.8)
(3.8)
Из (3.8) видно, что максимальный момент обратно пропорционален индуктивным сопротивлениям рассеяния обмоток статора x1 и ротора х'2 Поэтому при проектировании машины для увеличения Мтах в первую очередь следует уменьшать эти сопротивления.
Дата добавления: 2017-11-21; просмотров: 1429;











