Особенности технико-экономических расчетов с учетом расчета надежности

В качестве основного критерия оптимальной надежности СЭС выступает минимум приведенных затрат с учетом ожидаемого ущерба за год от всех значимых отказов работоспособности, в качестве дополнительного критерия – отношение ожидаемого ущерба к приведенным затратам.

В случае, когда в качестве экономической оценки надежности принимаются удельные разовые показатели ущерба конкретных производств, в качестве основных технических показателей надежности выступает время безотказной работы Т, время восстановления Т_в (или обратные им характеристики – параметр потока отказов системы ω_с = Т^-1 , параметр потока восстановления системы µ_с = Т_в^-1) и опасность отказов ρ = λ_с/µ_с = Т_в/Т.

Если в качестве экономической оценки надежности принимаются усредненные для производства удельные разовые показатели ущерба, то в качестве технического показателя выступает вычисляемая по опасности отказа (ρ) величина условного недоотпуска электроэнергии, учитывающая основные факторы отказа работоспособности.

Если при отказе работоспособности системы типа j (например, отключение силового трансформатора, КЗ на одной из питающих линий) отключаются потребители суммарной мощности S_j, кВ·А (или Р_j кВт) на время Т_вj (ч) ω_j раз в году, то величина недоотпущенной электроэнергии ΔW_j равна:

ΔW_j = S_j T_вj ω_j . (4.1)

где T_вj, ω_j - показатели надежности системы для отказа вида j. Вместо них возможно использование комплексного показателя – опасности отказа ρ_j. Тогда величина недоотпущенной электроэнергии равна:

ΔW_j = S_j ρ_j 8760 . (4.2)

Однако, из-за особенностей расчета надежности подобная оценка недоотпуска не всегда точна. Особенность заключается в том, что при расчете надежности находятся вероятностные характеристики сформулированного отказа и всех более тяжелых отказов системы. Так, если отказ системы – погашение одного трансформатора из трех, то в показателях надежности учитывается погашение также и двух и трех трансформаторов, тогда как для подсчета недоотпуска требуется оценить погашение только одного трансформатора.

Рассмотрим способы оценки величины ущерба от недоотпуска электроэнергии с учетом показателей надежности системы электроснабжения. На рисунке 4.1 представлена структурная схема системы электроснабжения.

Рис. 4.1. Структурная схема системы электроснабжения

Элементы схемы:

1 – генератор; 2,3 – трансформаторы; 4,5,6,7 – линии электропередач; 8 – потребитель.

Пропускные способности элементов 2,3 – 0,5 о.е., 4-7 – 0,25 о.е. Под отказом работоспособности подразумевают ограничение электроснабжения на величину ΔS = 0,25 о.е. Для решения используем функцию алгебры логики, называемую «или, но не и» и обозначаемую символом . Эта операция вводится для тех конъюнкций, совместное возникновение которых недопустимо, так как не отвечает формулировке состояния отказа. Вероятность отказа 1 или 2 элемента (но не двух одновременно), то есть вероятностный полином такой функции для двух событий равен:

Q(1 2) = Q(1· + 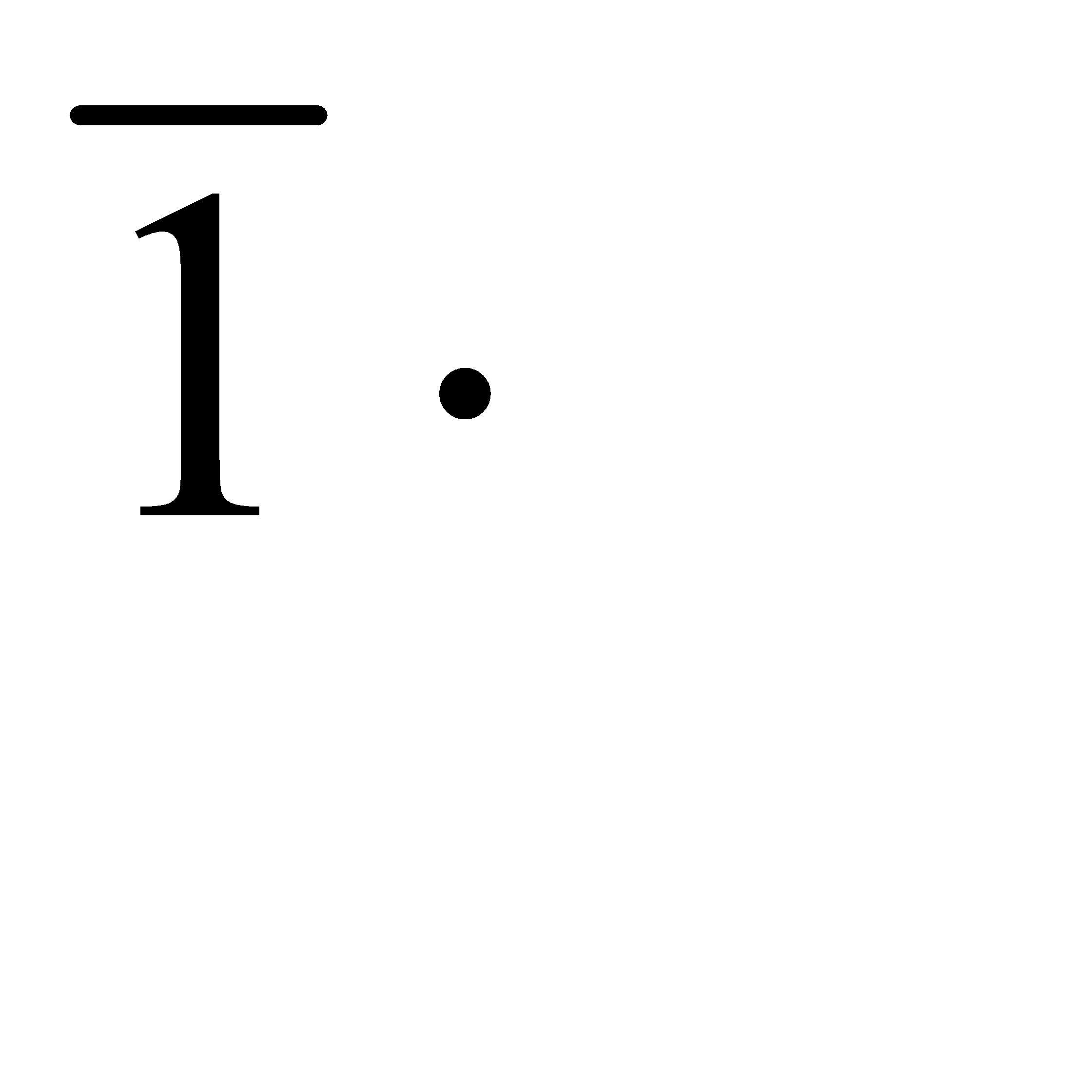2) = q₁ + q₂ – 2q₁q₂.

Для числа событий больше двух :

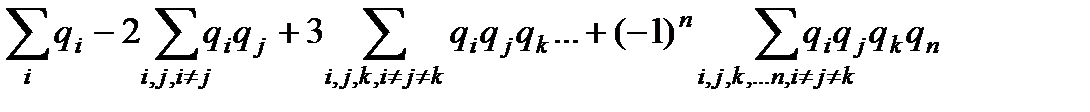Q(1 2 2 … n) = (4.3)

В рассматриваемой системе электроснабжения к заданному отказу приводят одиночные отказы линий электропередач. Одиночные отказы других элементов и сочетания отказов не должны присутствовать в логической функции. Логическая функция работоспособности 1, 2 и 3 элемента схемы при отказе 4 ИЛИ 5 ИЛИ 6 ИЛИ 7 элемента записывается в виде .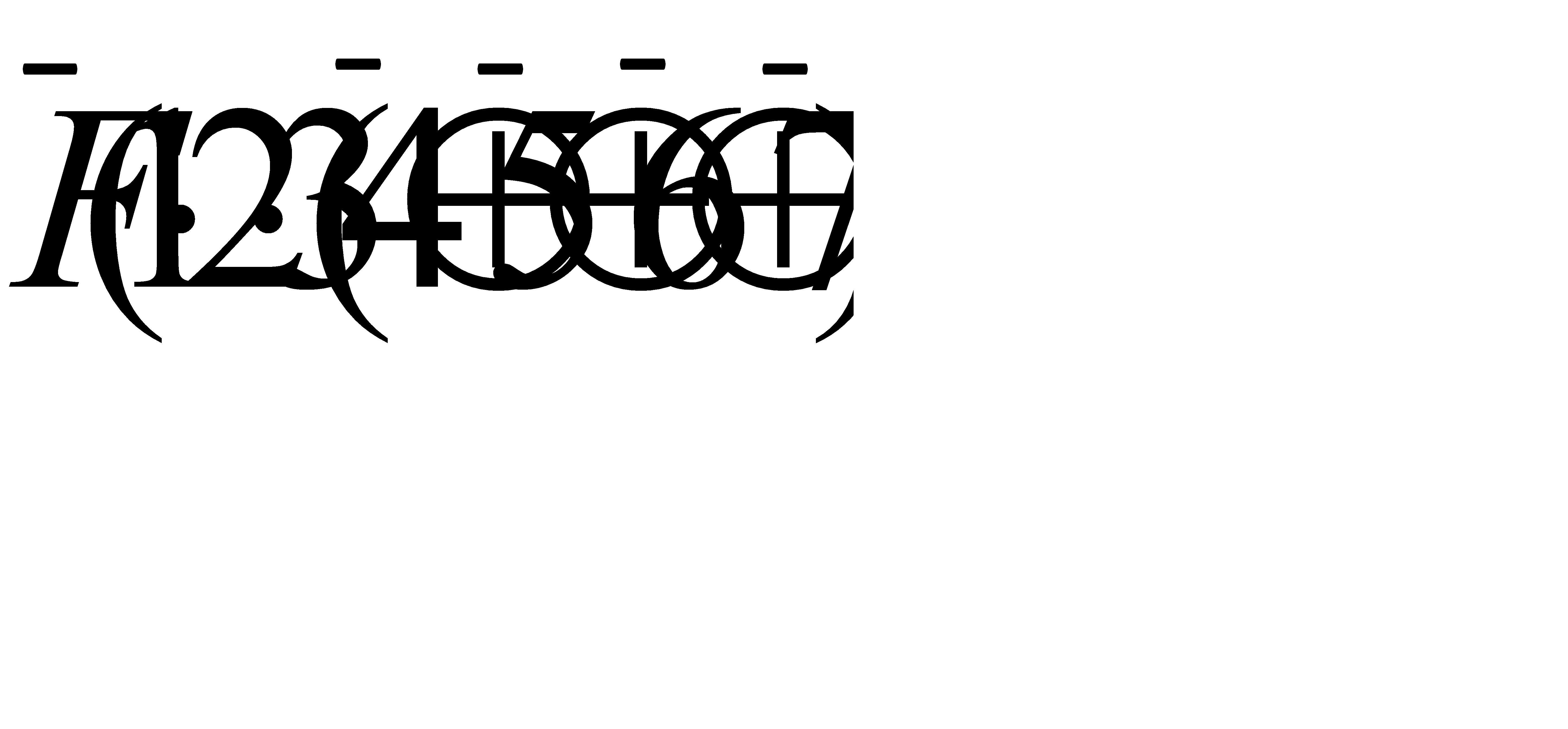

Вероятность отказа системы электроснабжения при такой логической функции равна:

Q( 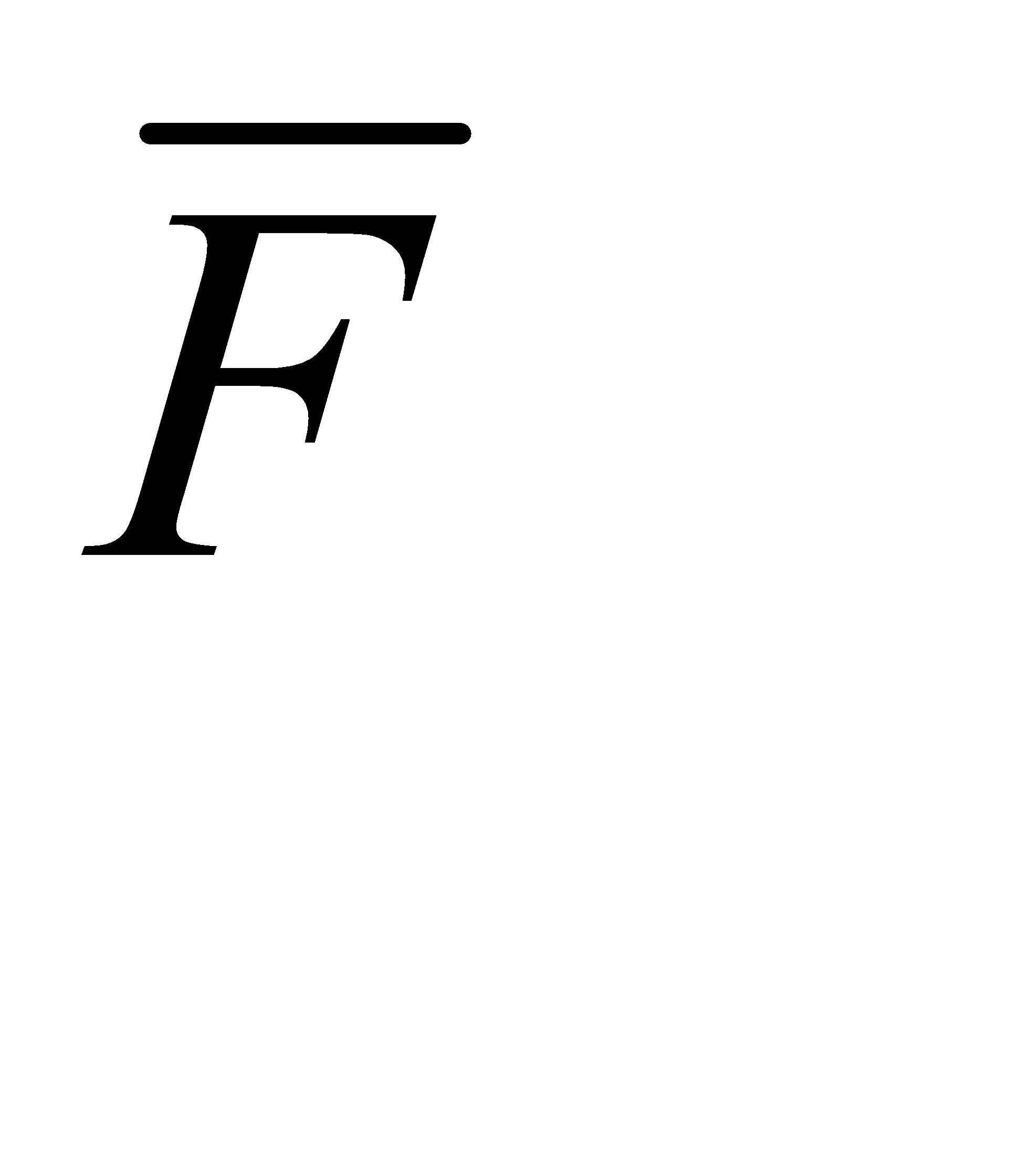) = p₁p₂p₃[(q₄+q₅+q₆+q₇) – (2 (q₄q₅+q₄q₇+q₁q₆+q₅q₆+q₆q₇) + 3(q₄q₅q₆+q₄q₅q₇+q₄q₆q₇+q₅q₆q₇) – 4(q₄q₅q₆q₇)] .

При условии, что все элементы имеют одинаковые показатели надежности , выражение упрощается

Q( 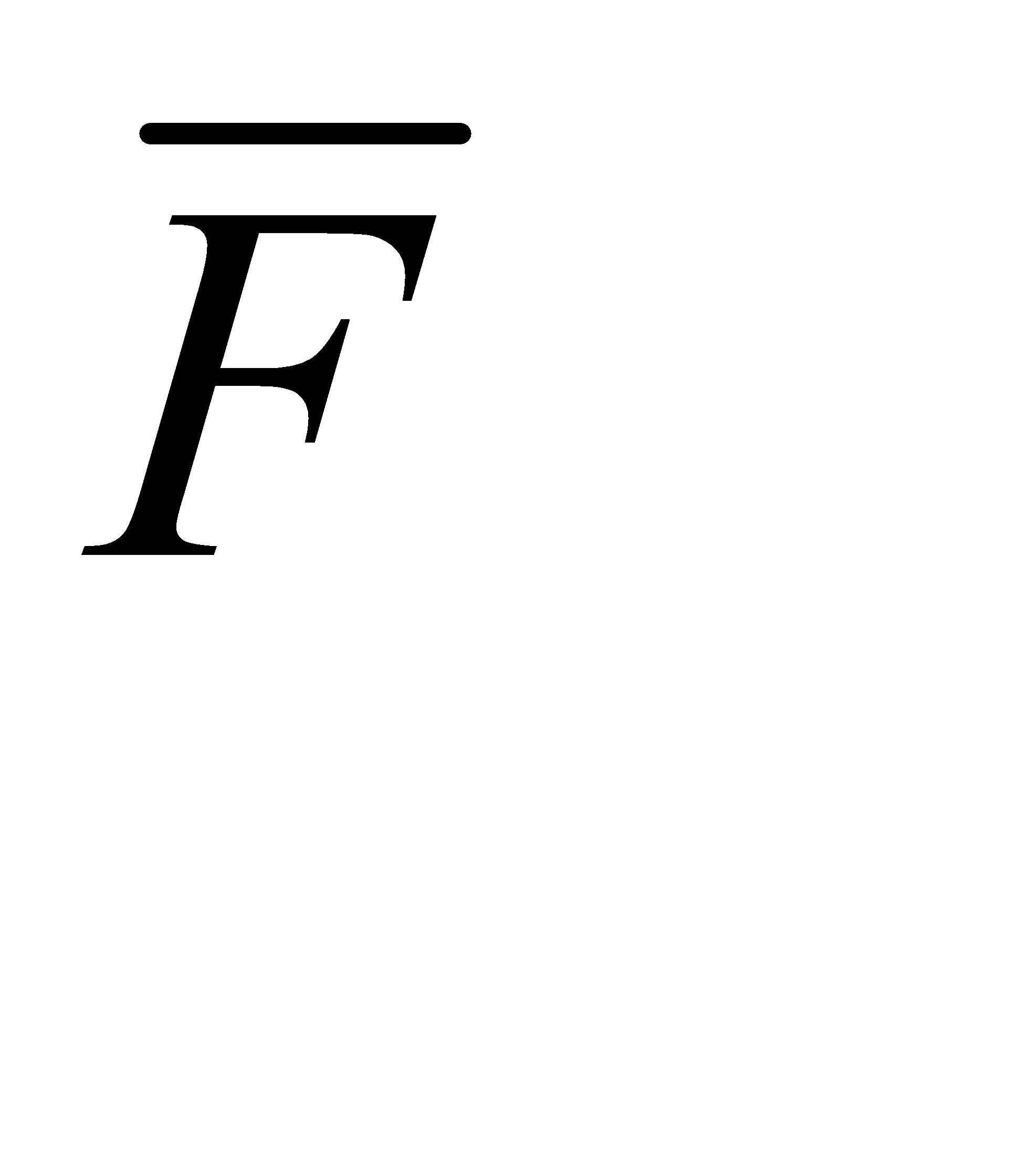) = 4q – 24q²+60q³-80q⁴+60q⁵-24q⁶+4q⁷.

Определим вероятность отказа этой же системы электроснабжения с помощью обычных функций логики (конъюнкции и дизъюнкции).

;

Q( 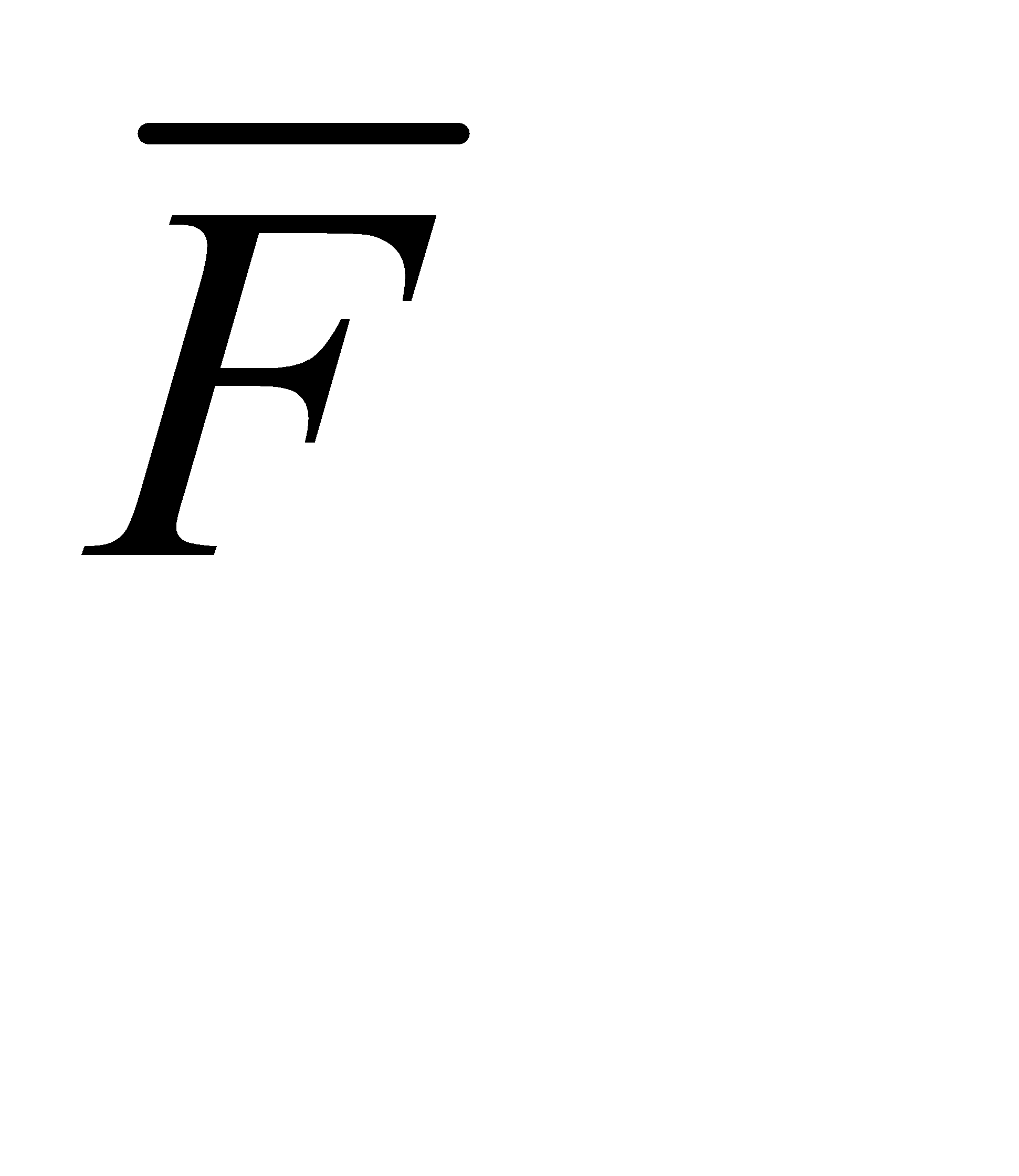) = 4q-6q²+4q³-q⁴.

Вероятность получается завышенной (приблизительно на 24q² – 6q² = 18q²). Погрешность возникает за счет наложения отказов линий и за счет неучета работы других элементов системы. Способ расчета вероятности отказа системы электроснабжения при помощи функции алгебры логики конъюнкции и дизъюнкции рекомендуется для систем с q_i<<1.