ОПРЕДЕЛИТЕЛИ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКОВ. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ.
Тема 1. Системы линейных уравнений
Система уравнений называется линейной, если все уравнения, входящие в систему, являются уравнениями первой степени относительно переменных. Если система из n линейных уравнений содержит n неизвестных, то возможны следующие три случая:
1) система не имеет решений;
2) система имеет единственное решение;
3) система имеет бесконечно много решений.
Рассмотрим решение систем линейных уравнений с помощью определителей.
1. Система двух линейных уравнений с двумя неизвестными
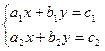 . (1)
. (1)
имеет единственное решение, которое вычисляется по формулам Крамера:
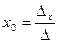 ,
, 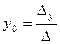
при условии, что 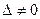 . Числа
. Числа 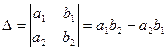 ,
, 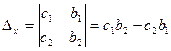 и
и 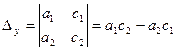 называются определителями второго порядка.
называются определителями второго порядка.
Пример. Решите с помощью определителей систему 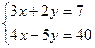 .
.
Решение. Вычисляем определители: 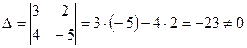 ;
;
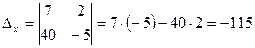 ;
; 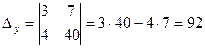 .
.
Тогда по формулам Крамера получаем:
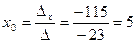 ;
; 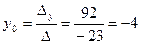 .
.
Ответ: (5;-4).
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
Рассмотрим свойства определителей на примере определителей второго порядка:
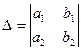 .
.
Числа 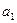 ,
, 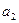 ,
, 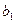 ,
, 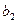 называются элементами определителя. Определитель второго порядка равен разности между произведением его элементов, стоящих на главной диагонали (идущей слева направо вниз) и произведением элементов, стоящих на второй диагонали.
называются элементами определителя. Определитель второго порядка равен разности между произведением его элементов, стоящих на главной диагонали (идущей слева направо вниз) и произведением элементов, стоящих на второй диагонали.
Свойства определителей
1. Величина определителя не изменится от замены строк столбцами:
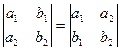 .
.
2. Величина определителя от перестановки любых двух параллельных его рядов меняет знак на противоположный:
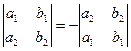 ;
; 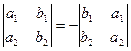 .
.
3. Определитель равен нулю, если оба элемента какой-либо строки или столбца равны нулю:
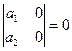 ;
; 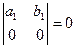 .
.
4. Определитель равен нулю, если в нём пропорциональны (или равны) соответствующие элементы его строк или столбцов:
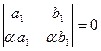 ;
; 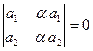 ;
; 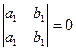 ;
; 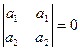 .
.
Пример: 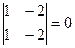 ;
; 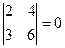 .
.
5. Чтобы умножить определитель на произвольный множитель, достаточно на него умножить элементы одной какой-либо строки или одного какого-либо столбца определителя: 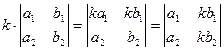 .
.
Таким образом, общий множитель элементов одного ряда можно выносить за знак определителя.
Пример: 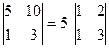 .
.
6. Величина определителя не изменится, если к элементам одного ряда прибавить элементы параллельного ряда, умноженные на одно и то же число:
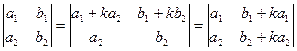 .
.
2. Рассмотрим систему трёх линейных уравнений с тремя неизвестными:
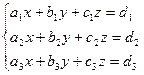 (2)
(2)
при условии, что определитель системы
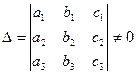 .
.
В этом случае система (2) имеет единственное решение, которое вычисляется по формулам Крамера: 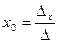 ;
; 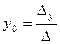 ;
; 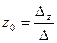 ,
,
где 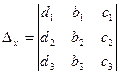 ;
; 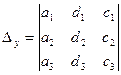 ;
; 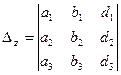 .
.
Определитель третьего порядка 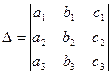 можно вычислять по формуле, которая называется формулой разложения определителя третьего порядка по элементам первой строки:
можно вычислять по формуле, которая называется формулой разложения определителя третьего порядка по элементам первой строки:
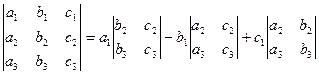 .
.
Пример: Вычислить определитель 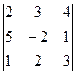 .
.
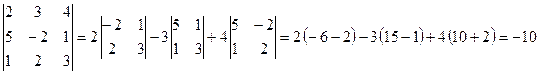 .
.
Свойства 1-6 определителей второго порядка распространяются также на определители третьего порядка.
Пример. Решите систему 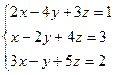 .
.
Решение. Вычисляем определители:
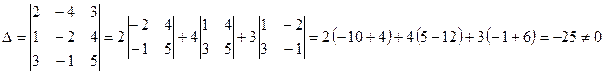 ;
;
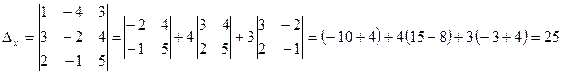 ;
;
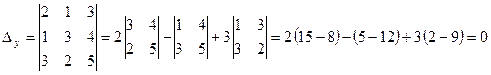 ;
;
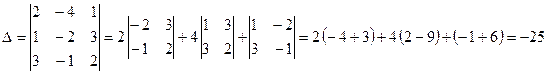 .
.
По формулам Крамера получаем:
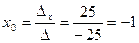 ;
; 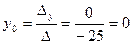 ;
; 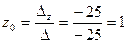 .
.
Ответ: (-1;0;1).
Если в системе (2) определитель 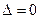 , то возможны следующие случаи:
, то возможны следующие случаи:
I. Элементы двух строк определителя 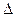 пропорциональны, например,
пропорциональны, например,
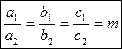 .
.
Тогда: 1) если 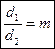 , то система неопределённа;
, то система неопределённа;
2) если 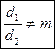 , то система несовместна.
, то система несовместна.
Пример: Решите систему 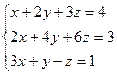 .
.
Определитель системы 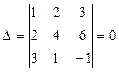 , при этом элементы двух строк определителя пропорциональны:
, при этом элементы двух строк определителя пропорциональны: 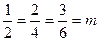 , но
, но 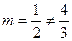 . Тогда данная система несовместна.
. Тогда данная система несовместна.
II. В определителе  нет строк с пропорциональными элементами. Тогда существуют отличные от нуля числа m и n, такие, что
нет строк с пропорциональными элементами. Тогда существуют отличные от нуля числа m и n, такие, что 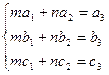 .
.
1) если 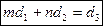 , то система неопределённа;
, то система неопределённа;
2) если 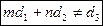 , то система несовместна.
, то система несовместна.
В заключение рассмотрим решение системы трёх линейных однородных уравнений с тремя неизвестными: 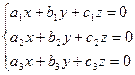 . (3)
. (3)
Система (3) имеет отличные от нуля решения тогда и только тогда, когда определитель системы 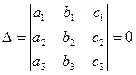 .
.
Пример: Решите систему 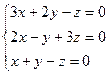 .
.
Вычисляем определитель системы:
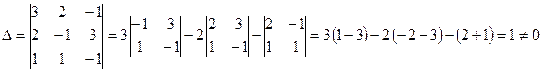 .
.
Следовательно, система имеет единственное решение 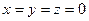 .
.
Тема 2. Матрицы и действия над ними. Основные определения
Определение 1. Матрицей называется таблица чисел aik вида: 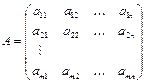 , состоящая из m строк и n столбцов. Числа aik называются её элементами. Это прямоугольная матрица. В частности, если m=1, n>1, получаем матрицу-строку
, состоящая из m строк и n столбцов. Числа aik называются её элементами. Это прямоугольная матрица. В частности, если m=1, n>1, получаем матрицу-строку 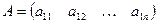 , а если m>1, n=1, матрицу-столбец:
, а если m>1, n=1, матрицу-столбец: 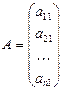 .
.
Определение 2. Матрица 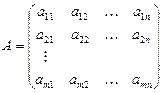 называется невырожденной (неособой), если её определитель
называется невырожденной (неособой), если её определитель 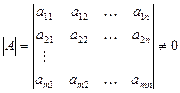 и вырожденной (особой), если
и вырожденной (особой), если 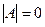 .
.
Определение 3. Матрица называется квадратной, если m=n (n – порядок матрицы). В частности, матрица 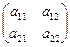 называется квадратной матрицей второго порядка, а матрица
называется квадратной матрицей второго порядка, а матрица 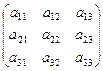 - квадратной матрицей третьего порядка.
- квадратной матрицей третьего порядка.
Определение 4. Квадратная матрица называется диагональной, если все элементы, стоящие вне главной диагонали равны нулю: aij =0 i¹j.
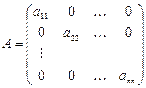
В частности, диагональная матрица, у которой все диагональные элементы равны единице называется единичной. 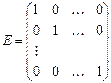
Определение 5. Нулевой матрицей называется матрица, все элементы которой равны нулю: 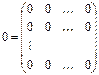
Действия над матрицами
Определение 1. Две матрицы A и B называются равными, если они одинакового размера (т.е. имеют одинаковое число строк и одинаковое число столбцов) и их соответствующие элементы равны. В частности, если
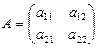 и
и 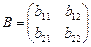
и A=B, то a11=b11, a12=b12, a21=b21, a22=b22.
Матрицы одинакового размера можно складывать и вычитать.
Определение 2. Суммой двух матриц A и B называется матрица С, элементы которой равны сумме соответствующих элементов матриц A и B (обозначение C=A+B). В частности, для квадратных матриц второго порядка получаем:
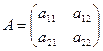 ,
, 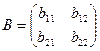 ,
, 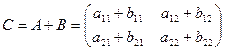 .
.
Пример. Найдите сумму матриц 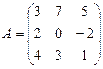 и
и 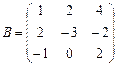 .
.
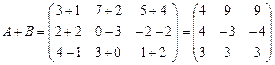
Сумма нулевой матрицы и любой матрицы A даёт матрицу A: A+0 = A.
Определение 3. Разностью двух матриц A и B называется матрица С, элементы которой равны разности соответствующих элементов матриц A и B (обозначение C=A+B).
Пример. Найдите разность матриц 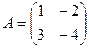 и
и 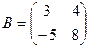 .
.
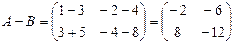 .
.
Определение 4. Произведение матрицы A на число a называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число a.
Пример. Найдите матрицу 3A+5B, если 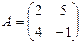 ,
, 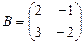 .
.
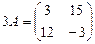 ,
, 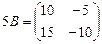 ,
, 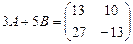 .
.
Определение 5. Произведение матриц А×В определено в том и только в том случае, если число столбцов матрицы А равно числу строк матрицы В. Произведение матрицы А размера m´k на матрицу B размера k´n называется матрица C=A×B размера m´n, элементы которой определяются по формуле: 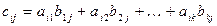
Данная сумма представляет собой сумму произведений соответствующих элементов строки i матрицы А и столбца j матрицы В.
Рассмотрим правило умножения квадратных матриц второго порядка. Пусть даны две матрицы: 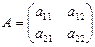 и
и 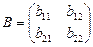 .
.
Произведением матрицы A на матрицу B называется матрица C=AB, равная:
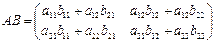 .
.
Пример. Найдите произведение A·B и B·A матриц 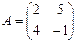 и
и 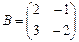 .
.
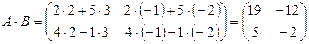
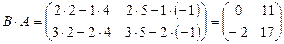
Пример. 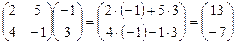
По отношению к произведению двух матриц переместительный закон не выполняется, т.е. A·B ≠ B·A.
Произведение единичной матрицы и любой матрицы A даёт матрицу A: EA = AE=A.
Определение 6. Матрица AT полученная из матрицы А заменой строк столбцами, называется транспонированной.
Пример. 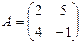 ,
, 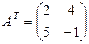 .
.
Обратная матрица
Определение 1. Пусть A – квадратная матрица n–го порядка, а E – единичная матрица того же порядка. Матрица A–1 называется обратной по отношению к матрице A, если выполняются равенства: A×A–1= A–1×A=E.
Определение 2. Минором какого-либо элемента определителя называется определитель, полученный из данного вычёркиванием той строки и того столбца, которым принадлежит этот элемент. Минор элемента aik определителя 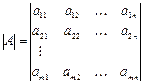 обозначается Mik.
обозначается Mik.
Пример. Минор M12 определителя 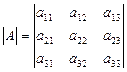 равен
равен 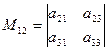 .
.
Определение 3. Алгебраическим дополнением Aik элемента aik определителя 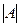 называется его минор Mik, взятый со знаком
называется его минор Mik, взятый со знаком 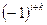 . Следовательно,
. Следовательно, 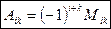 .
.
Пример. Алгебраическое дополнение A12 определителя 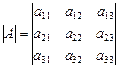 равно
равно 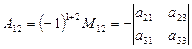 .
.
Теорема. Матрица 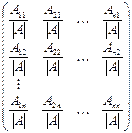 , где Aik – алгебраическое дополнение элемента aik невырожденной матрицы A, является обратной для A. Для матрицы
, где Aik – алгебраическое дополнение элемента aik невырожденной матрицы A, является обратной для A. Для матрицы 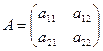 обратной является матрица
обратной является матрица 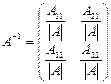 .
.
Пример. Дана матрица 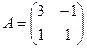 . Найдите обратную матрицу.
. Найдите обратную матрицу.
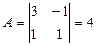 ,
, 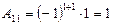 ,
, 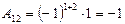 ,
, 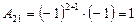 ,
, 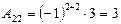 .
.
Тогда 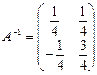 . Сделаем проверку:
. Сделаем проверку: 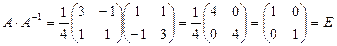 .
.
Исследование системы линейных уравнений.
Решение систем линейных уравнений с помощью обратной матрицы
Рассмотрим случай, когда число уравнений равно числу неизвестных. Пусть дана алгебраическая система n уравнений с n неизвестными:
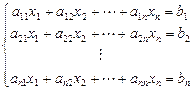
или в матричной форме А×Х=В, где 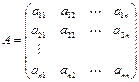 ,
, 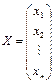 ,
, 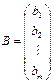 .
.
Если матрица A невырожденная (определитель 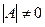 ), т.е. существует обратная по отношению к ней матрица А–1, то решение системы алгебраических линейных уравнений находится по формуле: Х= А–1×В.
), т.е. существует обратная по отношению к ней матрица А–1, то решение системы алгебраических линейных уравнений находится по формуле: Х= А–1×В.
Пример. Решите систему уравнений 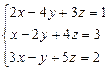 .
.
Перепишем систему в виде A·X=B, где 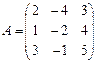 ,
, 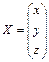 ,
, 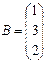 . Решение системы имеет вид Х= А–1×В. Найдём обратную матрицу по формуле
. Решение системы имеет вид Х= А–1×В. Найдём обратную матрицу по формуле 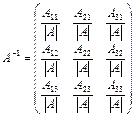 , где Aik – алгебраическое дополнение элемента aik матрицы A. Вычисляем определитель
, где Aik – алгебраическое дополнение элемента aik матрицы A. Вычисляем определитель 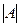 :
:
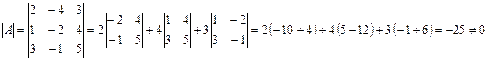 .
.
Находим алгебраические дополнения этого определителя: 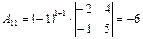 ,
, 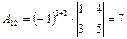 ,
, 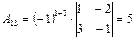 ,
, 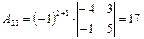 ,
,  ,
, 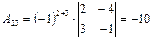 ,
, 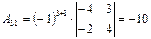 ,
, 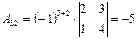 ,
, 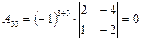 .
.
Следовательно, 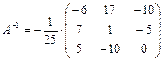 .
.
Получаем решение системы: 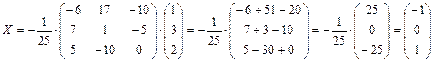 .
.
Ответ: x=-1, y=0, z=1.
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
ЛЕКЦИЯ 2: «ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. ОПЕРАЦИИ НАД ВЕКТОРАМИ»
Основные определения.
Определение 1. Скалярная величина – это величина, которая определяется только своим числовым значением.
Примеры: длина, площадь, объём, масса.
Определение 2. Векторная величина – это величина, которая определяется не только своим числовым значением, но и направлением в пространстве.
Примеры: скорость, ускорение, сила
 Геометрически векторную величину определяют с помощью направленного отрезка, который называется вектором.
Геометрически векторную величину определяют с помощью направленного отрезка, который называется вектором.
Вектор обозначают 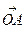 , через
, через 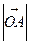 обозначается длина вектора
обозначается длина вектора 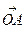 . Для обозначения векторов используются также следующие символы
. Для обозначения векторов используются также следующие символы  ,
,  ,
, 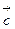 .
.
Определение 3. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 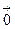 .
.
Определение 4. Два вектора называются равными, если они имеют одинаковые длины и направления.
Определение 5. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.
Определение 6. Два вектора называются противоположными, если они коллинеарны, длины их равны, а направления противоположны.
Вектор, противоположный вектору  , обозначается
, обозначается 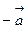 .
.
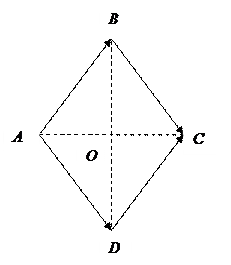 Пример:
Пример:
ABCD – ромб;
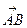 и
и 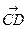 – коллинеарные векторы;
– коллинеарные векторы;
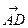 и
и 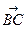 – коллинеарные векторы;
– коллинеарные векторы;
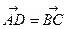 ;
;
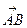 и
и 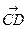 – противоположные векторы.
– противоположные векторы.
Определение 7. Векторы в пространстве называются компланарными, если при откладывании из одной точки они лежат в одной и той же плоскости.
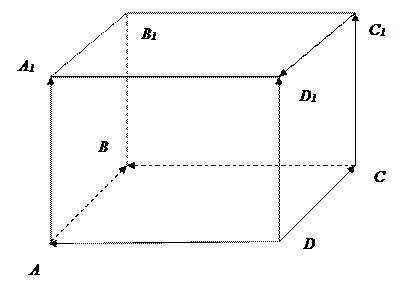
Пример:
ABCDA1B1C1D1 - прямоугольный параллелепипед;
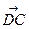 ,
, 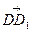 ,
, 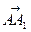 ,
, 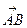 ,
, 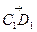 ,
,  - компланарные векторы;
- компланарные векторы;
 и
и  - компланарные векторы.
- компланарные векторы.
Угол между векторами. Проекция вектора на ось
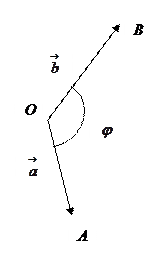
Определение 1. Пусть заданы два вектора  и
и  , где
, где 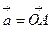 ,
, 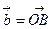 . Тогда величина внутреннего угла
. Тогда величина внутреннего угла 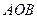 треугольника
треугольника 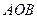 называется углом между векторами
называется углом между векторами  и
и  и обозначается
и обозначается 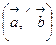 или буквами
или буквами 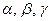 и т.д.
и т.д.
 По определению угол между векторами лежит в промежутке от
По определению угол между векторами лежит в промежутке от 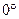 до
до 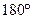 .
.
Определение 2. Если угол между двумя векторами равен 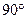 , то эти векторы называются ортогональными или перпендикулярными (обозначение:
, то эти векторы называются ортогональными или перпендикулярными (обозначение: 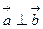 ).
).
Определение 3. Ось – это прямая, на которой выбраны начало отсчёта, положительное направление и единица длины.
Положительное направление и единицу длины на оси можно задать с помощью единичного вектора оси, т.е. вектора, длина которого равна единице. Обозначим его через 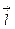 .
.
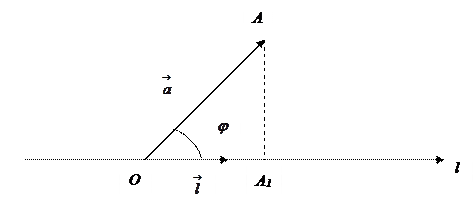
Определение 4. Проекцией вектора  на ось
на ось 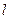 называется число, равное произведению длины этого вектора на косинус угла между вектором
называется число, равное произведению длины этого вектора на косинус угла между вектором  и осью
и осью 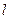 :
: 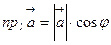 .
.
Рассмотрим три случая:
1) угол 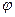 – острый:
– острый:
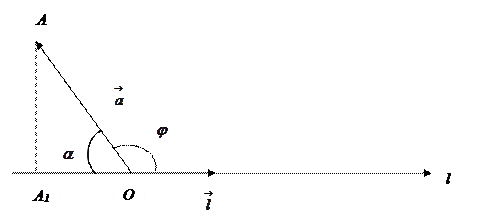
2) угол  - тупой:
- тупой:
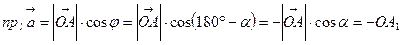
3) угол 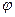 - прямой, т.е.
- прямой, т.е. 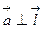 , отсюда
, отсюда 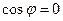 и
и 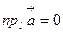 .
.
Операции над векторами
(сложение, вычитание, умножение на число)
Определение 1. Сумма двух векторов – это третий вектор, получаемый: 1) по правилу треугольника; 2) по правилу параллелограмма.
Правило треугольника: начало второго вектора надо перенести в конец первого вектора, вектор суммы при этом равен вектору, идущему из начала первого вектора в конец второго.

Правило параллелограмма: слагаемые векторы необходимо привести к общему началу. Сумма – вектор, идущий по диагонали параллелограмма из общего начала.
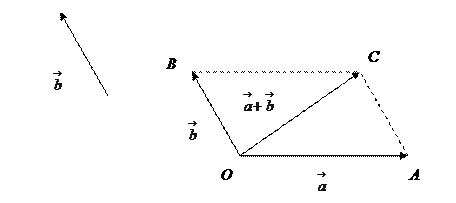
Свойства операции сложения
1) Переместительное свойство или коммутативность: 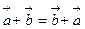 .
.
2) Сочетательное свойство или ассоциативность: 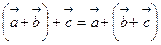 .
.
Определение 2. Для любых векторов  и
и  сумма
сумма 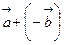 называется их разностью и обозначается
называется их разностью и обозначается 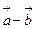 . Здесь
. Здесь 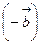 – вектор, противоположный вектору
– вектор, противоположный вектору  .
.
Чтобы произвести вычитание из вектора  вектора
вектора  их необходимо привести к общему началу; вектор, соединяющий их концы и направленный в конец уменьшаемого вектора является вектором разности
их необходимо привести к общему началу; вектор, соединяющий их концы и направленный в конец уменьшаемого вектора является вектором разности 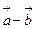 .
.
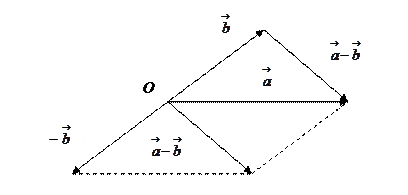
Определение 3. Произведением вектора  на число
на число 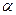 называется новый вектор
называется новый вектор  , коллинеарный первоначальному, причём:
, коллинеарный первоначальному, причём:
1) сонаправленный ему, если число 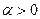 , т.е.
, т.е. 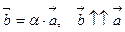 ;
;
2) противоположно направленный, если 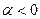 , т.е.
, т.е. 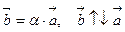 ;
;
3) если 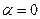 , то
, то 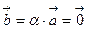 .
.
Для вектора  :
: 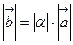 .
.
Свойства операции умножения вектора на число
1) 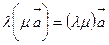
2) 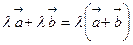
3) 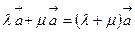
Пример: Построить векторы  ,
, 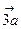 ,
, 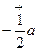 .
.
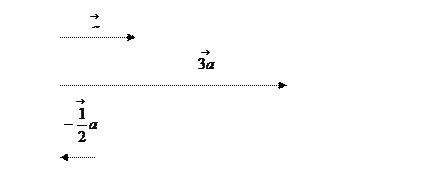
ЛЕКЦИЯ 3: «ПРЯМОУГОЛЬНАЯ ДЕКАРТОВА СИСТЕМА КООРДИНАТ. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ»
Прямоугольная декартова система координат на плоскости
Её образуют две взаимно перпендикулярные оси на плоскости с общим началом: ось 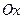 – ось абсцисс и ось
– ось абсцисс и ось 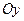 – ось ординат. Единичные векторы этих осей обозначаются
– ось ординат. Единичные векторы этих осей обозначаются 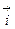 и
и 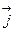
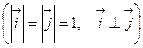 .
.
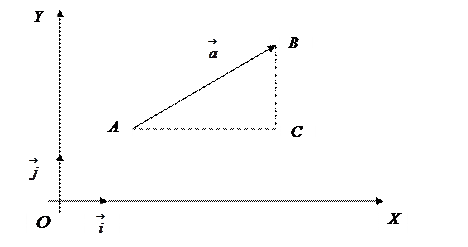
Определение. Проекции вектора на оси координат называют координатами вектора.
Обозначим проекции вектора  через
через 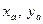 , тогда
, тогда
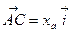 ,
, 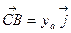
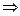
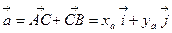 .
.
Последнее равенство часто записывают в виде 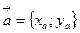 .
.
Прямоугольная декартова система координат в пространстве
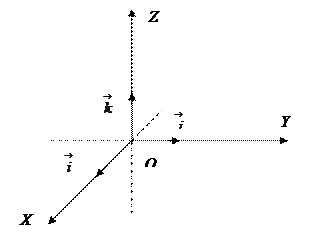 Образована тремя взаимно перпендикулярными осями с общим началом: осью
Образована тремя взаимно перпендикулярными осями с общим началом: осью 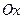 – осью абсцисс, осью
– осью абсцисс, осью 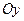 – осью ординат, осью
– осью ординат, осью 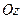 - осью аппликат. Единичные векторы осей
- осью аппликат. Единичные векторы осей 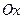 ,
, 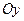 ,
, 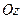 обозначаются
обозначаются 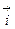 ,
, 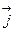 ,
, 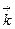 .
.
Определение. Координатами вектора в пространстве называют его проекции на оси координат.
Если в пространстве задан вектор  с координатами
с координатами 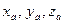 , то справедливо равенство
, то справедливо равенство 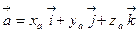 ,
,
которое часто записывают в виде 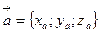 .
.
Координаты суммы, разности векторов и произведения вектора на число
Пусть 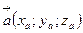 ,
, 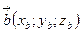 тогда
тогда
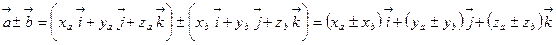 ,
,
т.е. 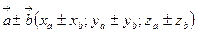 .
.
Аналогично, 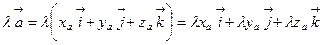 ,
,
т.е. 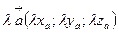 .
.
Следовательно, при сложении (вычитании) двух векторов их соответственные координаты складываются (вычитаются). При умножении вектора на число его координаты умножаются на это число.
Координаты точки
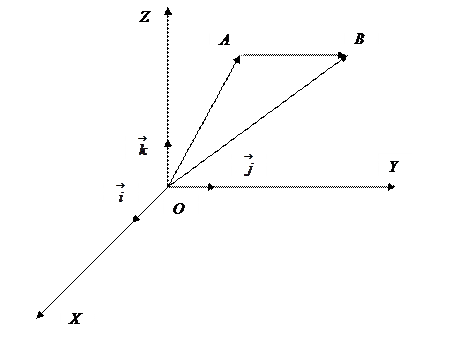
Определение. Вектор, соединяющий начало координат и заданную фиксированную точку  будем называть радиусом – вектором точки
будем называть радиусом – вектором точки  . Координатами точки
. Координатами точки 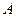 будут координаты радиуса – вектора
будут координаты радиуса – вектора 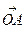 .
.
Пусть 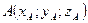 ,
, 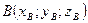 , тогда
, тогда 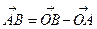
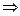
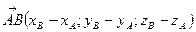 .
.
Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала.
Пример: Найти координаты вектора 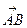 , если
, если 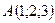 ,
, 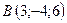 .
.
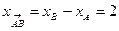 ,
, 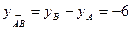 ,
, 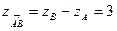 ,
, 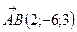 .
.
Скалярное произведение двух векторов
Определение. Скалярным произведением двух векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла между ними (обозначается
называется число, равное произведению длин этих векторов на косинус угла между ними (обозначается 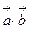 или
или 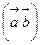 ):
): 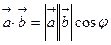 .
.
Пример: Известно, что 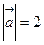 ,
, 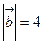 , а угол
, а угол 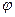 между векторами
между векторами  и
и  равен
равен 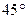 . Найти
. Найти 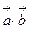 .
.
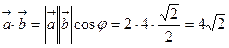
Свойства скалярного произведения
1) 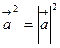
2) Переместительное свойство: 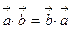
3) Распределительное свойство: 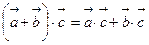
4) 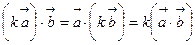
5) 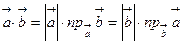
6) Если 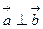 , то
, то 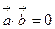
Скалярное произведение векторов, заданных своими координатами
Пусть 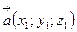 ,
, 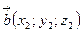 , т.е.
, т.е. 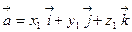 ,
, 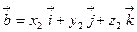 . Тогда
. Тогда
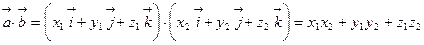 ,
,
так как 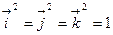 ,
, 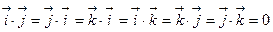 .
.
Получаем
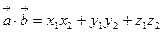 (1)
(1)
Пусть в формуле (1) 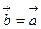 , тогда
, тогда 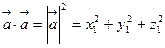 . Следовательно,
. Следовательно,
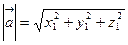 , (2)
, (2)
т.е. модуль вектора равен корню квадратному из суммы квадратов его координат.
Тогда 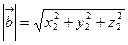 . По определению скалярного произведения
. По определению скалярного произведения
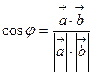 ,
,
отсюда следует 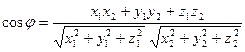 . (3)
. (3)
Пример: Определить угол между векторами 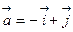 и
и 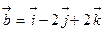 .
.
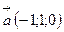 ,
, 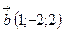
По формуле (3) 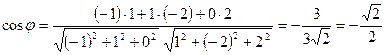 , тогда
, тогда 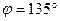 .
.
Из формулы (2) следует, что если заданы точки 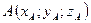 ,
, 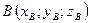 , то
, то 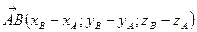 , откуда
, откуда
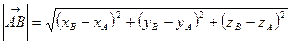 .
.
Условия коллинеарности и перпендикулярности векторов
1) Пусть вектор 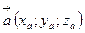 коллинеарен вектору
коллинеарен вектору 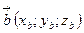 , тогда
, тогда 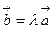 . Для координат векторов
. Для координат векторов  и
и  выполняются следующие условия
выполняются следующие условия
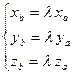
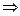
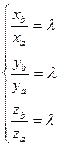
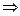
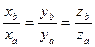 (4)
(4)
Формула (4) определяет условие коллинеарности векторов  и
и  .
.
Пример: Найти произведение 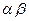 при условии, что векторы
при условии, что векторы 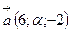 и
и 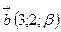 коллинеарны.
коллинеарны.
По формуле (4) получаем: 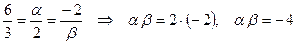 .
.
2) Пусть вектор  перпендикулярен вектору
перпендикулярен вектору 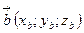 , тогда
, тогда 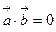 . По формуле (1) получаем:
. По формуле (1) получаем:
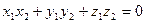 (5)
(5)
Формула (5) определяет условие перпендикулярности векторов  и
и  .
.
Пример: Найти значение 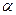 , если векторы
, если векторы 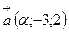 и
и 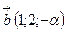 взаимно перпендикулярны.
взаимно перпендикулярны.
По формуле (5) получаем 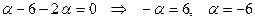 .
.
ЛЕКЦИЯ 4: «ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ»
Векторное произведение двух векторов
Определение. Векторным произведением вектора  на вектор
на вектор  называется новый вектор
называется новый вектор 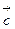 , обозначаемый символом
, обозначаемый символом
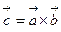
и определяемый следующими условиями:
1) модуль вектора 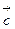 равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах  и
и  , т.е.
, т.е.
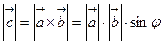 ,
,
где 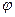 - угол между векторами
- угол между векторами  и
и  ;
;
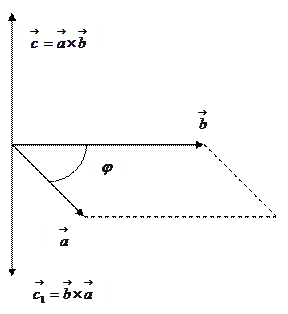 2) вектор
2) вектор 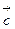 перпендикулярен к плоскости этого параллелограмма, т.е.
перпендикулярен к плоскости этого параллелограмма, т.е. 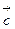 перпендикулярен
перпендикулярен  и
и 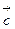 перпендикулярен
перпендикулярен  ;
;
3) вектор 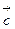 направлен в ту сторону от этой плоскости, с которой кратчайший поворот от вектора
направлен в ту сторону от этой плоскости, с которой кратчайший поворот от вектора  к вектору
к вектору  рассматривается совершающимся против часовой стрелки. Такое расположение векторов
рассматривается совершающимся против часовой стрелки. Такое расположение векторов  ,
,  и
и 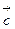 называется правой связкой.
называется правой связкой.
Свойства векторного произведения
1) Если векторы  и
и  коллинеарны, то
коллинеарны, то 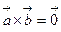 . В частности,
. В частности, 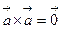 .
.
2) 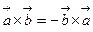
3) Распределительный закон: 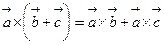 .
.
4) 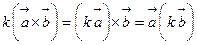
 Вычисление векторного произведения для векторов, заданных своими координатами
Вычисление векторного произведения для векторов, заданных своими координатами
Найдём векторные произведения ортов 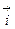 ,
, 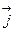 и
и 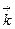 .
.
Получаем: 1) 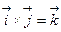 ; 2)
; 2) 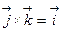 ; 3)
; 3) 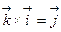 ;
;
4) 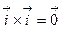 ; 5)
; 5) 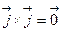 ; 6)
; 6) 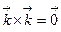 .
.
В результате получаем, что векторное произведение в последовательности 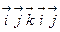 даёт следующий вектор со знаком «+», а в обратной последовательности – со знаком «–».
даёт следующий вектор со знаком «+», а в обратной последовательности – со знаком «–».
Пусть заданы векторы 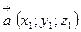 и
и 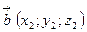 . Используя свойства векторного произведения, получаем:
. Используя свойства векторного произведения, получаем:
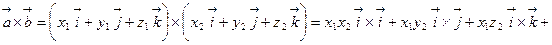
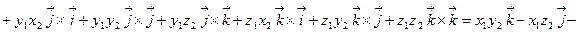
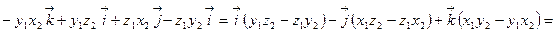
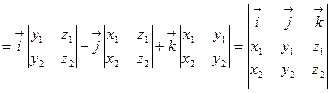
Таким образом,
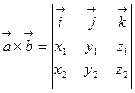 .
.
Вычисление площади треугольника с помощью векторного произведения.
Найдём площадь параллелограмма ABDC, построенного на векторах  и
и  .
.
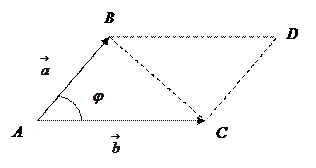
По определению векторного произведения
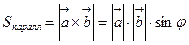 .
.
Тогда площадь треугольника ABC равна
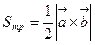 .
.
Пример: Вычислить площадь треугольника с вершинами 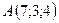 ,
, 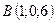 ,
, 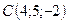 .
.
Найдём координаты векторов 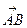 и
и 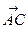 .
.
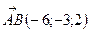 ,
, 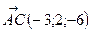
Вычислим векторное произведение 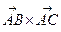 :
:
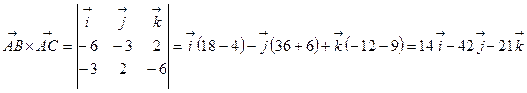 .
.
 Тогда
Тогда 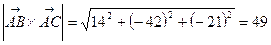 , следовательно, площадь треугольника ABC равна
, следовательно, площадь треугольника ABC равна











