Излучение при термодинамическом равновесии

Теория изучения плазмы значительно упрощается, если плазму рассматривать как замкнутый ансамбль. В этом случае плазма не обменивается энергией с внешним пространством; обмен энергией возможен только между частицами самой плазмы в результате их взаимодействия.

После такого обмена в плазме по истечении некоторого промежутка времени, величина которого зависит от концентрации частиц и их скоростей, установится равновесие, при котором средняя кинетическая энергия поступательного движения атомов, ионов и электронов будет одинакова и равна 3/2 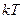. Такая плазма называется изотермической, или больцмановским излучателем.

Изолированная однородная плазма, находящаяся в термодинамическом равновесии при температуре Т и состоящая из идеального одноатомного газа, может быть описана следующими пятью соотношениями.

1. Давление р в плазме находится из уравнения состояния

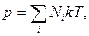(3.1)

где N_i: N_а , N_ион , N_е – концентрации (число частиц в единице объёма) атомов, ионов и электронов соответственно,

k – постоянная Больцмана.

2. Распределение частиц любого сорта i по скоростям v выражается функцией Максвелла:

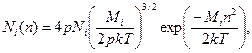(3.2)

где M_i – масса частиц;

N_i(n) – число частиц (концентрация), обладающих скоростями в пределах от n до n+dn;

N_i – концентрация, равная

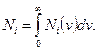(3.3)

3. Число атомов или ионов, находящихся в произвольном возбужденном состоянии k (заселенность состояния k), определяется формулой Больцмана:

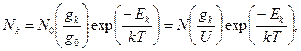(3.4)

где N₀ – заселенность основного состояния;

g₀ – статистический вес этого состояния;

g_k – статистический вес возбужденного состояния;

E_k – энергия возбужденного состояния, отсчитываемая от основного уровня. Суммы по состояниям ионов и атомов

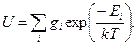(3.5)

где g_i – статистический вес верхнего электронного уровня

4. В случае однократной ионизации газа концентрации атомов, ионов и электронов связаны между собой формулой Саха:

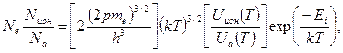(3.6)

где 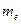- масса электрона;

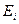– энергия ионизаци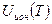и;

и 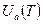- суммы по состояниям ионов и атомов;

g = 2 – статистический вес электронов.

5. Спектральная яркость излучения плазмы 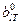в интервале длин волн от 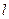до 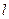+ 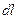находится по формуле Планка

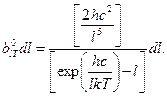(3.7)

В плазме, описываемой соотношениями (3.1) – (3.7), выполняются условия детального равновесия, состоящие в том, что оптические и ударные процессы возбуждения и девозбуждения каждого уровня в единице объема, происходящие в единицу времени, уравновешены. Излучение, возникающее в единице объема такой плазмы, полностью в нем же и поглощается: для данного излучения плазма оптически плотная.

В реальных случаях еще труднее удовлетворить формуле Планка, так как сам по себе процесс излучения во внешнее пространство – уже нарушение равновесия. Однако существуют источники излучения, условия в которых близки к условиям термодинамического равновесия, и излучение подчиняется формуле Планка в широкой области спектра.